7. Примеры дискретных распределений

1. Биномиальное распределение. Случайная величина , равная числу «УСПЕХОВ» в схеме Бернулли, имеет биномиальное распределение: , .

Математическое ожидание случайной величины, распределённой по биноминальному закону, равно

.

Дисперсия этого распределения равна .

2. Распределение Пуассона ,

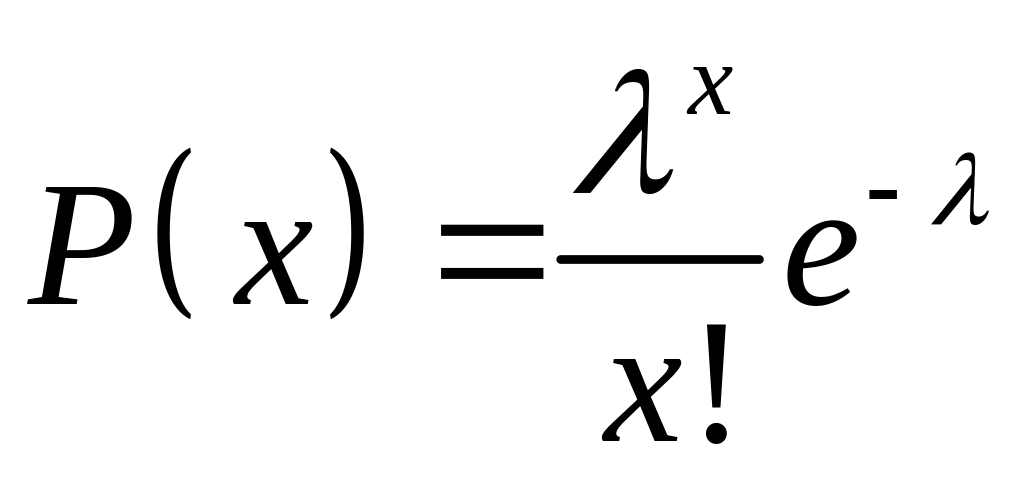Математическое ожидание и дисперсия случайной величины с распределением Пуассона , .

Распределение Пуассона часто используется, когда мы имеем дело с числом событий, появляющихся в промежутке времени или пространства, например: число машин, прибывших на автомойку в течении часа, число остановок станков в неделю, число дорожных происшествий и т.д.

3. Геометрическое распределение

Случайная величина имеет геометрическое распределение с параметром , если принимает значения с вероятностями . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха . Таблица распределения имеет вид:

8. Примеры непрерывных распределений

1. Равномерное распределение. Плотность равномерного или прямоугольного распределения:

,

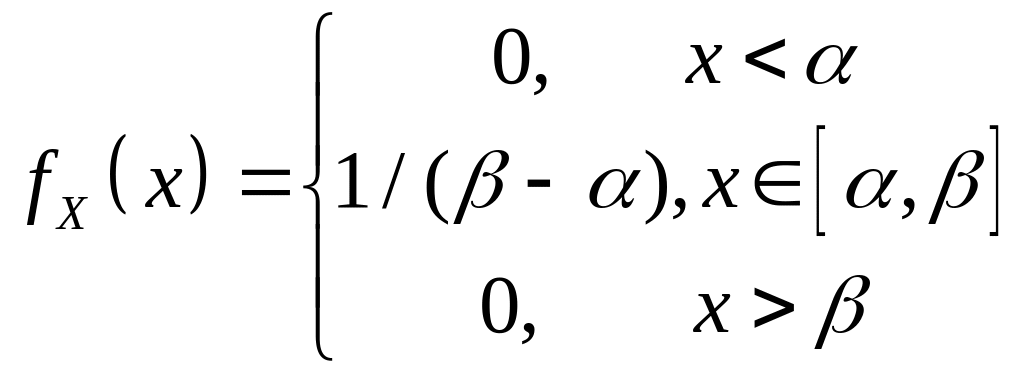т.е. вероятности всех возможных значений случайной величины одинаковы и равны .

Математическое ожидание случайной величины с равномерным распределением равно

,

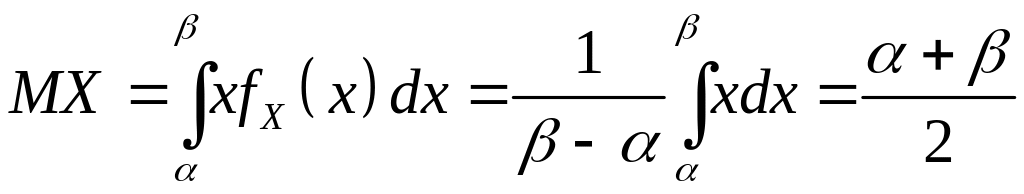дисперсия .

Функция распределения имеет вид 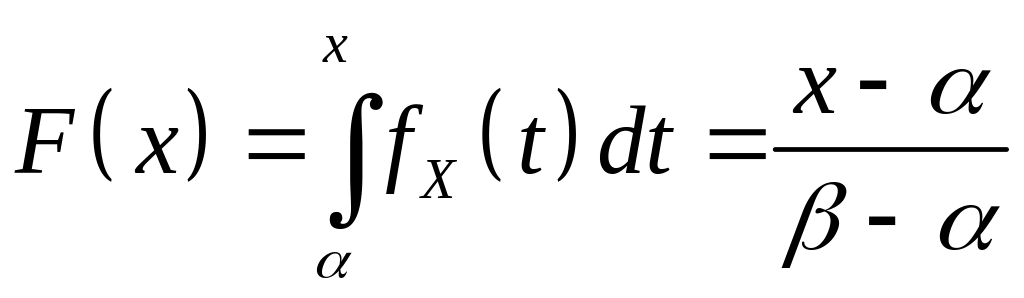, (Рисунок 3.5).

Рисунок 3.5. Графики плотности и функции равномерного распределения

2. Показательное (экспоненциальное) распределение  закон, функция плотности распределения которого имеет вид: 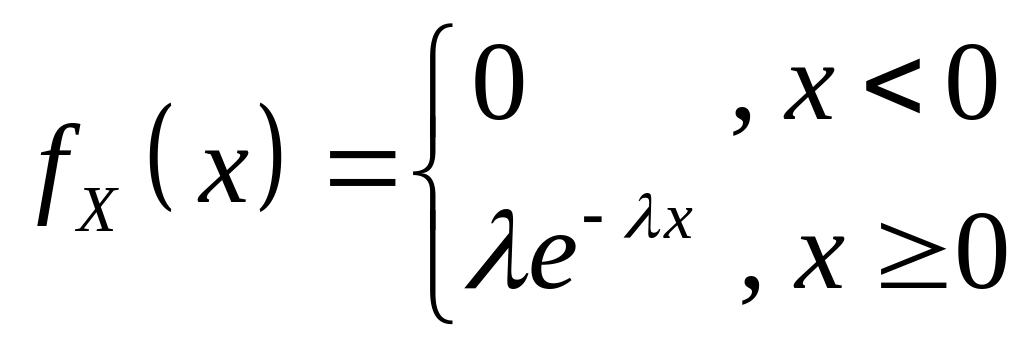, где параметр распределения 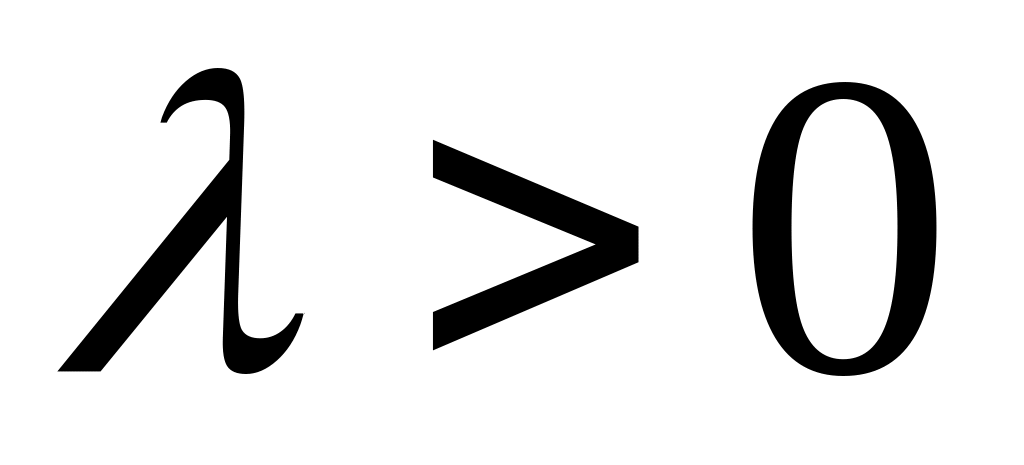есть действительное число (постоянный параметр) (Рисунок 3.6).

Функция распределения показательного закона имеет вид:

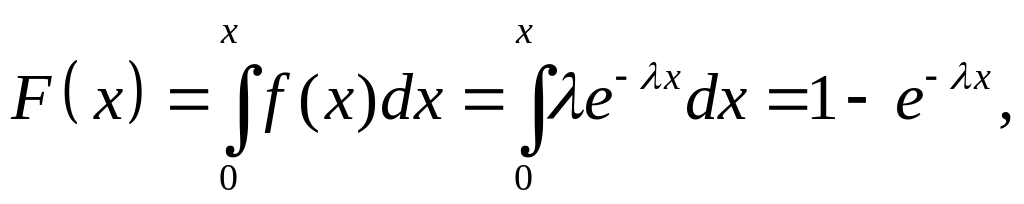
Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону, равны соответственно , .

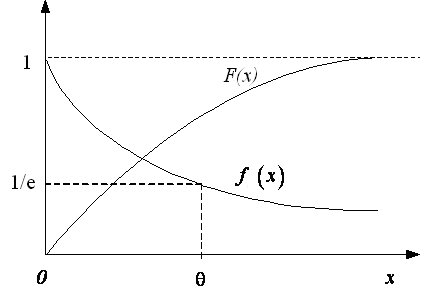
Рисунок 3.6. Графики плотности и функции показательного распределения

3. Нормальное распределение. Нормальный закон распределения вероятностей занимает особое место среди других законов распределения. В теории вероятности доказывается, что плотность вероятности суммы независимых или слабо зависимых, равномерно малых (т.е. играющих примерно одинаковую роль) слагаемых при неограниченном увеличении их числа как угодно близко приближается к нормальному закону распределению независимо от того, какие законы распределения имеют эти слагаемые (центральная предельная теорема А. М. Ляпунова).

Плотность вероятности нормально распределенной случайной величины имеет вид: , где и – вещественные параметры распределения, имеющие конечные значения, при этом часто используют обозначение .

Функция распределения записывается в виде

,

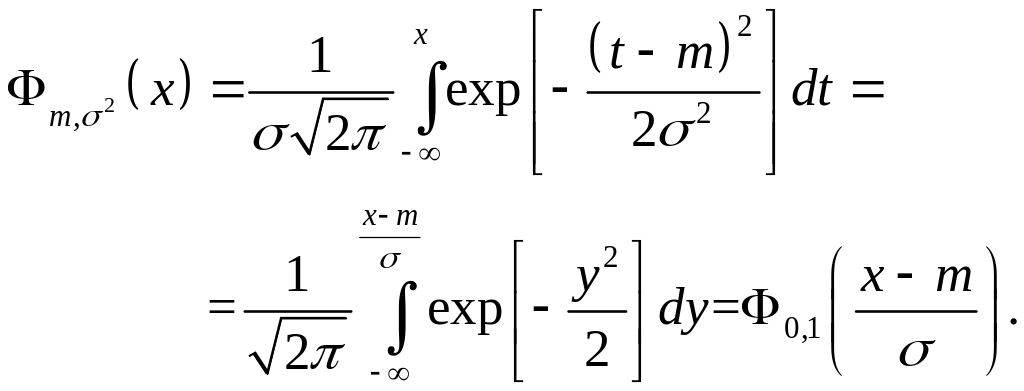Здесь – табулированный интеграл вероятности (значения интеграла можно найти во всех учебниках и задачниках по теории вероятностей). Функция и плотность нормального распределения изображены на Рисунок 3.7.

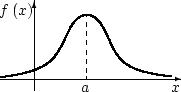
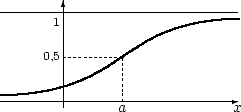
Рисунок 3.7. Графики плотности и функции нормального распределения

Математическое ожидание нормально распределенной случайной величины равно , дисперсия . Таким образом, параметры и имеют смысл математического ожидания и среднеквадратического значения (отклонения) случайной величины.

Распределение, описываемое функцией , называется нормальным или распределением Гаусса.

На Рисунок 3.8 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения .

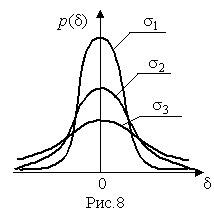
Рисунок 3.8. Кривые плотности нормального распределения, .

Из Рисунок 3.8 видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики – Муавр, Лаплас, Гаусс, Чебышев и Ляпунов.

Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Свойства нормального распределения.

А. Если случайная величина .

В. Если случайная величина то

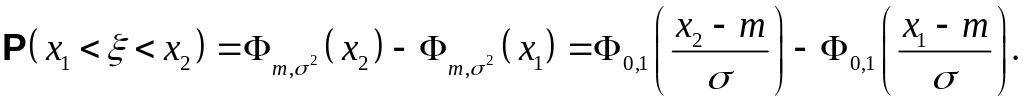
В частности, .

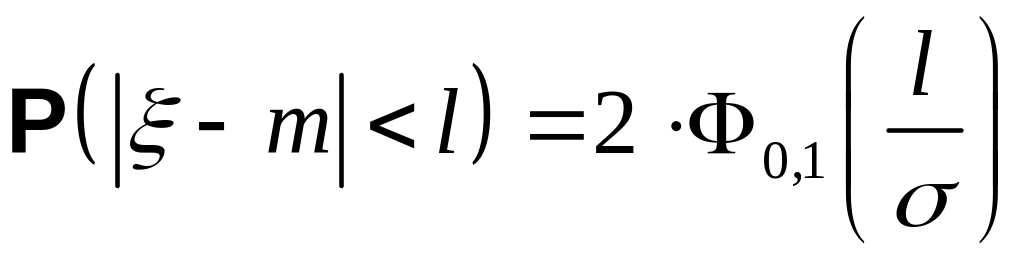Таким образом, вычисление любых вероятностей для нормально распределённой случайной величины сводится к вычислению функции распределения . Она обладает следующими свойствами:

С. Если , то для любого

D. Правило трех сигм. Если то

Большого смысла в запоминании числа 0.0027 нет, но полезно помнить, что почти вся масса нормального распределения сосредоточена в границах от до .

Пример 3.7. Дана случайная величина . Найти .

Решение. По формуле свойства В при получаем По таблице для функции Лапласа находим .

Пример 3.8. Случайная величина X – отклонение размера изделия от нормы – нормально распределенная, причём М (Х)= 0. Найти  (Х), если известно, что Р(– 3 < X < 3) = 0.7.

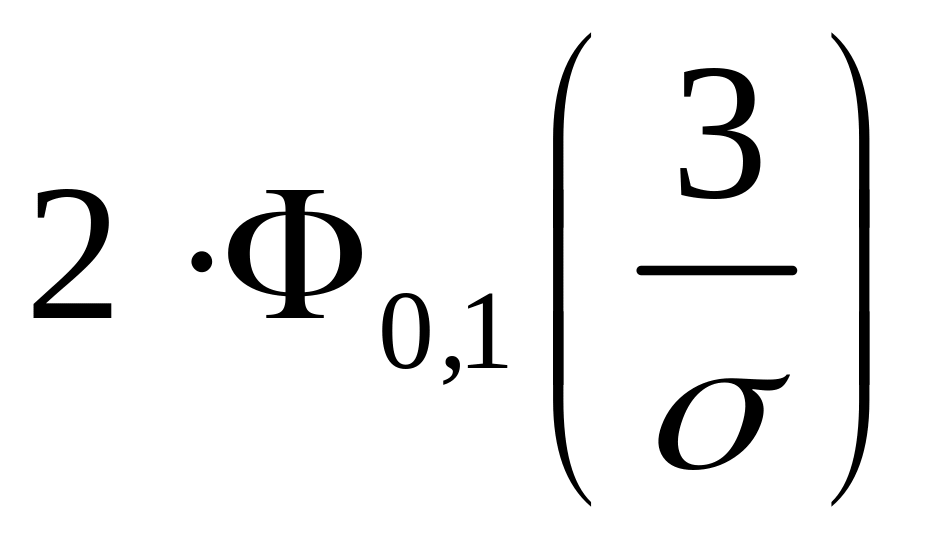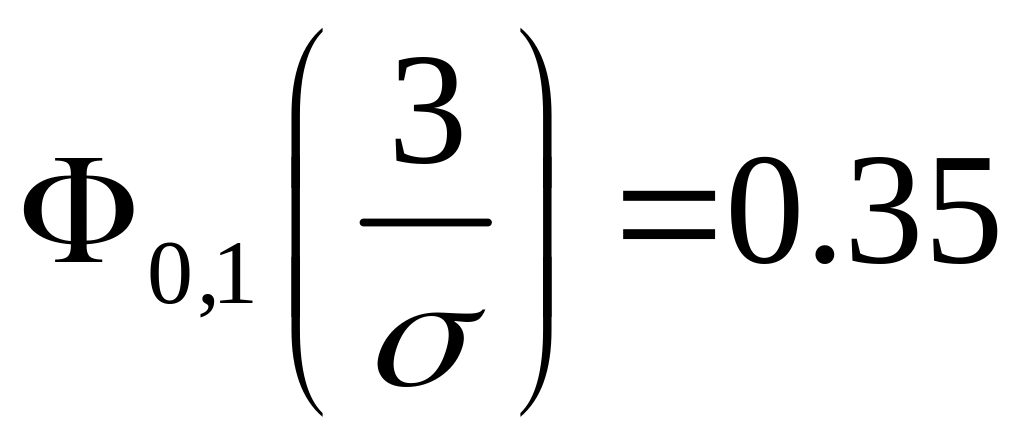Решение. Р(– 3 < X < 3) = Р( | X | < 3) = = 0.7. Отсюда следует, что , и, используя табличные данные (приложение 1), получаем 3/ =1.4, или  = 3/1.4  2.14.