12. Показательные неравенства. Общая схема решения.

1. В исходном неравенстве устанавливается область допустимых значений параметров, область определения. На области определения исходное неравенство приводится к виду

(1).

2. На множестве исследуется совокупность соответствующих особых частных неравенств типа Ø или типа ∞.

3. На множестве неравенство(1) для вспомогательной переменной равносильно системе

(2).

4. В неравенстве для каждого типа частных неравенств с общим решением

на множестве уравнения определяют подмножества значений размещения значения , нулей и точек разрыва функции . Неравенства определяют подмножества значений перестановки . В каждом из выделенных подмножеств

и

множества определяются общие решения системы (2).

5. На выделенном в п. 4 подмножестве значений параметров с общим решением находятся нули и точки разрыва функций , определяются множества значений их перестановок. На каждом из множеств значений перестановок нулей и точек разрыва функций с учетом значений находится множество решений каждой из систем

, …, как пересечение множеств решений неравенств системы.

6. На каждом выделенном в п.5 множестве значений перестановок нулей и точек разрыва функций находится множество решений совокупности систем объединением множеств решений всех систем. Полученные множества решений совокупности систем являются решением исходного неравенства на выделенном множестве значений параметров. Множества значений параметров с едиными общими решениями исходного неравенства определяют типы частных неравенств.

13. Логарифмические уравнения. Общая схема решения.

1. В искомом уравнении определяется область допустимых значений параметров, область определения задаётся некоторой системой неравенств.

2. На области определения исходное уравнение приводится к виду . Для вспомогательной переменной это уравнение равносильно уравнению .

3. Осуществляется решение уравнения на множестве допустимых значений параметров исходного уравнения. Для каждого из общих решений уравнения определяется область значений параметров.

4. Для каждого из общих решений на множестве проводится решение уравнения .

5. Для общих решений этого уравнения в множестве устанавливается подмножество значений параметров, для которых является решением уравнения и содержится в области определения исходного уравнения.

6. Всевозможные пересечения множеств для всех общих решений определяют все типы частных уравнений.

14. Логарифмические неравенства. Общая схема решения.

1. Логарифмические неравенства с параметрами , , и переменной определены на множестве всех упорядоченных значений 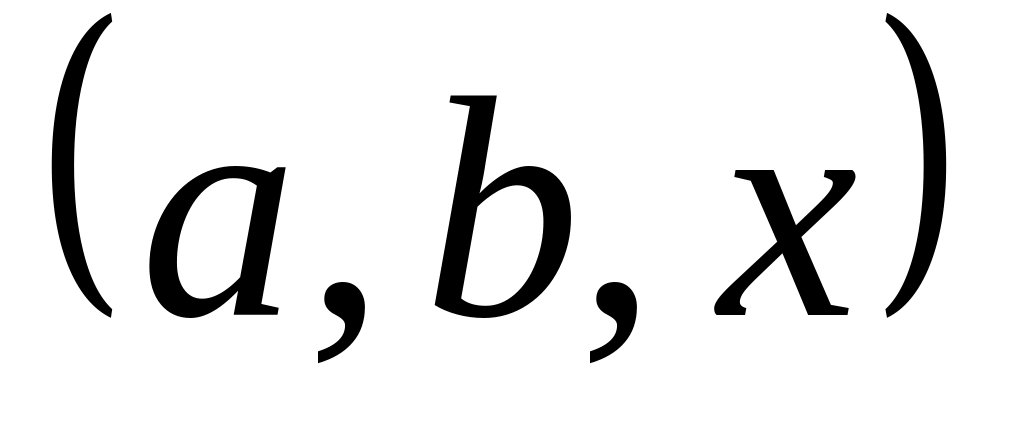, для которых основания , логарифмических выражений положительны и отличны от единицы, выражения ,…, 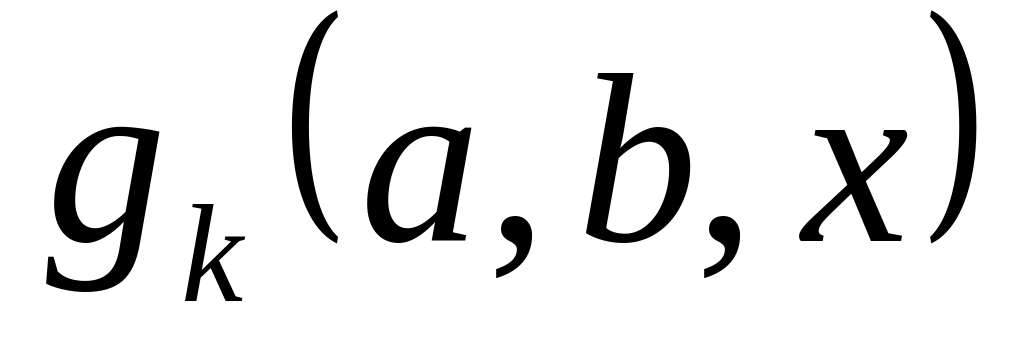под знаком логарифмов положительны. Исходя из этого область определения логарифмического неравенства определяется из системы

. (1)

Определяется разбиение области определения на подмножества и .

2. На области допустимых значений параметров исходное неравенство методом равносильных преобразований приводится к одному из следующих видов

(2)

(3)

(4)

(5).

3. На области допустимых значений параметров определяются граничные значения параметров системы (1). Для найденных граничных значений в исходном логарифмическом неравенстве соответствующие частные неравенства решаются отдельно. Устанавливаются нули и точки разрыва каждой из функций системы (1).

4. На области допустимых значений параметров исходного неравенства определяются граничные значения параметров уравнений

.

Для найденных граничных значений в исходном логарифмическом неравенстве соответствующие частные неравенства решаются отдельно.

Устанавливаются нули и точки разрыва каждой из функций для соответствующих неравенств вида (2)-(5).

5. На каждом из множеств и отдельно выделяют подмножества значений размещений, перестановок совокупности нулей и точек разрыва функций системы (1) неравенств (2)-(5).

На множестве значений определённого размещения или перестановки методом интервалов устанавливается общее решение системы (1) и соответствующего неравенства или общее решение системы (1) и одной из систем совокупностей

.

Выделенные промежутки являются общим решением некоторого неравенства на данном множестве значений параметров.

6. Множества значений параметров с одинаковыми общими решениями определяют типы частных неравенств с соответствующими характеристиками.