
- •8. Рациональные неравенства.
- •Общая схема решения.
- •9. Иррациональные уравнения.
- •Общая схема решения.
- •10. Иррациональные неравенства. Общая схема решения.
- •11. Показательные уравнения. Общая схема решения.
- •12. Показательные неравенства. Общая схема решения.
- •13. Логарифмические уравнения. Общая схема решения.
- •14. Логарифмические неравенства. Общая схема решения.
10. Иррациональные неравенства. Общая схема решения.
В исходном иррациональном неравенстве устанавливается область допустимых значений параметров и область определения.
На области определения неравенство при помощи равносильных преобразований приводится к неравенствам
 или
или
 ,
которые равносильны соответственно
системе
,
которые равносильны соответственно
системе
![]() ,
,
и совокупности
![]() .
.
Находятся граничные значения неравенств
 ,
,
 ,
,
 системы или совокупности, при этом
,
,
системы или совокупности, при этом
,
,
 -
либо рациональные выражения, либо
многочлены не выше
-
либо рациональные выражения, либо
многочлены не выше
 -ой
степени. Для каждого из граничных
значений параметров соответствующая
частная система неравенств решается
отдельно. Решение частных систем с
учётом области определения исходного
неравенства определяют решение исходного
частного неравенства.
-ой
степени. Для каждого из граничных
значений параметров соответствующая
частная система неравенств решается
отдельно. Решение частных систем с
учётом области определения исходного
неравенства определяют решение исходного
частного неравенства.На множестве остальных допустимых значений параметров определяются нули и точки разрыва функций: для -
 ,
для
-
,
для
-
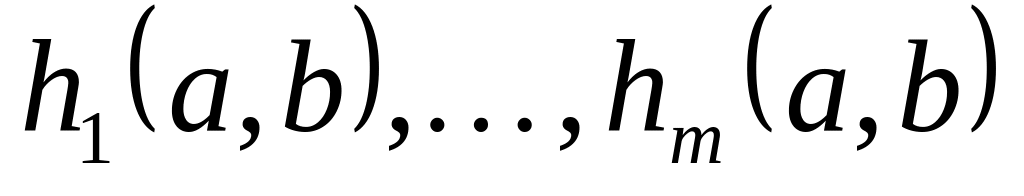 ,
для
-
,
для
-
 .
.
Для
выражений
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
совокупность
уравнений
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() определяют все значения параметров,
которым соответствуют размещения
определяют все значения параметров,
которым соответствуют размещения
![]() всех нулей и точек разрыва функций
,
,
.
всех нулей и точек разрыва функций
,
,
.
Для каждого из размещений множества всех нулей точек разрыва определяется соответствующее множество
 значений параметров. На
методом интервалов определяется
множество решений системы или
совокупности.
значений параметров. На
методом интервалов определяется
множество решений системы или
совокупности.Каждая из систем неравенств вида
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 определяет множество
значений некоторой перестановки нулей
и точек разрыва функций. На множестве
методом интервалов находится множество
решений системы или совокупности.
определяет множество
значений некоторой перестановки нулей
и точек разрыва функций. На множестве
методом интервалов находится множество
решений системы или совокупности.Все частные системы неравенств с одинаковыми общими решениями объединяются в типы с соответствующими характеристиками.
11. Показательные уравнения. Общая схема решения.
В исходном уравнении определяется область допустимых значений параметров, устанавливается область определения уравнения. На области определения исходное уравнение приводится к виду
![]() (1).
(1).
На множестве
 исследуется совокупность соответствующих
особых частных уравнений типа Ø или
типа ∞.
исследуется совокупность соответствующих
особых частных уравнений типа Ø или
типа ∞.На множестве
 уравнение (1) для вспомогательной
переменной
уравнение (1) для вспомогательной
переменной
 равносильно системе
равносильно системе
![]() .
.
.
.
Осуществляется решение уравнения
 на множестве допустимых значений
параметров искомого уравнения, для
которых
на множестве допустимых значений
параметров искомого уравнения, для
которых
 .
Для каждого из общих решений
.
Для каждого из общих решений
 уравнения
на множестве
уравнения
на множестве
 выделяются
подмножества
выделяются
подмножества
 всех значений параметров, для которых
всех значений параметров, для которых
 .
.Для каждого из общих решений уравнения на множестве осуществляется решение уравнения
 .
Для общих уравнений
.
Для общих уравнений
 этого уравнения на множестве
устанавливается подмножество
этого уравнения на множестве
устанавливается подмножество
 значений
параметров, для которых
является общим решением уравнения
и, следовательно, уравнения
.
значений
параметров, для которых
является общим решением уравнения
и, следовательно, уравнения
.На области определения исходного уравнения всевозможные пересечения множеств для всех общих решений уравнений вида определяют все типы частных уравнений.
