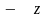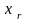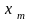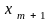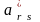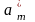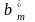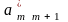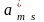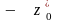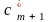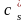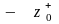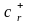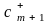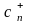2. Симплекс – метод при заданном начальном допустимом базисном решении

Идея метода: Аналитически из системы ограничений определяется одна из вершин многогранника решений и осуществляется последовательный переход к таким его соседним вершинам, каждая из которых ближе к оптимальному решению, чем предыдущая.

Он непосредственно применяется к общей задаче линейного программирования в стандартной форме:

Минимизировать 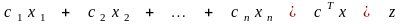(2.1)

при ограничениях 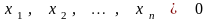, т. е. , (2.2)

,

. . . . . . . . . . . . . . . . . . . . . . (2.3)

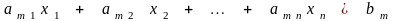
т. е. ; ,

причем предполагается, что имеется базисное допустимое решение, удовлетворяющее всем ограничениям.

Базисное решение, удовлетворяющее ограничениям, можно получить, если найти столбцов матрицы , образующих несингулярную матрицу 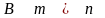. Если эти столбцы соответствуют переменным 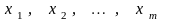, то ограничения могут быть преобразованы так, чтобы выразить через 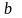и остальные , что можно записать в виде

,

,

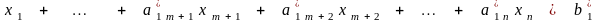. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2.4)

.

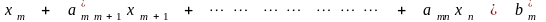Если умножить ограничения системы (2.4) на и вычесть из , то исключатся из и мы получим

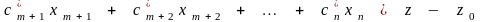, (2.5)

где .

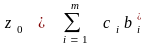Разумеется, уравнения (2.4) и (2.3) выражают одинаковые ограничения, а уравнения (2.5) и (2.1) представляют одну и ту же целевую функцию, хотя и в разных алгебраических формах. Уравнения (2.4) и (2.5) являются канонической формой для базиса . Если положить 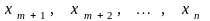равными 0, то соотношения

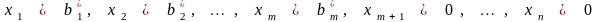
задают базисное решение. Если все 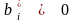, это решение допустимо. Среди таких решений надо найти оптимальное. Симплекс-метод обеспечивает систематическую процедуру для такой замены одной допустимой канонической формы на другую, при которой значение целевой функции уменьшается.

Применим процедуру симплекс – метода к рассмотренному и решенному графически примеру максимизации прибыли при производстве полок.

В стандартной форме с неотрицательными дополнительными переменными и ограничения и целевая функция принимают вид

,

, (2.11)

.

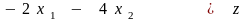Поскольку в этом случае коэффициенты положительны, а новые переменные имеют коэффициент +1, ясно, что набор 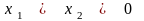, , 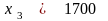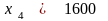образует базисное фундаментальное решение, а уравнения (2.11) имеют соответствующий вид.

Функция , имеющая нулевое значение, выражена через небазисные переменные, которые также имеют нулевое значение. Как в таком случае можно уменьшить значение функции ? Поскольку и должны быть неотрицательны, их можно только увеличивать. Поскольку коэффициенты при и в канонической форме функции отрицательны, увеличение и приведет к убыванию функции . Для простоты выберем одну из переменных. Так как коэффициент при больше по модулю, выбираем .

Однако при увеличении значения и будут изменяться, поскольку должны выполняться уравнения (2.11). Все переменные при этом должны оставаться неотрицательными. Таким образом, должен существовать предел увеличения .

Поскольку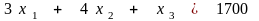 , обращается в 0 при = 1700/4 = 425.

Поскольку 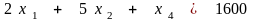, обращается в 0 при = 1600/5 = = 320.

Таким образом, мы не можем увеличивать более чем до 320 (минимального из этих значений), не нарушая условие неотрицательности.

Второе ограничение может быть записано в виде

.

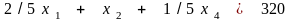Если вычесть это уравнение, умноженное на 4, из уравнения (2.11) (4 - коэффициент при в этом уравнении), а затем вычесть это же уравнение, умноженное на - 4, из выражения для целевой функции (- 4 - коэффициент при в целевой функции), то переменная будет исключена отовсюду, кроме второго ограничения, куда она входит с коэффициентом 1. Ограничения и целевая функция принимают вид

,

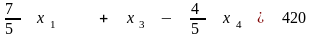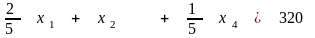, (2.12)

,

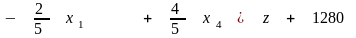что является канонической формой для базиса , , представляющего базисное допустимое решение.

Небазисными переменными стали переменные и . В данный момент они равны 0. Теперь можно уменьшить значение функции , увеличив только . Но на сколько можно увеличить 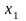, чтобы и оставались неотрицательными?

Для уравнения

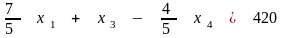
обращается в 0 при .

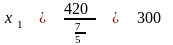Для уравнения

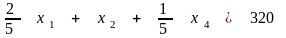
обращается в 0 при .

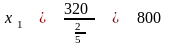Таким образом, нельзя увеличивать , более чем до 300 (минимального из этих значений). После деления на 7/5 (коэффициент при ) первое ограничение принимает вид

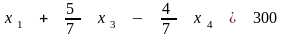
Исключим из другого ограничения и выражения для целевой функции, вычтя последнее соотношение, умноженное на 2/5 и -2/5, из ограничения и целевой функции. Получим каноническую форму задачи в базисе , , тоже являющимся допустимым. Она имеет следующий вид:

,

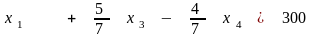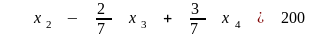, (2.13)

.

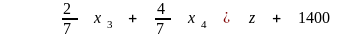Заметим, что увеличение любой из небазисных переменных , (эти переменные входят в выражение для целевой функции с положительными коэффициентами) приведет к возрастанию функции . Таким образом, дальнейшее убывание функции невозможно и достигнуто минимальное значение функции , равное -1400 при допустимом базисном решении = 300, = 200, = = 0. Если вернуться к геометрической интерпретации на рис.. 1.1, то можно убедиться, что последовательность канонических форм привела из точки 0 в точку и из точки в точку 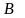- точку минимума. Заметим, что при выборе в уравнениях (2.11) увеличения та же процедура привела бы из точки 0 в точку через точку .

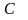Этот итерационный процесс удобно проиллюстрировать в так называемых симплекс-таблицах. Они состоят из уравнений (2.11) - (2.13) для ограничений и целевой функции, записанных в виде

;

;

.

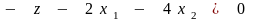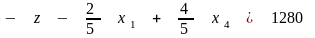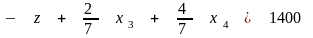Ниже приведены три таблицы.

Итерация	Базис	Значение
0		1700	3	4	1	.
		1600	2	5*	.	1
		0	-2	-4	.	.
1		420	7/5*	.	1	-4/5
		320	2/5	1	.	1/5
		1280	-2/5	.	.	4/5
2		300	1	.	5/7	-4/7
		200	.	1	-2/7	3/7
		1400	.	.	2/7	4/7

На итерации 0 звездочкой отмечено значение 5 - коэффициент при переменной, которую мы собираемся обратить в базисную в предельном ограничении. На итерации 1 отмечено число 7/5. Заметим также, что мы ставим точки вместо переменных, обязанных иметь нулевые значения, чтобы отличить их от переменных, обращающихся в 0 случайно.

Результаты, полученные в рассмотренном примере, можно обобщить. Предположим, что начальная каноническая форма задана, и что на -й итерации получена каноническая форма, заданная уравнениями (2.4) и (2.5), запись которых приведена ниже в таблице.

Итерация	Базис	Значе-ние
k			1	.	.	.		.
			.	1	.	.		.
			.	.	.	.		.
			.	.	.	1		.
			.	.	.	.		.			-
			.	.	.	.		1
			.	.	.	.		.

Итерационный процесс состоит из трех шагов.

1. Найти переменную для включения в базис.

Переменные 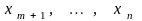являются небазисными. Находим наименьший из коэффициентов 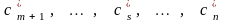. Пусть это коэффициент . Если коэффициент отрицателен, то увеличение приведет к убыванию функции . В связи с этим принимается соглашение, что если некоторые коэффициенты 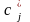- отрицательны, то из них следует выбрать наибольший по модулю коэффициент. Это разумно, но несущественно, поскольку подходит любое отрицательное значение . Если все 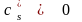, то значение функции не может быть уменьшено, и минимум найден.

2. Найти переменную для исключения из базиса.

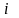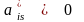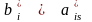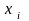Насколько можно увеличивать , не нарушая условия неотрицательности текущих базисных переменных? Если в -м ограничении , то наибольшее значение, которое может принимать переменная , равно , иначе переменная станет отрицательна. (Если 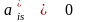, то при увеличении базисная переменная будет возрастать.) Таким образом может увеличиваться до значения

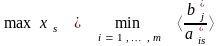, (2.14)

Если этот минимум достигается в строке , то обращается в 0, когда принимает значение 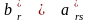. Другие базисные переменные останутся неотрицательными. Элемент 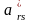называется ведущим элементом, строка - ведущей строкой, а столбец 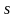- ведущим столбцом.

3. Построить новую каноническую форму.

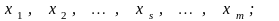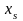Теперь новый базис и переменная стала базисной. Чтобы построить новую каноническую форму, коэффициент при в ведущей строке сделаем равным 1, поделив строку на , чтобы образовать новую ведущую строку.

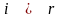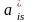Затем удалим из других ограничений целевой функции. Для этого из -строки ( ) с коэффициентом при вычтем (новая ведущая строка). Чтобы преобразовать целевую функцию с коэффициентом 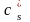(< 0) при , вычтем (новая ведущая строка) из строки, соответствующей целевой функции.

На очередной итерации каноническая форма будет выглядеть следующим образом:

Итерация	Базис	Значе-ние
k+1			1	.	.			.			.
			.	1	.			.			.
			.	.	.			.			.
			.	.	.			.			1
			.	.	.			.			.
			.	.	.			1			.
			.	.	.			.			.

где

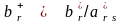; (2.15)

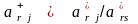; (2.16)

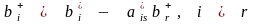; (2.17)

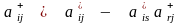; (2.18)

; (2.19)

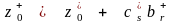. (2.20)

Формулы (2.15) - (2.20) приведены для дальнейших ссылок. Вычисления удобнее выполнять в соответствии с шагом 3.

Теперь, построив новую каноническую форму, необходимо вернуться к шагу 1 и выбрать минимальное из чисел 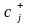. В конце концов мы обнаружим,

что все они положительны, следовательно, минимум функции z достигнут.