3. Некоторые определения из линейной алгебры

Отрезок , где и 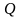- две точки, представленные векторам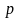и и 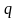, состоит из точек, определяемых соотношением

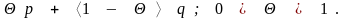
Точечное множество 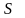называется выпуклым, если для любых точек и этого множества весь отрезок содержится в множестве .

Экстремальной точкой (вершиной или углом) выпуклого множества называется любая точка, не лежащая внутри произвольного отрезка, соединяющего разные точки множества.

Выпуклой оболочкой точек 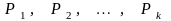, представленных векторами , называется множество точек вида

,

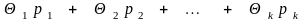где 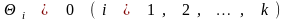и

Н

а)

а рис. 1.6, а изображено выпуклое множество. Множество, изображенное на рис. 1.6, б не является выпуклым – некоторые точки отрезка не принадлежат ему.

а) б)

Рис. 1.6

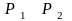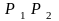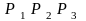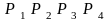Точки являются вершинами первого множества. Выпуклая оболочка двух точек есть отрезок . Выпуклая оболочка трех точек – треугольник , четырех – тетраэдр , а пяти точек - гипермногогранник с вершинами в этих пяти точках.

3. Основные результаты линейного программирования

Утверждение 1. Если ограничения имеют допустимое решение, то они имеют и базисное решение.

Докажем это, построив базисное допустимое решение. Пусть в допустимом решении переменных равны 0, а остальные положительны. Тогда без потери общности

,

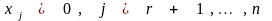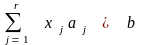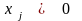, где для 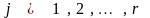, (1.13)

а 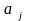- столбцы матрицы .

Если - линейно независимы, то 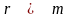- ранг матрицы и решение является базисным допустимым решением (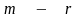 базисных переменных равны 0).

Если 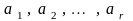линейно зависимы, то

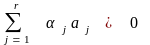, где не все 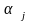равны 0 или отрицательны (1.14)

(при необходи+мости это равенство может быть умножено на -1).

Пусть ,

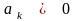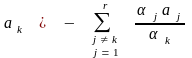, (1.15)

тогда

.

Если выбрать так, что

,

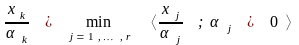то значения

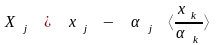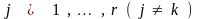, , (1.16)

₊, ,

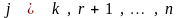неотрицательны и поэтому являются допустимыми решениями, в которых по крайней мере 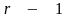переменная имеет строго положительное значение. Следовательно, количество строго положительных переменных уменьшено на одну переменную. Продолжая рассуждения таким же образом, в конце концов придем к ситуации, при которой 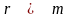, т.e. получим базисное допустимое решение.

Утверждение 2. Допустимая область является выпуклым множеством.

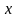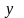Если и принадлежат допустимой области и 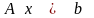, , 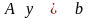причем , , тогда, если

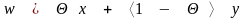, где , то .

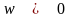Следовательно,

.

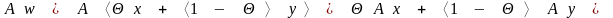
Таким образом, 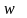принадлежит допустимой области, значит, доказано, что допустимая область является выпуклым множеством.

Утверждение 3. Базисные допустимые решения соответствуют вершинам выпуклого множества

Пусть 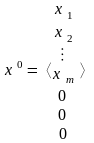- базисное допустимое решение.

Тогда 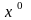является единственным решением уравнения , где , причем последние 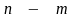координат вектора равны 0.

Если - не вершина, то можно найти две другие точк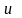и и 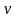, такие что 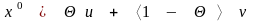для некоторого 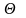, причем 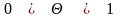и выполнены условия 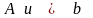, , 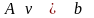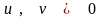. Таким образом, для последних координат имеем

. . . . . . . . . . . . . . . .

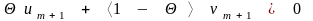
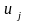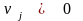
Но поскольку , , и 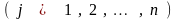, система равенств

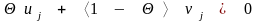
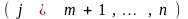
имеет решение только в случа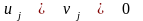е , где .

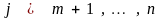Таким образом, , - базисные допустимые решения, обращающиеся в 0 в тех же точках, что и . Поэтому из единственности решения следует, что = = , что противоречит выбору и . Поэтому каждое базисное допустимое решение - вершина.

Можно доказать и обратное, т. е. что все вершины соответствуют: базисным допустимым решениям.

Пусть - вершина допустимой области. Пусть 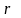координат строго положительны. Покажем, что не превосходит 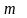, т. е. - базисное допустимое решение. Пусть 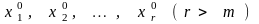положительны. Пусть 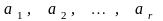- соответствующие столбцы матрицы 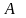; предположим, что они линейно зависимы.

Как и при доказательстве утверждения 1, найдем такие , не все равные 0, что

.

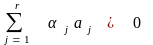Легко видеть, ч

то если

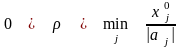для ,

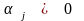то векторы

,

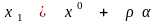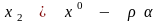
где

,

удовлетворяют условию , .

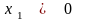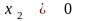Поскольку 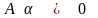, то

.

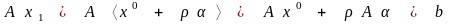Аналогично .

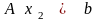Таким образом, и - допустимые решения и 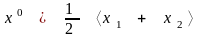. Следовательно, - не вершина, а это противоречит выбору , значит, не превосходит .

Если заданы

ограничений на переменных, то имеется самое большее 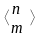базисных допустимых решений (или вершин) и их выпуклая оболочка образует допустимую область.

Утверждение 4. Если целевая функция имеет конечный минимум, то, по крайней мере, одно оптимальное решение является базисным.

Пусть допустимые базисные решения соответствуют точкам векторов , и пусть целевая функция принимает в этих точках значения .

Если 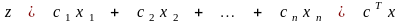, то 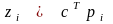для 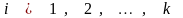. Для любой другой точки в допустимой области

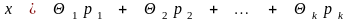, где , ,

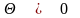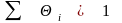значение функции в этой точке

.

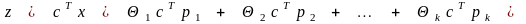
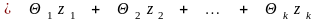Таким образом, нахождение в выпуклой оболочке точек точки , в которой функция достигает минимума, сводится к задаче нахождения чисел 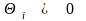, удовлетворяющих условию 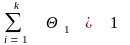и минимизирующих функцию .

Среди значений имеется минимальное (их может быть несколько). Пусть 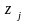такое значение, т. е. 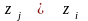для .

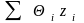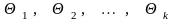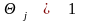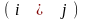Величина , являющаяся взвешенной средней величин , с весами , будет минимальна при и . Итак, минимум функции достигается в вершине .

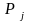Полученные результаты означают, что при поиске оптимального решения в допустимой области можно ограничиться базисными допустимыми решениями. Симплекс-метод представляет собой процедуру получения такого решения.