1.2. Графическое решение двумерных задач
На примере 1 мы показали, каким образом задачи ЛП возникают на практике, и продемонстрировали графический метод их решения. Рассмотрим еще несколько простых примеров, чтобы выявить несколько общих свойств задач ЛП, которые могут подсказать путь к их общему решению.
Пример 1
Минимизировать функцию
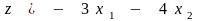
при
ограничениях
,
,
,
.
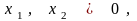
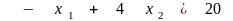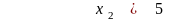Допустимой областью, изображенной на рис. 1.2, является четырехугольник PQRS.
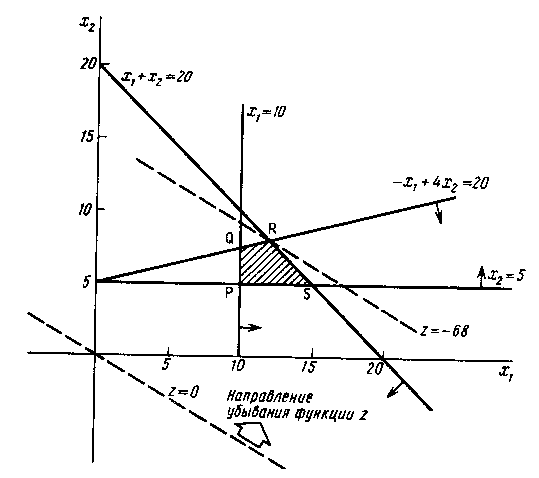
Рис. 1.2
Два
последних ограничения усиливают условия
неотрицательности. Функция
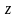убывает
в направлении вектора
.
Минимальное
значение функции
= – 68 и достигается в точке
=
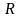(12, 8). Заметим, что, как и в примере 1,
минимум достигается в вершине допустимой
области. Оптимальным решением задачи
является точках
= 12,
=
8 с минимальным значением функции
= – 68.
Иногда задача имеет более чем одно оптимальное решение.
Пример 2
Минимизировать
функцию
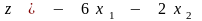
при ограничениях
,
.
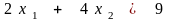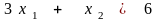На рис.
1.3 четырехугольник ОАВС изображает
допустимую область
,
,
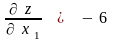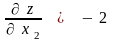и, таким образом, вектор
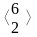указывает
направление убывания функции
.
Любая точка на отрезке ВС является
оптимальным решением. В частности, в
вершинах В =
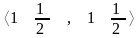и С = (2, 0) достигаются оптимальные решения,
соответствующие одному и тому же
минимальному значению функции
=
– 12.
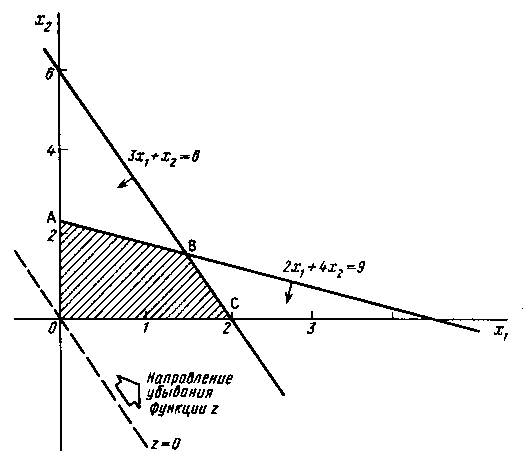
Рис. 1.3
Любая точка на отрезке ВС представляется формулой
,
где
.
Для каждой такой точки значение функции равно
.
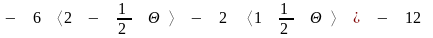Функция
имеет единственное
минимальное
значение.
Иногда решение задачи не ограничено.
Пример 3
Максимизировать
функцию
при ограничениях
,
.
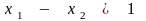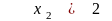Допустимая область, изображенная на рис. 1.4, не ограничена в направлении, в котором функция возрастает, т. е. в допустимой области не существует конечной точки, в которой функция достигала бы максимума.
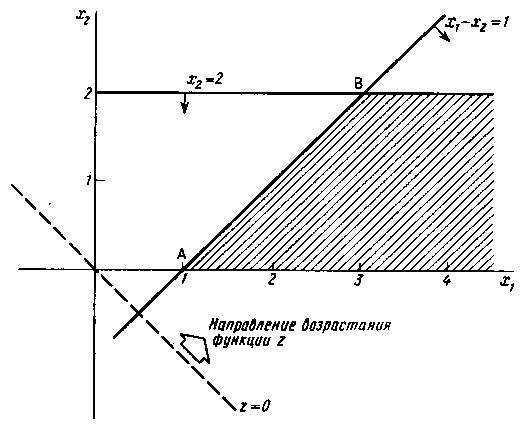
Рис. 1.4
Решение,
как и максимальное значение функции
,
не ограничено. Однако некоторые задачи
с неограниченными допустимыми областями
имеют конечные решения. Например, задача
максимизации функции
при
ограничениях из примера 3 имеет конечное
решение.
Разумеется,
если бы задача состояла в минимизации
функции
при
тех же ограничениях, то минимум достигался
бы в единственной точке
(min)
= 1 в вершине допустимой области (
=
1,
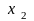= 0).
Иногда задача не имеет решения, поскольку допустимой области не существует.
Пример 4
Минимизировать
функцию
при ограничениях
,
.
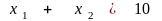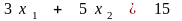Ограничения задачи противоречивы, поэтому нет допустимых решений (рис. 1.5).
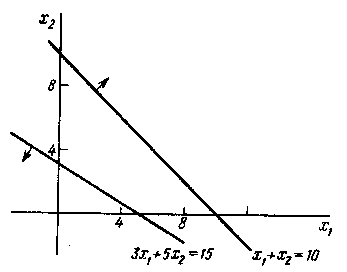
Рис.1.6
Уже из рассмотренных выше примеров можно вывести несколько характерных черт задач линейного программирования. Во-первых, допустимая область всегда является выпуклым многоугольником, даже в случае, когда она не ограничена. Во-вторых, оптимальное решение всегда достигается в вершинах допустимой области. В примере 2 и вершина В, и вершина С являются оптимальными точками. Эти результаты могут быть обобщены.