
Чертов А.Г., Воробьев А.А. Задачник по физике / Ответы / Ответы / Ответы
.doc
12.59.
1)
![]() =
= ![]() gd2/(18η2) =
6,71 мм/с
(ρ1
и
ρ2 –
плотность латуни
и глицерина; η – динамическая
вязкость глицерина); 2) обтекание шарика
ламинарное.
12.60.
gd2/(18η2) =
6,71 мм/с
(ρ1
и
ρ2 –
плотность латуни
и глицерина; η – динамическая
вязкость глицерина); 2) обтекание шарика
ламинарное.
12.60.
![]() 2 =
2 = ![]()
![]()
![]() =
27,7 см/с
(ρ2
и
=
27,7 см/с
(ρ2
и
![]() – плотность
и
динамическая вязкость касторового
масла; (ρ2
и η – те
же величины для глицерина).
– плотность
и
динамическая вязкость касторового
масла; (ρ2
и η – те
же величины для глицерина).

1
 3.1.
9 ГН.
13.2.
3.1.
9 ГН.
13.2.
![]() =
50,1 нКл. 13.3.
ε =
=
50,1 нКл. 13.3.
ε = ![]() =
2.
13.4. Q =
=
2.
13.4. Q =
![]() =
86,7 фКл.
13.5.
=
86,7 фКл.
13.5.
![]() =
219 км/с;
=
219 км/с;
![]() =
6,59∙1014 c-:l
(m – масса
электрона; е – его
заряд). 13.6.
=
6,59∙1014 c-:l
(m – масса
электрона; е – его
заряд). 13.6.
![]() =
287 мН. 13.7.
F =
=
=
287 мН. 13.7.
F =
= ![]() =54 мН.
13.8.
=54 мН.
13.8.
![]() =
= 0,14 мкКл;
Q2 =
=
= 0,14 мкКл;
Q2 = ![]() =
20 нКл.
13.9.
0,09 мкКл; – 0,01 мкКл.
13.10.
Mежду зарядами на расстоянии x = 40 см
от
заряда 4
=
20 нКл.
13.9.
0,09 мкКл; – 0,01 мкКл.
13.10.
Mежду зарядами на расстоянии x = 40 см
от
заряда 4![]() ;
положительный.
13.11.
Точка находится на расстоянии l1 =
20 см
от
заряда Q1; – 8∙10–8 Кл;
неустойчивое.
13.12.
Q =
;
положительный.
13.11.
Точка находится на расстоянии l1 =
20 см
от
заряда Q1; – 8∙10–8 Кл;
неустойчивое.
13.12.
Q =
![]() =
= ‑ 0,577 нКл;
не будет устойчивым.
13.13.
Q1
=
= ‑ 0,577 нКл;
не будет устойчивым.
13.13.
Q1![]() Q= –287 нКл.
13.14.
Q= –287 нКл.
13.14.
![]() =
1,5 мН.
13.15.
F =
=
1,5 мН.
13.15.
F = ![]() τ/(4πε0α) = 4,5 мН.
13.16.
F =
=
τ/(4πε0α) = 4,5 мН.
13.16.
F =
= ![]() (4πε0α) =
6,37 мН.
13.17.
F =
(4πε0α) =
6,37 мН.
13.17.
F = ![]() =
= 1,27 мкН.
13.18.
9 мН. 13.19.
=
= 1,27 мкН.
13.18.
9 мН. 13.19.![]() =4,03 мН.
13.20.
1)
F1 =
=
=4,03 мН.
13.20.
1)
F1 =
=  = 0,16 мН;
2)F2 = QQ1/(4πε0l22) =
= 2,25 мкН.
13.21.
F = Qr
/(2πε0R)
=
З,6 мН.
13.22.
F = Qτ/(4πε0R)
= 35 мкН.
= 0,16 мН;
2)F2 = QQ1/(4πε0l22) =
= 2,25 мкН.
13.21.
F = Qr
/(2πε0R)
=
З,6 мН.
13.22.
F = Qτ/(4πε0R)
= 35 мкН.
14.1.
4,09 кВ/м.
14.2.
2,99 кВ/м;
607 В/м.
14.3.
280 В/м.
14.4.
6 см;12 см.
14.5.
За отрицательным зарядом на расстоянии
d1
= d![]() 14.6.
34 кВ/м. 14.7.
E = = 2,71 кВ/м.
Решение.
Из рис. 6 следует, что элемент заряда
dQ,находящийся
на элементе dl,
создает
напряженность
dE =
14.6.
34 кВ/м. 14.7.
E = = 2,71 кВ/м.
Решение.
Из рис. 6 следует, что элемент заряда
dQ,находящийся
на элементе dl,
создает
напряженность
dE = ![]() ,
или
dE =
,
или
dE = ![]() Разложим
dE
на
две составляющие: dE1
–
по нормали к плоскости
кольца и dE2
–
параллельно ей – и просуммируем
эти составляющие для всех элементов
кольца. При этом составляющие, параллельные
плоскости кольца, в сумме дадут нуль.
Сумма вертикальных
составляющих выразится интегралом
Разложим
dE
на
две составляющие: dE1
–
по нормали к плоскости
кольца и dE2
–
параллельно ей – и просуммируем
эти составляющие для всех элементов
кольца. При этом составляющие, параллельные
плоскости кольца, в сумме дадут нуль.
Сумма вертикальных
составляющих выразится интегралом
![]() Выражая
Выражая![]() через
r b R, получим
после интегрирования
окончательную
через
r b R, получим
после интегрирования
окончательную

14.8.
E = σ/(4ε0) = 28,3 В/м.
Решение.
Полусферу
разобьем на дифференциально
тонкие кольца (рис. 7) с зарядом
dQ = σdS = 2![]() rσR
rσR![]() ,тогда
напряженность
dE,
создаваемая
таким
кольцом
в
центре полусферы, dE =
,тогда
напряженность
dE,
создаваемая
таким
кольцом
в
центре полусферы, dE = ![]()
![]() (см.
задачу 14.7).
(см.
задачу 14.7).
Учитывая,
что
r = Rsin![]() и
a = Rcosφ,
после
интегрирования
получим
Е =
и
a = Rcosφ,
после
интегрирования
получим
Е =  cosφd
cosφd![]() =
= ![]() .
14.9.
1) 0; 2)
900 В/м;
3)
400 В/м; график см. на рис. 8. 14.10.
E1 = 0;
E2 =
.
14.9.
1) 0; 2)
900 В/м;
3)
400 В/м; график см. на рис. 8. 14.10.
E1 = 0;
E2 = ![]() = 1,11кВ/м;
E3 =
= 1,11кВ/м;
E3 =
![]() =
200 В/м;
график
см. на рис. 9. 14.11.
5,55 нКл/м. 14.12.
43,2 МВ/м.
14.13.
64,3 кВ/м. 14.14.
E1 = 0;
E2 =
=
200 В/м;
график
см. на рис. 9. 14.11.
5,55 нКл/м. 14.12.
43,2 МВ/м.
14.13.
64,3 кВ/м. 14.14.
E1 = 0;
E2 = ![]() = 75,5 В/м;
график
см.
на
рис.10. 14.15.
E1 = 0;
E2 =
= 75,5 В/м;
график
см.
на
рис.10. 14.15.
E1 = 0;
E2 =
![]() =
=
=
= 200 В/м;
E3 =
200 В/м;
E3 = ![]() = 180Β/м,
график
см. на рис. 11.
= 180Β/м,
график
см. на рис. 11.
1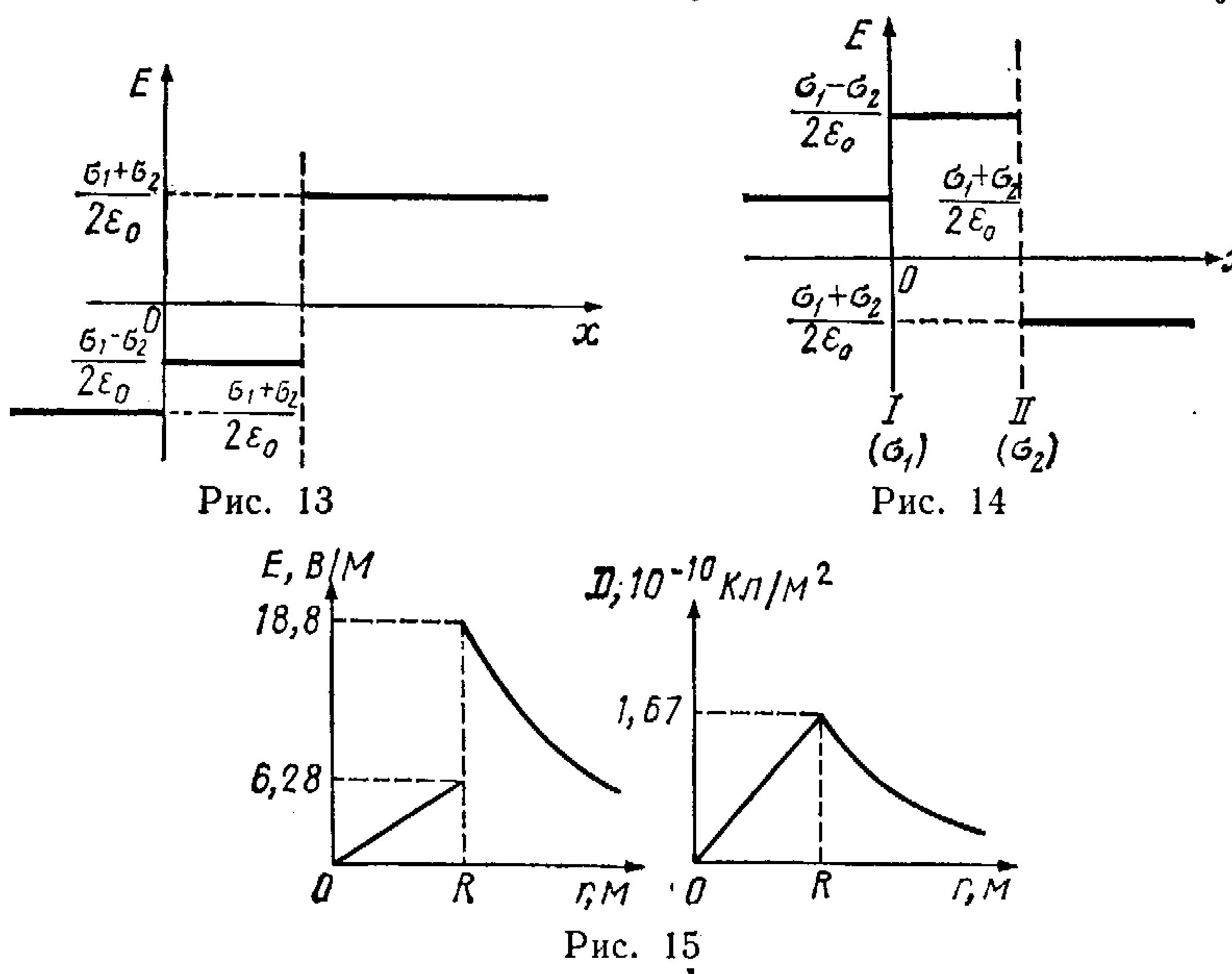 4.16.
E = τ/(8πε0l) = 135
кВ/м. 14.17.
E =
4.16.
E = τ/(8πε0l) = 135
кВ/м. 14.17.
E = ![]() =
55,7 кВ/м.
14.18. 35,6 кВ/м.
14.19.
60,2 кВ/м.
14.20.
38,0 кВ/м.
14.21.
1) E = 0;
2) E =
=
55,7 кВ/м.
14.18. 35,6 кВ/м.
14.19.
60,2 кВ/м.
14.20.
38,0 кВ/м.
14.21.
1) E = 0;
2) E = ![]() =
113 В/м;
график
см. на рис.12.
=
113 В/м;
график
см. на рис.12.
14.22.
1) E1 = ![]() =
113 В/м;2)
E2 =
=
113 В/м;2)
E2 = ![]() = 226 В/м;
график см. на рис.13. 14.23.
1)
396В/.м;
2) 170 В/м;
график
см.
на рис. 14.
14.24.
E =
= 226 В/м;
график см. на рис.13. 14.23.
1)
396В/.м;
2) 170 В/м;
график
см.
на рис. 14.
14.24.
E = ![]() = 377 кB/M.
14.25.
F =
= 377 кB/M.
14.25.
F = ![]() = 16,9 мкН.
14.26.
= 16,9 мкН.
14.26.
![]() = 33,3 нКл.
14.27.
1) Е1 =
= 33,3 нКл.
14.27.
1) Е1 = ![]() =
= 3,78 В/м;
D1 =
=
= 3,78 В/м;
D1 = ![]() = 0,1 нКл/м2;
2) E′2 =
= 0,1 нКл/м2;
2) E′2 = ![]() = 6,28 В/м
(для
r ≤ R);
E″2 =
= 6,28 В/м
(для
r ≤ R);
E″2 = ![]() =
18,8
В/м
(для r ≥ R);
=
18,8
В/м
(для r ≥ R);
 18.8 В/м.
(для r ≥ R);
D'2 = 1/3ρR = 167 пКл/м2;
Eз =
18.8 В/м.
(для r ≥ R);
D'2 = 1/3ρR = 167 пКл/м2;
Eз = ![]() =
4,72 В/м;
D3 =
=
4,72 В/м;
D3 = ![]() =
41,7 пКл/м2;
график см.
на 15.
14.28.
1)
E1 = 0;
D1 = 0;
2)
E2 =
=
41,7 пКл/м2;
график см.
на 15.
14.28.
1)
E1 = 0;
D1 = 0;
2)
E2 =  =13,6
В/м; D2 = 843 пКл/м2;
3) E3 =
=13,6
В/м; D2 = 843 пКл/м2;
3) E3 =  = 229 В/м;
D3 = 2,02 нКл/м2;
график см. на рис. 16.
= 229 В/м;
D3 = 2,02 нКл/м2;
график см. на рис. 16.
14.29.
1) E1 = ![]() = 2,83 В/м;
D1 =
50 пКл/м2;
2) E2 = ρR2/(2ε0r) =
7,55 В/;
D2 = 66,7 пКл/м2,
= 2,83 В/м;
D1 =
50 пКл/м2;
2) E2 = ρR2/(2ε0r) =
7,55 В/;
D2 = 66,7 пКл/м2,
график
см. на рис. 17. 14.30.
E = = ρd/(2ε0ε) =
= 56,5 В/м.
14.31.
ЕА =
= 0;
DA = 0;
ЕB =
= ρd/(4ε0ε) =
80,8 В/м;
DB = ρd/4
= 5 нКл/м2;
E′c = ρd/(2ε0ε) =
162 В/м (х
≤
d);
E″c = ρd/(2ε0) =
= l,13 кВ/м
(x
≤
d);
Dc = ρd/2 = 10 нКл/м2;
график см. на
рис. 18. 14.32.
Действие индуцированного
заряда эквивалентно действию
точечного заряда, являющегося
зеркальным изображением
заряда Q;
F = Q2/(16πε0a2) = 0,9 мкН.
14.33.
E =
![]() = 3,32 кВ/м
(см. задачу 14.32).
14.34.
E = 3Q/(64πε0a2) =
750 В/м.
14.35.
Q =
= 4(аl-sinа)
= 3,32 кВ/м
(см. задачу 14.32).
14.34.
E = 3Q/(64πε0a2) =
750 В/м.
14.35.
Q =
= 4(аl-sinа)![]() =
20 нКл.1
=
20 нКл.1
1 4.36.
F
=
Qτ/(2πε0r)
= 0,36 Η.
14.37.
F
=
Qσ/(2ε0)
=
= 56,5 мкН.
14.38.
σ
=
2ε0F/Q
=
1,06 мкКл/м2.
14.39.
F2
= = ε0F12S/(2Q2)
=
4,92 мН.
14.40.
F/l
=
στ/(2ε0ε)
=
452нН/м. 14.41.
1) 56,5 мН;
2) 0,9 мкН.
14.42.
р = 1/2ε0εE2
= = 27,9 кПа.
14.43.
F/l = τ1τ2/(2πε0r) = 3,6 мН/м.
14.44.
F =
4.36.
F
=
Qτ/(2πε0r)
= 0,36 Η.
14.37.
F
=
Qσ/(2ε0)
=
= 56,5 мкН.
14.38.
σ
=
2ε0F/Q
=
1,06 мкКл/м2.
14.39.
F2
= = ε0F12S/(2Q2)
=
4,92 мН.
14.40.
F/l
=
στ/(2ε0ε)
=
452нН/м. 14.41.
1) 56,5 мН;
2) 0,9 мкН.
14.42.
р = 1/2ε0εE2
= = 27,9 кПа.
14.43.
F/l = τ1τ2/(2πε0r) = 3,6 мН/м.
14.44.
F = ![]() =1,25 мН.
14.45.
F =
=1,25 мН.
14.45.
F = ![]() = 150 мкН.
14.46.
F =
τ1τ2/(πε0) = 36 мН.
14.47.
Ρ = τ1τ2/ε0 = 1,13 мН.
14.48.
F = τ2/(2ε0) = 56,5 мН.
14.49.
ФE = πσr2/(2ε0) = 1,78 кВм.
14.50.
Ψ = 1/2σa2sinβ
= 2,5 нКл.
14.51.
ФE = QS/(4πε0R2)
= 4,5 Вм.
14.52.
Ψ =Qω/(4π)
= 1,19 нКл.
14.53
ФE =
=
= 150 мкН.
14.46.
F =
τ1τ2/(πε0) = 36 мН.
14.47.
Ρ = τ1τ2/ε0 = 1,13 мН.
14.48.
F = τ2/(2ε0) = 56,5 мН.
14.49.
ФE = πσr2/(2ε0) = 1,78 кВм.
14.50.
Ψ = 1/2σa2sinβ
= 2,5 нКл.
14.51.
ФE = QS/(4πε0R2)
= 4,5 Вм.
14.52.
Ψ =Qω/(4π)
= 1,19 нКл.
14.53
ФE =
= ![]() =
2,7 Вм. 14.54.
Ψ=
=
2,7 Вм. 14.54.
Ψ= =
= ![]() = 10 нКл.
= 10 нКл.

14.55.
![]() =
=  = 250 кВ/м. 14.56.
Ψ =
= 250 кВ/м. 14.56.
Ψ =
![]() =
20 нКл.
=
20 нКл.

15.1. 1 кВ. 15.2. A1 = – A = – 4 мкДж; Δφ = A/Q = 200 Β.
15.3.
![]() = – 162 Дж/Кл.
15.4.
A =
= 4,5 мкДж.
Интегрируя в пределах от r1
до
r2
выражение dA = Fdr =
= – 162 Дж/Кл.
15.4.
A =
= 4,5 мкДж.
Интегрируя в пределах от r1
до
r2
выражение dA = Fdr = ![]() ,
найдем
A=
,
найдем
A=![]() ;
потенциальная энергия возрастет на
ΔΠ
=4,5 мкДж.
15.5.
φ
=
45 В.
15.6.
φ=6 кВ,
dmin
= r2-r1
= 10 см;
dmin
= r2+r1 =
40 см.
;
потенциальная энергия возрастет на
ΔΠ
=4,5 мкДж.
15.5.
φ
=
45 В.
15.6.
φ=6 кВ,
dmin
= r2-r1
= 10 см;
dmin
= r2+r1 =
40 см.
15.7.
Ε = Q1/(4πε0) = 664 кВ/м;
φ =
= 664 кВ/м;
φ = ![]() =
26,4 кВ.
15.8.
П =
=
26,4 кВ.
15.8.
П = ![]() = 90 мкДж.
15.9.
П =
=
= 90 мкДж.
15.9.
П =
= ![]() (Q1Q2+Q1Q3+Q2Q3) = – 63 мкДж.
15.10.
Π =
(Q1Q2+Q1Q3+Q2Q3) = – 63 мкДж.
15.10.
Π = ![]() =
48,8 мкДж.
15.11.
П =
=
48,8 мкДж.
15.11.
П =
![]() = 12,7 мкДж,
если заряды одного знака
расположены
в
противоположных
вершинах квадрата; П =
= 12,7 мкДж,
если заряды одного знака
расположены
в
противоположных
вершинах квадрата; П = ![]() = 12,7 мкДж,
если в
противоположных
вершинах заряды разных
знаков.
15.12.
(х–10)2+у2 = 82.
15.13.
ΔΠ
=
= 12,7 мкДж,
если в
противоположных
вершинах заряды разных
знаков.
15.12.
(х–10)2+у2 = 82.
15.13.
ΔΠ
=
= – 498 мкДж.
15.14.
φ = ![]() = 505 В.
15.15.
φ =
= 505 В.
15.15.
φ = ![]() = 62,4 В.
15.16.
φ =
= 62,4 В.
15.16.
φ = ![]() = 36,5 В.
15.17.
33,6 В.
15.18.
Δφ =
= 36,5 В.
15.17.
33,6 В.
15.18.
Δφ = ![]() = 125 В.
15.19.
1)
φ=
= 125 В.
15.19.
1)
φ=
![]() = 360 В;
2) φ =
=
= 360 В;
2) φ =
= ![]() =149 В.
15.20.
1) 75В;
2) 135 В; 3) 100 В.
=149 В.
15.20.
1) 75В;
2) 135 В; 3) 100 В.
15.21.
1) 146 В; 2) 136 В; 3) 100 В; график см.
на рис. 19. 15.22.
1) φ2 = ![]() = 200 B;
2)
φ2 =
= 200 B;
2)
φ2 = ![]() = 100 В.
15.23.
= 100 В.
15.23.
![]() =56,6 В.
15.24.
φ =
= ER = ЗОО кВ;
σ=ε0E
= 55,6 мкКл/м2.
15.25.
U =
=56,6 В.
15.24.
φ =
= ER = ЗОО кВ;
σ=ε0E
= 55,6 мкКл/м2.
15.25.
U = ![]() = 141 В.
15.26.
170 В.
15.27.
1,04.109.
15.28.
432 В.
15.29.
U =
= 141 В.
15.26.
170 В.
15.27.
1,04.109.
15.28.
432 В.
15.29.
U = ![]() =1,2 кВ.
15.30.
ΔΠ =
=1,2 кВ.
15.30.
ΔΠ = ![]() = – 229 эВ.
= – 229 эВ.
1 5.31.
A1,2 =
‑ 1/2Qφ1 = 6 мкДж.
5.31.
A1,2 =
‑ 1/2Qφ1 = 6 мкДж.
15.32.
Δφ = ![]() = 8,07 В.
15.33.
φ1 =
= 8,07 В.
15.33.
φ1 = ![]() = 472 В;
φ, =
= 472 В;
φ, = ![]() =
= 377В;
график см. на рис. 20.
15.34.
1)φ1 =
=
= 377В;
график см. на рис. 20.
15.34.
1)φ1 =  =
238 В; 2)
и 3) φ2 = φ3 = 116 В.
15.35.
gradφ = – E;
|gradφ| = E =
=
238 В; 2)
и 3) φ2 = φ3 = 116 В.
15.35.
gradφ = – E;
|gradφ| = E =
![]() =
226 В/м;
градиент
направлен к плоскости, перпендикулярно
ей. 15.36.
0,6 В.
15.37.
0,12 В. 15.38.
|gradφ|
= φ/r =
= 200 В/м;
градиент направлен к заряду.
15.39.
|gradφ| = τ/(2πε0r) = 180 В/м;
градиент направлен к нити вдоль силовой
линии.
15.40·Δφ =
=
226 В/м;
градиент
направлен к плоскости, перпендикулярно
ей. 15.36.
0,6 В.
15.37.
0,12 В. 15.38.
|gradφ|
= φ/r =
= 200 В/м;
градиент направлен к заряду.
15.39.
|gradφ| = τ/(2πε0r) = 180 В/м;
градиент направлен к нити вдоль силовой
линии.
15.40·Δφ = ![]() =
= 3,14 Β.
15.41
=
= 3,14 Β.
15.41
![]() = 9 мДж.
15.42.
A1,2 =
= 1/3Q1φ1
=1мкДж.
15.43.
= 9 мДж.
15.42.
A1,2 =
= 1/3Q1φ1
=1мкДж.
15.43.
![]() = 659 мкДж.
15.44.
А =
= 659 мкДж.
15.44.
А = ![]() =
= 1,96 мкДж.
15.45.
2,62 мкДж; см. пример 5 на с. 199. 15.46.
А
= Qr/(4ε0)
=
25,2 мкДж.
15.47.·
=
= 1,96 мкДж.
15.45.
2,62 мкДж; см. пример 5 на с. 199. 15.46.
А
= Qr/(4ε0)
=
25,2 мкДж.
15.47.·![]() = 47 мкДж.
15.48.·
= 47 мкДж.
15.48.·![]() = 165 мкДж.
15.49.
A1,2 = l/4Qφ =
250 мкДж.
15.50.
= 165 мкДж.
15.49.
A1,2 = l/4Qφ =
250 мкДж.
15.50.
![]() =
= 62,4 мкДж.
15.51.
S = |е|Et2/(2m) = 1,76 см;
υ =
= |е|Et2/m = 35,2 Мм/с
(m
и е
–
масса
и заряд
электрона).
15.52.
1) 2,55 кВ;
2) 4,69 MB.
15.53.
1,58·1016 м/с2;
5,63 Мм/с;
0,356 нс.
15.54.
15 МэВ;
2,19 м/с.
15.55.
24,3 МКл/кг.
15.56.
l = 3mυ2/(2eE) =
= 5,19 мм.
(m – масса
протона).
15.57.lmin =
l0 – ε0T/(|е|σ) = 1см.
15.58.
2,24 Мм/с;
отклонится
на 45° от первоначального направления.
15.59.
φ2 =
= φΙ ‑
=
= 62,4 мкДж.
15.51.
S = |е|Et2/(2m) = 1,76 см;
υ =
= |е|Et2/m = 35,2 Мм/с
(m
и е
–
масса
и заряд
электрона).
15.52.
1) 2,55 кВ;
2) 4,69 MB.
15.53.
1,58·1016 м/с2;
5,63 Мм/с;
0,356 нс.
15.54.
15 МэВ;
2,19 м/с.
15.55.
24,3 МКл/кг.
15.56.
l = 3mυ2/(2eE) =
= 5,19 мм.
(m – масса
протона).
15.57.lmin =
l0 – ε0T/(|е|σ) = 1см.
15.58.
2,24 Мм/с;
отклонится
на 45° от первоначального направления.
15.59.
φ2 =
= φΙ ‑ ![]() =
289 В
(m
и e – масса
и заряд протона). 15.60.l =
=
289 В
(m
и e – масса
и заряд протона). 15.60.l = ![]() =
2,13 мм.
15.61.
υmin =
=
=
2,13 мм.
15.61.
υmin =
= ![]() = 0,24 Мм/с
(е/т – удельный
заряд электрона.) 15.62.
φ2 = φΙ ‑
= 0,24 Мм/с
(е/т – удельный
заряд электрона.) 15.62.
φ2 = φΙ ‑ ![]() =23,3 В
(т – масса
электрона). 15.63.
Т =
=
=23,3 В
(т – масса
электрона). 15.63.
Т =
= ![]() = 828 эВ.
15.64.
F=2,4·10-17 Η;
a =
= 2,75·1013 м/с2;
υ = 4,07 Мм/c.
15.65.
5,9 мм.
15.66.·79,6 В.
15.67.
22,5 В.
15.68.
rmin =
= 828 эВ.
15.64.
F=2,4·10-17 Η;
a =
= 2,75·1013 м/с2;
υ = 4,07 Мм/c.
15.65.
5,9 мм.
15.66.·79,6 В.
15.67.
22,5 В.
15.68.
rmin =
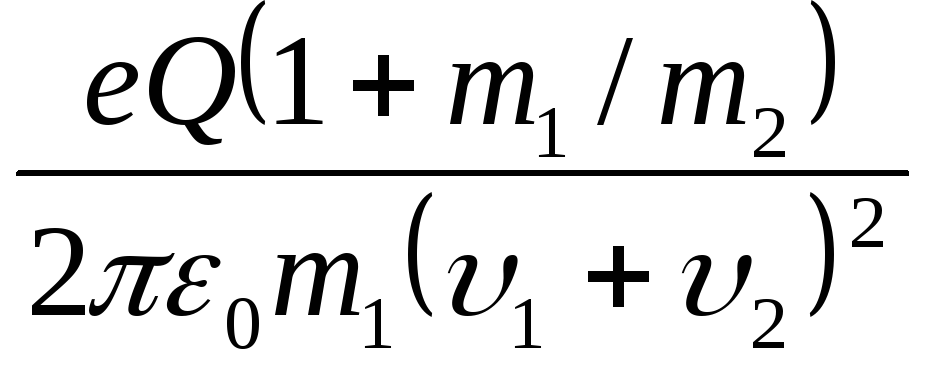 = 7,67 пм
(e – заряд
протона;
Q – заряд
α-частицы);
u1=u2 =m1/(m1+m2)υ = 60 км/с.
15.69.
rmin =
= 7,67 пм
(e – заряд
протона;
Q – заряд
α-частицы);
u1=u2 =m1/(m1+m2)υ = 60 км/с.
15.69.
rmin = ![]() = 72 фм.
15.70.
rmin =
= 72 фм.
15.70.
rmin = ![]() =
10,1 пм
(m – масса
электрона).
15.71.
rmin =
=
=
10,1 пм
(m – масса
электрона).
15.71.
rmin =
=  ;
r01 =
;
r01 = ![]() ;
r01 =
=
;
r01 =
= ![]() .
15.72.
T1 =
.
15.72.
T1 = ![]() ;
1) T1 =
;
1) T1 =
![]() ;
2) T1 =
;
2) T1 = ![]() ;
3) T1 = 0.=
386 В.
;
3) T1 = 0.=
386 В.

16.1.
50 нКлм. 16.2. 6,75 кВ/м.
16.3. EA =
= 1,08 кВ/м; φ0 = 0; EB =
22 кВ/м; φB =
386 B. 16.4.
EA =
9 кВ/м; φA = 0; EB =
18 кВ/м; φB л
= 0,9 В/м; 16.5.
47,6 В/м; 1,8 В. 16.6.
φ =Asinωt, где A =90 В, ω=6,28·103 с-1.
16.7.
<П> = ![]() <sinωt>;
1) <П> =
=
<sinωt>;
1) <П> =
= ![]()
![]() = 14,3 нДж;
2) при
t ≥ T<sinωt>
→ 0 и
<П> = 0.
16.8.
F = 3p1p2/(2πε0r4) =
= 1,35 мкН.
16.9.
П = р1р2/(2πε0r3) =
18 нДж.
16.10.
C = pEsinα/α
= 286 нНм/рад.
16.11.
С = pE =
= 300 нНм/рад.
16.12.
П = – pEcosα
= – 500 мкДж.
16.13.
A = 2рE
= 30 мкДж.
16.14.
ΔΠ == рЕ(1 – cosα) = 0,5мкДж.
16.15.
ω =
= 14,3 нДж;
2) при
t ≥ T<sinωt>
→ 0 и
<П> = 0.
16.8.
F = 3p1p2/(2πε0r4) =
= 1,35 мкН.
16.9.
П = р1р2/(2πε0r3) =
18 нДж.
16.10.
C = pEsinα/α
= 286 нНм/рад.
16.11.
С = pE =
= 300 нНм/рад.
16.12.
П = – pEcosα
= – 500 мкДж.
16.13.
A = 2рE
= 30 мкДж.
16.14.
ΔΠ == рЕ(1 – cosα) = 0,5мкДж.
16.15.
ω = ![]() = 6 рад/с.
16.16.
ν =
= 6 рад/с.
16.16.
ν = ![]() =239 Гц.
16.17.
F = pdE/dx = 0,2 мН.
=239 Гц.
16.17.
F = pdE/dx = 0,2 мН.
16.18.
![]() = 1,8 МВ/м2;
F =
= 1,8 МВ/м2;
F = ![]() = 9 мкН.
16.19.
= 9 мкН.
16.19.
![]() =
= 0,9 МВ/м2;
F =p
=
= 0,9 МВ/м2;
F =p![]() = 3,9 мкН.
16.20.
1) e;
2) e;
3) е;
4) е,
а,
о; 5) е,
а,
о;
6)
е, а,
о;
7)
е, а;
8)
е, а, о,
е; 9)
е,
а,
16.21.
0,695·10-19 Кл;
электронное облако вблизи протона лишь
частично смещается к ядру
атома
фтора.
16.22.
6; 47,7 мкКл/м2.
16.23.
σ΄1 =
=
= 3,9 мкН.
16.20.
1) e;
2) e;
3) е;
4) е,
а,
о; 5) е,
а,
о;
6)
е, а,
о;
7)
е, а;
8)
е, а, о,
е; 9)
е,
а,
16.21.
0,695·10-19 Кл;
электронное облако вблизи протона лишь
частично смещается к ядру
атома
фтора.
16.22.
6; 47,7 мкКл/м2.
16.23.
σ΄1 =
= ![]() = 0,255 мкКл/м2;
σ΄2 =
= 0,255 мкКл/м2;
σ΄2 = ![]() = 0,130 мкКл/м2.
16.24. ± 11,8 мкКл/м2.
16.25.
77,4 МВ/м. 16.26.
555 кВ/м. 16.27.
В 1,5 раза. 16.28.
1,015. 16.29.
1) 0,1%; 2) 25%. 16.30.
Р =
= 0,130 мкКл/м2.
16.24. ± 11,8 мкКл/м2.
16.25.
77,4 МВ/м. 16.26.
555 кВ/м. 16.27.
В 1,5 раза. 16.28.
1,015. 16.29.
1) 0,1%; 2) 25%. 16.30.
Р = ![]() =
152 мкКл/м2.
16.31.
11,3 МВ/м. 16.32.
Ρ =
= (ε – 1)ε0E0/ε = 37,9 мкКл/м2.
16.33.
142 кНл/м2.
16.34.
1) 1,44;
2)
6,3·10-4 Клм.
16.35.
0,03. 16.36. αn ≤ 0,183.
16.37.
α = 3M(ε – 1)/[ρΝΑ
(ε + 2)] =
= 2,24·10-29м3.
16.38.
1) χ = αn = 2,7.10-4.
2)
χ. =
3ρNAα/(3M – ρNAα) = 0,23.
16.39.
ε =
=
152 мкКл/м2.
16.31.
11,3 МВ/м. 16.32.
Ρ =
= (ε – 1)ε0E0/ε = 37,9 мкКл/м2.
16.33.
142 кНл/м2.
16.34.
1) 1,44;
2)
6,3·10-4 Клм.
16.35.
0,03. 16.36. αn ≤ 0,183.
16.37.
α = 3M(ε – 1)/[ρΝΑ
(ε + 2)] =
= 2,24·10-29м3.
16.38.
1) χ = αn = 2,7.10-4.
2)
χ. =
3ρNAα/(3M – ρNAα) = 0,23.
16.39.
ε =
= (3Μ – 2χρVom)/(3M – χρVom); ε1 = 1,51; ε2 = 1,61. 16.40. 1,13см3. 16.41. 1,87·10-30 м3; ε = 1+αn= = 1,00005. 16.42. 1,65·10-36 Клм; 1,03·10-17м. 16.43. 2,0·10-29м3. 16.44. 5,1·10-31 Клм. 16.45. 4·10-33 Клм. 16.46. 11,7 мДж/м3. 16.47. 1,04·10-29 м3.
16.48.
2,02·10-29 м3.
16.49.
ε =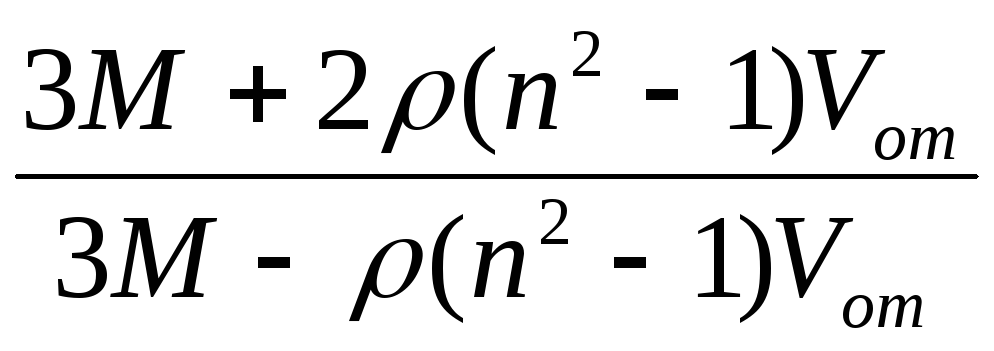 =
= 2,02·
16.50.
2,14.
·
16.51.
αe = ЗМ(n2 –1)/[ρNА(n2+2)]
=
1,05·10-28 м3.
16.52.
ε =
(1+2β)/(1 – β) = 1,52,
где β = αρNA/(3M);
n =
=
= 2,02·
16.50.
2,14.
·
16.51.
αe = ЗМ(n2 –1)/[ρNА(n2+2)]
=
1,05·10-28 м3.
16.52.
ε =
(1+2β)/(1 – β) = 1,52,
где β = αρNA/(3M);
n = ![]() = 1,23.
16.53.
n =
= 1,23.
16.53.
n = ![]() =1,20,
где
=1,20,
где
 .
16.54. 3,38·10-28 м3.
16.55.
0,046.
16.56.
326 К.
16.57.
В 1,27
раза.
.
16.54. 3,38·10-28 м3.
16.55.
0,046.
16.56.
326 К.
16.57.
В 1,27
раза.

17.1.
1,11 пΦ.
17.2.
180 пΦ.
17.3.
712 мкФ.
17.4.
σ1 =
49,8 нКл/м2;
σ2 =
16,6 нКл/м2.
17.5.
φ =
(R1φ1 + R2φ2)/(R1 + R2) =
380 В·
17.6.
6,2 нФ.
17.7.
1) 88,5 пΦ;
2)
D1 = D2 = 2,66 мкКл/м;
Ег =
42,8 кВ/м;
E2 =
100 кВ/м;
Δφ1 = Δφ2 =300 В.
17.8.
C =
ε0S  = 35.4 пΦ.(ε3 диэлектрическая
проницаемость воздуха). 17.9. ΔU =
(σ/ε0)(d2 – d1) =
= 22,6 В.
17.10.
0,5 см.
17.11.
2,5 мкФ.
17.12.
700 В.
17.13.
С = 4πεε0R1R2/(R2 – R1) =
93,3 пФ.
17.14.
4,41 кВ.
17.15.
5.
17.16.
1) 360 мкКл,
720 мкКл,
120 В;
2)
240 мкКл, 80 В, 40 В. 17.17.
C2
=
=
= 35.4 пΦ.(ε3 диэлектрическая
проницаемость воздуха). 17.9. ΔU =
(σ/ε0)(d2 – d1) =
= 22,6 В.
17.10.
0,5 см.
17.11.
2,5 мкФ.
17.12.
700 В.
17.13.
С = 4πεε0R1R2/(R2 – R1) =
93,3 пФ.
17.14.
4,41 кВ.
17.15.
5.
17.16.
1) 360 мкКл,
720 мкКл,
120 В;
2)
240 мкКл, 80 В, 40 В. 17.17.
C2
=
= ![]() = 0,32 мкФ.
17.18. ΔQ =
= 0,32 мкФ.
17.18. ΔQ =
![]() =
36 мкКл.
17.19.
2,32 мм. 17.20.
С = (С1 + С2)(С3 + С4)/(C1 + C2 + C3 + C4) =
0,21 мкФ.
17.21.
U1 = С2U/(С1 + С2) =
240 В;
U2 = C1U/(C1 + C2)
=80 B;
U3 = C4U/(C3 + C4)=120 B;
U4=С3U/(С3 + С4) =
200 В;
Q1
= Q2
= C1C2U/(C1 + C2)
=
48 мкКл;
Q3
= Q4 =
= С3С4U/(С3 + С4)
=
60 мкКл.
17.22. С=
=
36 мкКл.
17.19.
2,32 мм. 17.20.
С = (С1 + С2)(С3 + С4)/(C1 + C2 + C3 + C4) =
0,21 мкФ.
17.21.
U1 = С2U/(С1 + С2) =
240 В;
U2 = C1U/(C1 + C2)
=80 B;
U3 = C4U/(C3 + C4)=120 B;
U4=С3U/(С3 + С4) =
200 В;
Q1
= Q2
= C1C2U/(C1 + C2)
=
48 мкКл;
Q3
= Q4 =
= С3С4U/(С3 + С4)
=
60 мкКл.
17.22. С=
![]() = 20 пкФ.
17.23.
200 мкКл;
120 мкКл;
120 мкКл;
100 мкКл;
110 В;
60 В;
40 В;
220 мкКл;
210 В.
17.24.
2 пФ.
Указание.
Доказать,
что если C1/C2 = C3/C4,
то
φA = φB
и, следовательно, емкость С5
при
определении
общей емкости схемы значения не имеет.
17.25.
С4 =
= С2С3/С1=9 пкФ.
= 20 пкФ.
17.23.
200 мкКл;
120 мкКл;
120 мкКл;
100 мкКл;
110 В;
60 В;
40 В;
220 мкКл;
210 В.
17.24.
2 пФ.
Указание.
Доказать,
что если C1/C2 = C3/C4,
то
φA = φB
и, следовательно, емкость С5
при
определении
общей емкости схемы значения не имеет.
17.25.
С4 =
= С2С3/С1=9 пкФ.
1 8.1.
0,05 мкДж.
18.2.
30 мкДж;
15 мН.
18.3.
0,209 Дж.
18.4.
2,5 Дж/м3.
18.5.
50 мкДж.
18.6.
1500 В;
0,2 мДж.
18.7.
0,3 мДж.
18.8.
1) 0,18 Дж,
0,09 Дж,
0,06 Дж;
2)
0,605 Дж,
1,21 Дж, 1,82 Дж.
18.9.
80 мкДж.
18.10.
А =
8.1.
0,05 мкДж.
18.2.
30 мкДж;
15 мН.
18.3.
0,209 Дж.
18.4.
2,5 Дж/м3.
18.5.
50 мкДж.
18.6.
1500 В;
0,2 мДж.
18.7.
0,3 мДж.
18.8.
1) 0,18 Дж,
0,09 Дж,
0,06 Дж;
2)
0,605 Дж,
1,21 Дж, 1,82 Дж.
18.9.
80 мкДж.
18.10.
А = ![]() =
= 63,5 нДж
(ε – диэлектрическая
проницаемость
фарфора). 18.11.
1) σ = ε0E(ε – 1)/ε = 5,9 нКл/м2
(ε –
диэлектрическая
проницаемость
эбонита);
2)
W =
= 1/2ε0
(E2/ε)Sd
= 88,5 пДж.
18.12.
W =
=
=
= 63,5 нДж
(ε – диэлектрическая
проницаемость
фарфора). 18.11.
1) σ = ε0E(ε – 1)/ε = 5,9 нКл/м2
(ε –
диэлектрическая
проницаемость
эбонита);
2)
W =
= 1/2ε0
(E2/ε)Sd
= 88,5 пДж.
18.12.
W =
= ![]() Sd = 118 пДж.
18.13.
0,55 мкДж.
18.14.
450 мкДж. 18.15.
30 мкДж.
18.16.
W =
Q/(l6πεε0R) =
225 мкДж.
18.17.
12см.
18.18.
W1=
Sd = 118 пДж.
18.13.
0,55 мкДж.
18.14.
450 мкДж. 18.15.
30 мкДж.
18.16.
W =
Q/(l6πεε0R) =
225 мкДж.
18.17.
12см.
18.18.
W1= ![]() = 7,88 нДж;
W2 =
= 7,88 нДж;
W2 = ![]() =
78,8 пДж.
18.19.
W1/W2 = 5ε = 15
(ε – диэлектрическая
проницаемость среды, в которой находится
шар; см. задачу 18.18).
=
78,8 пДж.
18.19.
W1/W2 = 5ε = 15
(ε – диэлектрическая
проницаемость среды, в которой находится
шар; см. задачу 18.18).
1 9.1.
15 Кл. 19.2.
6,1 МА/м2.
19.3.
34,2 мм2.
19.4.
2,58 мОм.
19.5.
18,80 м.
19.6.
5/6 Ом.
19.7.
3/4 Ом.
19.8. 7/12 Ом.
19.9.
250 Ом;
20%.
19.10.
2 А.
19.11.
Для схемы а) 16,7%; 0,2%.
Для
схемы б) 0,2%;
20%.
19.12.
1,48%.
19.13.
2,9 Ом;
4,5 Ом.
19.14.
2 А.
19.15.
n =
9.1.
15 Кл. 19.2.
6,1 МА/м2.
19.3.
34,2 мм2.
19.4.
2,58 мОм.
19.5.
18,80 м.
19.6.
5/6 Ом.
19.7.
3/4 Ом.
19.8. 7/12 Ом.
19.9.
250 Ом;
20%.
19.10.
2 А.
19.11.
Для схемы а) 16,7%; 0,2%.
Для
схемы б) 0,2%;
20%.
19.12.
1,48%.
19.13.
2,9 Ом;
4,5 Ом.
19.14.
2 А.
19.15.
n =![]() ;
Ri = R
19.16.
Четыре параллельно
соединенных группы по три последовательно
соединенных элемента в
каждой; 7,5 А.
19.17.
а) I =
3 Α,
U = 0;
б)
I = 0,
U = 1,2 В.
19.18.
0,5 А.
19.19.
1,6 А;
0,2 А; 1,4 А. 19.20.
0. 19.21.
I3 =
0; U3 =
0.
19.22.
3 А;
4 А;
1 А.
19.23.
0,8 А;
0,3 А;
0,5 А.
19.24.
3,6 В. 19.25.
2 А. 19.26.
15 Вт. 19.27.
0,5 Ом; 2 Вт. 19.28.
0,4; 297 Ом. 19.29.
I1 = 20 А,
η1 =
0,17; I2 =
4 А,
η2 =
0,83.
19.30.
45 мин, 10 мнн. 19.31.
12 В; 20 Ом. 19.32.
Q =
=
;
Ri = R
19.16.
Четыре параллельно
соединенных группы по три последовательно
соединенных элемента в
каждой; 7,5 А.
19.17.
а) I =
3 Α,
U = 0;
б)
I = 0,
U = 1,2 В.
19.18.
0,5 А.
19.19.
1,6 А;
0,2 А; 1,4 А. 19.20.
0. 19.21.
I3 =
0; U3 =
0.
19.22.
3 А;
4 А;
1 А.
19.23.
0,8 А;
0,3 А;
0,5 А.
19.24.
3,6 В. 19.25.
2 А. 19.26.
15 Вт. 19.27.
0,5 Ом; 2 Вт. 19.28.
0,4; 297 Ом. 19.29.
I1 = 20 А,
η1 =
0,17; I2 =
4 А,
η2 =
0,83.
19.30.
45 мин, 10 мнн. 19.31.
12 В; 20 Ом. 19.32.
Q =
= ![]() =100 кДж.
19.33.
1 кДж (см. задачу 19.32.).
19.34.
q = 1/2
=100 кДж.
19.33.
1 кДж (см. задачу 19.32.).
19.34.
q = 1/2![]() = 20 Кл.
Решение.
Из условия равномерности возрастания
тока следует I
= kt, или
dq/dt
= kt, где
k—коэффициент
пропорциональности,
отсюда
dq = ktdt
и
q = k
= 20 Кл.
Решение.
Из условия равномерности возрастания
тока следует I
= kt, или
dq/dt
= kt, где
k—коэффициент
пропорциональности,
отсюда
dq = ktdt
и
q = k![]() .
Значение
k
найдем
из выражения количества
теплоты, выделившегося и проводнике:
dQ = I2rdt = k2rt2dt.
Интегрируя,
получим Q = k
.
Значение
k
найдем
из выражения количества
теплоты, выделившегося и проводнике:
dQ = I2rdt = k2rt2dt.
Интегрируя,
получим Q = k![]() .
Отсюда
k =
= 1/2
.
Отсюда
k =
= 1/2![]() После
подстановки
получим q = 1/2
После
подстановки
получим q = 1/2![]() =
20 Кл.
19.35.
<I> = 1/2
=
20 Кл.
19.35.
<I> = 1/2![]() =
= 10 А
(см.
задачу 19.34).
19.36.
=
= 10 А
(см.
задачу 19.34).
19.36.
![]() =l А/с
(см. задачу 19.34.)·
=l А/с
(см. задачу 19.34.)·
