Математическая логика и теория алгоритмов

Лекция 1

1. Логика высказываний

2. Логика предикатов

3. Метод резолюций в логике высказываний

4. Метод резолюций в логике предикатов

5. Теория алгоритмов

Формальная логика — конструирование и исследование правил преобразования высказываний, сохраняющих их истинностное значение безотносительно к содержанию входящих в эти высказывания понятий. Автором первой системы формальной логики считается Аристотель, живший в IV веке до нашей эры. Математическая логика зародилась в конце XIX века, а основное развитие происходило в первой половине XX века.

В XIX веке немецкий ученый Кантор создает теорию множеств, которая быстро становиться очень популярной и ей присваивается значение «корень всей математики».

Но в конце XIX веке были открыты логические парадоксы, которые доказали, что теория множеств не является основной (методы, построенные на этой теории могут быть ошибочны). Логические парадоксы – третий кризис в математике. Парадокс – рассуждение, приводящее к противоречию. Сущность парадокса заключается в том, что с помощью логически правильных рассуждений удается обосновать (доказать средствами данной теории) одновременно некоторое утверждение и его отрицание, т.е. противоречие. После их обнаружения появилась немедленная потребность в новом обосновании математики, то есть построить такую математику, чтобы в ней не было парадоксов. Для этого нужно было найти причину парадоксов.

Математическая логика – наука, позволяющая выявить правильные подходы.

К примеру, рассмотрим парадокс лжеца.

Допустим, некто говорит: «Я лгу». Рассмотрим эту ситуацию с двух позиций. Если это некто лжет, тогда фраза «Я лгу» - ложь. Значит, некто говорит правду. С другой стороны, если некто не лжет – «Я лгу» означает ложь. Следовательно, некто лжет.

лжет → не лжет

не лжет → лжет

Мы пришли к противоречию.

Рассмотрим другой пример – парадокс брадобрея.

На острове Крит жил один брадобрей, который бреет всех, кто не бреет себя сам. Кто бреет брадобрея?

Если провести такую же логическую работу, рассмотреть две ситуации, как и в предыдущем примере, то получиться такая схема:

бреет себя сам → не бреет себя

не бреет себя → бреет себя сам

Мы опять пришли к противоречию.

В 1902 году Бертраном Расселом был открыт Парадокс Рассела, один из парадоксов теории множеств Кантора.

Существуют множества, состоящие из элементов. Есть множества, элементами которых являются множества. Некоторые множества не являются элементами самих себя. Также существуют множества, которые являются элементами самих себя.

Пусть М – множество всех множеств, М М.

С – множество всех множеств, которые не принадлежат себе в качестве элементов.

С={X: }

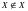С (С является элементом самого себя) →

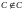
(С не является элементом самого себя) →

Благодаря кризису стали развиваться новые науки. Математическая логика является одним из новых направлений для преодоления кризиса.

Составляющие науки:

1. Предмет изучения (объект)

2. Язык описания

Например, изучать английский язык мы будем с помощью русского языка. В данном случае, английский язык – язык объект, а русский язык – язык описания, метаязык.

В парадоксе лжеца к предложению метаязыка «Я лгу» мы относились как к предложению объектного языка. Парадокс лжеца заключается в том, что элемент одного множества был перенесен в другое множество. Парадокс брадобрея заключается в том же.

Множества всех множеств не существует.

Лекция 2

Логика высказываний.

Одной из основных задач логики является формализация или символизация естественного языка. Это позволит исключить неясности, двусмысленности, присущие естественному языку. Так как мышление выражается в речи - это позволяет структурировать законы мышления и точно их описать.

Логика высказывания – простейшая логическая теория. В ней считается, что наша речь состоит из высказываний.

Высказыванием называется повествовательное предложение, утверждение, которое либо ложно, либо истинно. Примеры высказываний: «Москва – столица России» - истинное высказывание (И), «Волга впадает в Черное море» - ложное высказывание (Л), «Существуют внеземные цивилизации» - высказывание, значение которого неизвестно. «Площадь комнаты равна 25 м²» - не является высказыванием, потому что нельзя приписать значение ложь или истина, нет определенности (может быть любая комната).

Логика высказываний объединяет нашу речь. В логике высказываний нельзя охватить всю нашу речь.

«Если завтра будет хорошая погода, то я пойду в театр или не пойду в кино» - сложное высказывание, состоит из простых высказываний «Завтра будет хорошая погода», «Я пойду в театр», «Я пойду в кино». С помощью союзов «Если…, то», «или» и частицы «не» мы из простых высказываний получили сложное высказывание. Союзы и частица «не» превращают одни высказывания в другие, следовательно, они являются операциями над высказываниями.

В логике высказываний используются только эти союзы: «и», «или», «если…,то», «тогда и только тогда, когда» и частица «не».

Заглавные латинские буквы А, В… обозначают конкретные высказывания.

А=И – высказывание истинно.

А=Л – высказывание ложно.

Если не учитывать смысл предложения, а учитывать только их значение – истина или ложь – то можно сказать, что А, В являются переменными, которые применяют значения из бинарного множества - {Л, И} – множество истинностных значений.

А, В принадлежат множеству{Л,И}.

Введем математические операции, которые моделируют содержательные союзы и частицу «не».

1. Отрицание (¬) – одноместная (унарная) операция, результат которой записывается так «¬А» и означает «не А» и «не верно, что А». Отрицание всегда ставиться в начале предложений. Таблица истинности отрицания:

А	¬А
Л	И
И	Л

2. Конъюнкция (&) двухместная (бинарная) операция. Конъюнкция называется логическим умножением. Результат записывается так «А&В» и означает «А и В», «А конъюнкция В», «А умножить на В».

Таблица для конъюнкции:

А	В	А&В
Л	Л	Л
Л	И	Л
И	Л	Л
И	И	И

3. Дизъюнкция (v) двуместная (бинарная) операция. Дизъюнкция называется логическим сложением. Результат записывается так «АvВ» и означает «А или В», «А дизъюнкция В», «А плюс В».

Таблица для дизъюнкции:

А	В	АvВ
Л	Л	Л
Л	И	И
И	Л	И
И	И	И

«v» - соответствует союзу «или» в соединительном смысле, что видно из последней строки таблицы.

Строгая дизъюнкция соответствует союзу «или» в разделительном смысле – «А либо В». Таблица такая же, что и дизъюнкции.

4. Импликация (→) – двуместная (бинарная) операция. Импликация называется логическим следованием. Результат записывается так «А→В» и означает «если А, то В», «из А следует В», «А влечет В», «А достаточно для В», «В необходимо для А», «В тогда, когда А», «А только тогда, когда В».

Таблица для импликации:

А	В	А→В
Л	Л	И
Л	И	И
И	Л	Л
И	И	И

Первые две строки не соответствуют тому, что мы говорим. Например, «Если 2×2=5, то Москва столица России». Первая часть выражения ложна, а вторая истинна. В нашей логике высказываний это будет допустимое истинное выражение.

А&В→А – эта импликация должна быть истинной в любом случае.

Импликация не вполне соответствует союзу «если, то». Несоответствие получается из-за того, что мы учитываем значение, но никак не содержание. «Из лжи следует все, что угодно».

5. Эквивалентность (≡) или (↔) – двуместная (бинарная) операция. Результат записывается так «А≡В» и означает «А эквивалентно В», «А тогда и только тогда, когда В», «А необходимо и достаточно для В».

Таблица для эквивалентности:

А	В	А≡В
Л	Л	И
Л	И	Л
И	Л	Л
И	И	И

Всего пять операций – отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность (¬,& , v, →, ≡).

Множество истинностных значений {Л,И} с введенными операциями (¬,& , v) называется алгеброй логики.

{Л,И} – носитель алгебры логики, (¬,& , v) – сигнатура.

Формулы логики высказываний (алгебры логики).

Формулой называется конечная последовательность символов некоторого алфавита, построенная по определенному правилу.

Алфавит логики высказываний:

1. Печатные заглавные латинские буквы А,В…, с индексами или без – пропозициональные буквы (франц. Propose – слово, предложение).

2. ¬,& , v, →, ≡ - пропозициональные связки

3. Круглые скобки () – вспомогательные символы.

Любая последовательность символов алфавита называется выражением логики высказываний. Формулы – это так называемые правильные выражения. Они также называются пропозициональными формами (высказывательные формулы).

Определение.

1. Все пропозициональные буквы являются формулами. А, В,… - формулы.

2. Если А,В …(не путать с А,В) – формы, то формами являются также и выражения (¬А), (А&В), (АvВ), (А→В), (А≡В).А,В – подформы.

3. Других форм нет.

Это определение, состоящее из трех пунктов – индуктивное определение.

Также существуют дедуктивные определения. При дедуктивном определении для определения нового понятия мы обращаемся к более полному (общему) понятию и дополнительно ограничиваем его.

Дедукция – от общего к частному.

Индукция – от частного к общему.

Лекция 3.

Правила сокращенной записи форм:

1. Стандартный порядок выполнения операций: ¬,& , v, →, ≡.

2. Операция отрицания действует на минимальную форму, стоящую справа.

3. & , v, →, ≡ данные операции действуют на минимальные формы слева и справа.

4. Вхождение одной и той же связки выполняется слева направо.

5. Внешние скобки отбрасываются.

Интерпретация форм.

Интерпретировать формальный объект значит приписать ему некоторый смысл.

А = А (А₁,…А_n).

I интерпретация:

1) Буквы интерпретируем как истинностные переменные. А₁,…А_n принадлежит {Л,И}.

2) Связки ¬,& , v, →, ≡ интерпретируются как символы логических операций с известными нам таблицами.

3) Скобки () никак не интерпретируются.

Таким образом, задав значения букв можно по таблицам операций вычислить значение формы, которое тоже будет истинностным.

Таким образом, мы видим, что форма порождает истинностную функцию.

f _А:{Л,И}ⁿ→{Л,И}

Таблица этой функции содержит 2 ⁿ строк.

Наборы записываются в таблицу лексикографическом порядке, считая, что Л<И.

II интерпретация (можно использовать для интерпретированного языка).

1)Буквы А₁,…А_n - понимаются как простейшие высказывания, значения которых известны.

2) Связки ¬,& , v, →, ≡ интерпретируются как союзы и частица «не».

3) Скобки () никак не интерпретируются.

Тогда форма А превращается в сложное высказывание.

Тавтологии и противоречия. Логически истинные высказывания.

Дана произвольная форма А = А (А₁,…А_n).

Высказывание, полученное из формы А подстановкой вместо букв конкретных простых высказываний называется частным случаем формы. У одной формы может быть бесконечное число частных случаев формы.

Форма А называется выполнимой, если существует набор значений букв не которых А равно истине (А =И) (у формы существует истинный частный случай).

Форма А называется тавтологией, если она истинна при любых значениях букв, то есть порождает тождественно истинную функцию (а таблице одни истины).

Форма А называется противоречием, если ложна при всех значениях букв, то есть порождает тождественно ложную функцию (в таблице одна ложь).

Высказывание называется логически истинным, если оно является частным случаем тавтологии или логическим ложным, если оно является частным случаем противоречия.

Истинное высказывание.

Логически истинное высказывание истинно в силу своей структуры, а не содержания.

А =Аv¬А – тавтология

Пример:

А =(2×2=5) или (2×2≠5) = И – логически истинное высказывание

То же самое относится и к логически ложным высказываниям.

А ~Т – означает, что форма является тавтологией.

А ~П означает, что форма является противоречием.

Проблема выполнимости логики высказываний.

Пусть дана произвольная форма А = А (А₁,…А_n).

Проблема: существует ли метод, позволяющий за конечное число шагов или действий выяснить выполнимость произвольно заданной формы?

А может быть выполнимой, не выполнимой (А ~П), тавтологией (А ~Т, частный случай выполнимой формы).

А ~П ↔ ¬ А ~Т – форма А является противоречием тогда и только тогда, когда ¬ А является тавтологией.

Такой метод существует и он называется методом построения таблиц.

Количество строк определяется формулой 2ⁿ, где n кол-во переменных.

Если форма содержит К связок, то нужно выполнить К операций.

Чтобы вычислить форму необходимо К×2ⁿ < ∞ (число конечное).

Этот метод не совсем удобен.

Существует другой метод, основанный на построении других форм Д.Н.Ф. и К.Н.Ф.