9. Основные понятия и величины динамики поступательного движения

Основные формулы 

1. Уравнение динамики поступательного движения тела:

, где m – масса тела,   – его ускорение,   – сумма всех действующих на тело сил.

2. Импульсом тела называется произведение массы тела  на его скорость:                                          .

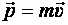3. Закон изменения импульса: 

 =  .

4. Работой силы F на перемещении ds называется произведение проекции силы на направление перемещения на это перемещение:

dA = F_s ds = Fds cosα, где α – угол между направлениями силы и перемещения.

5. Работа переменной силы вычисляется как:

A =  .

6. Мощностью называют работу, произведенную за единицу времени:                                           N =  .

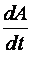7. Мгновенная мощность равна скалярному произведению силы, действующей на тело, на его скорость:

N =  .

8. Кинетическая энергия тела при поступательном движении:

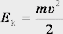, где  m – масса тела, υ – его скорость.

9. Потенциальная энергия тела

– в однородном поле тяжести: 

E_п  =  mgh (m – масса тела, g – ускорение свободного падения, h – высота тела над точкой, в которой потенциальная энергия принимается равной нулю);

– в поле упругих сил:

E_п =  (k – коэффициент жесткости упругого тела, x – смещение от положения равновесия).

10. В замкнутой системе частиц полный импульс  системы не меняется в процессе ее движения:

Σ   = const.

11. В замкнутой консервативной системе частиц сохраняется полная механическая энергия:

E = E_k + E_п = const.

12. Работа сил сопротивления равна убыли полной энергии системы частиц или тела:                         A_conp = E₁ – E₂.

9. Импульс релятивистской частицы:

1. Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

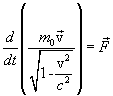, где  - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы,  - сила действующая на частицу. Сопоставим с классическим уравнением

Мы приходим к выводу, что релятивистский импульс частицы равен

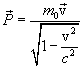
2. Релятивистская масса.

Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.

3. Энергия в релятивистской динамике.

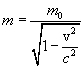
Для энергии частицы в теории относительности получается выражение:

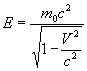
Покоящаяся частица обладает энергией

Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

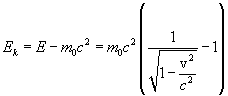
Приняв во внимание, что  , выражение для полной энергии частицы можно написать в виде

Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела   сопровождается изменением массы тела и, наоборот, всякое изменение массы   сопровождается изменениемэнергии  . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.