4. Концентрация напряжений

Введение

Разрушение деталей машин и сооружений практически всегда на­чинается в местах локальной концентрации напряжений, обуслов­ленной геометрическими или микроструктурными разрывами. В этих местах, называемых концентраторами напряжений, локаль­ные напряжения часто во много раз превосходят номинальные, т. е. определенные без учета эффектов концентрации. Качественно разобраться в концентрации напряжений, связанной с геометриче­скими особенностями, можно, рассмотрев «течение сил» в элементе под действием нагрузок. Иллюстрация такого пояснения дана на рис. 23.

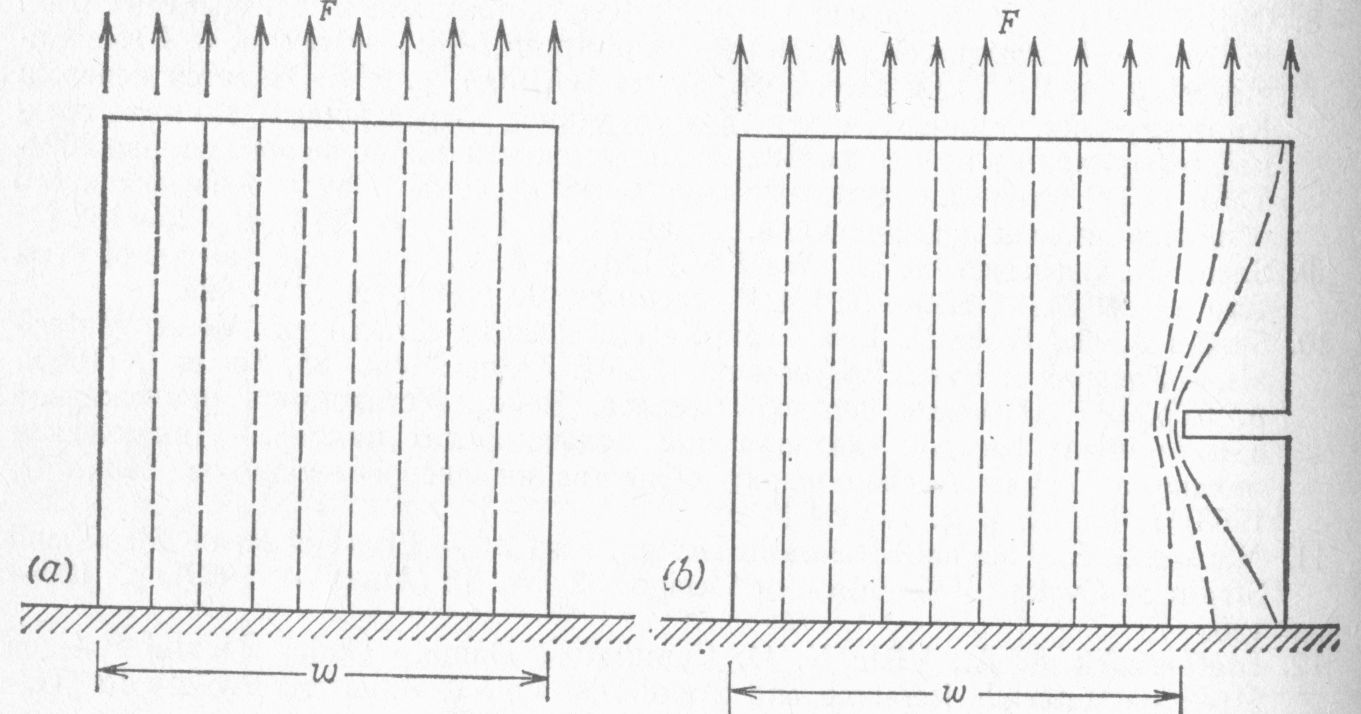
Рис. 23. Интуитивное представление о концентрации напряжений, (а) без кон­центрации напряжений; (b) при наличии концентрации напряжений

На рис. 23(a) изображена прямоугольная пластина шириной w и толщиной t, заделанная на нижнем краю и нагруженная равно­мерно распределенными усилиями с равнодействующей F по верх­нему краю. Каждая из штриховых линий означает некоторую часть силы, а локальное расстояние между линиями соответствует ло­кальной плотности усилий, т. е. напряжению. На рис. 23(a) линии распределены равномерно по области, занятой пластиной, напряжения распределены тоже равномерно, и вычислить их можно по стандартной формуле.

На рис. 23(b) показана прямоугольная пластина, нагружен­ная такой же равнодействующей силой, но эта пластина шире и у нее имеется такой вырез, что ширина ее в районе выреза тоже равна w. На рис. 23(b) ясно видно, что через вырез силы не могут передаваться, поэтому силовые линии должны огибать вершину выреза. При этом силовые линии у вершины выреза локально сгу­щаются, что свидетельствует об увеличении интенсивности усилий или напряжений в вершине выреза. Таким образом, около вершины выреза имеет место локальное увеличение, или концентрация, на­пряжений. Хотя номинальное напряжение по сечению пластины в районе выреза все еще вычисляется по стандартной формуле, в действи­тельности локальное напряжение в вершине выреза может во много раз превосходить номинальное напряжение.

Можно привести множество примеров концентрации напряже­ний; некоторые из них показаны на рис. 24. Основания зубьев шестерен, угловые точки шпоночных канавок в валах, впадины вин­товых резьб, скругления уступов валов, отверстия под заклепки и болты и окрестности сварных швов являются концентраторами напряжений, которые, как правило, должны исследоваться кон­структором. Степень опасности концентрации напряжений зависит от вида нагружения, типа материала, размера и формы геометри­ческой особенности.

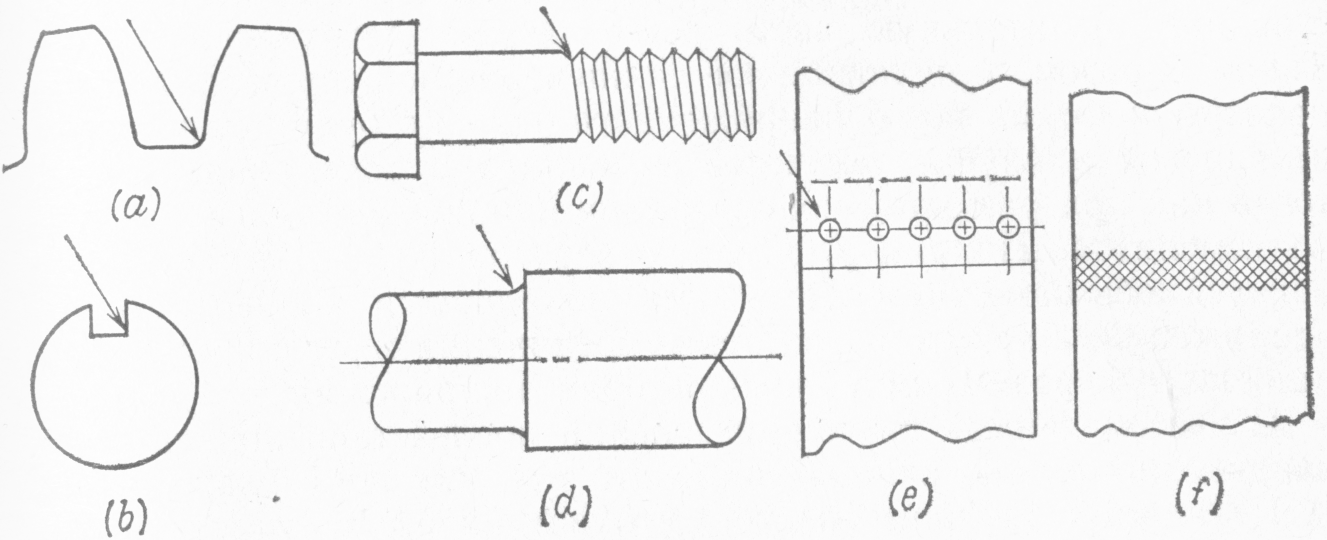
Рис. 24 Примеры концентрации напряжений в деталях

2. Последствия

С целью изучения последствий концентрации напряжений концент­раторы напряжений можно разделить на локальные и раз­мытые. Весьма локальные концентраторы напряжений характери­зуются тем, что объем области, занятой материалом с повышенными напряжениями, пренебрежимо мал по сравнению со всем объемом нагруженного тела. В случае размытых концентраторов напряжений объем, занятый материалом с повышенными напряжениями, со­ставляет значительную часть всего объема нагруженного тела. Таким образом, при локальной концентрации напряжений общие размеры и форма всего напряженного тела не будут существенно изменяться в случае текучести материала в зоне концентрации, тогда как при размытой концентрации напряжений они существен­но изменятся. Например, малые отверстия и скругления малого радиуса обычно считаются весьма локальными концентраторами напряжений, а крюки и шарнирные соединения серег с проушинами относятся к размытым концентраторам напряжений.

Таблица 1. Последствия концентрации напряжений

Тип концентратора напряжений	Вид нагружения	Тип материала	Вид разрушения	Коэффициент концентрации напряжений
Размытый	Статическое	хрупкий	Хрупкое разрушение	αt
		пластичный	Большая область текучести	αt (уточненный)
--//--	Циклическое	любой	Усталостное разрушение	Kf
Локальный	Статическое	хрупкий	Хрупкое разрушение	αt
		пластичный	Разрушения нет (происходит перераспределение напряжений)	1
--//--	Циклическое	любой	Усталостное разрушение	Kf

Из этой таблицы следует, что возможные последствия концентрации напряжений необходимо оценивать для всех сочетаний типов концентраторов, видов нагружения и типов материалов, за исключением одного — локальных концентраторов в пластичных материалах при действии статических нагрузок. В этих случаях локальной текучестью, как правило, можно пренебречь, и коэффи­циент концентрации можно принять равным единице. Во всех других случаях следует проанализировать возможность поврежде­ния из-за концентрации напряжений.

В последнем столбце таблицы в качестве коэффициентов кон­центрации напряжений указаны величины α_t или K_f. Коэффици­ент α_t — теоретический коэффициент концентрации упругих на­пряжений, равный по определению отношению максимального значения локального напряжения в области особенности к номи­нальному напряжению для ослабленного сечения, найденному по какой-либо простой теории без учета концентрации из-за наличия геометрической особенности.

Следует отметить, что коэффициент α_t зависит только от геометрических параметров, вида нагружения и применим только для напря­жений в упругой области. Для напряжений в пластической области он должен быть соответствующим образом уточнен.

Коэффициент K_f — эффективный коэффициент концентрации усталостных на­пряжений, равный по определению отношению действующего ус­талостного напряжения в районе особенности к номинальному ус­талостному напряжению, найденному без учета концентрации на­пряжений из-за наличия геометрической особенности.

Это опре­деление справедливо для случая многоцикловой усталости и долж­но быть соответствующим образом уточнено в случае малоцикловой усталости. Эффективный коэффициент концентрации напряжений, в отличие от теоретического, зависит от свойств материала, поэтому вводится показатель чувствительности материала к надрезам q.

Определение теоретических коэффициентов концентрации на­пряжений с помощью методов теории упругости представляет собой достаточно сложную проблему. Решения получены лишь для не­которых тел простейшей формы; среди них решения таких двумер­ных задач, как задачи о круглом или эллиптическом отверстии или вырезе в бесконечной полосе, и решение осесимметричной трехмер­ной задачи о глубокой гиперболической выточке в сплошном ци­линдрическом стержне. Однако, особенности и условия нагружения во многих случаях таковы, что концентрация напря­жений не поддается математическому исследованию. В подобных случаях для определения коэффициентов концентрации напряжений используются экспериментальные методы и расчеты по методу ко­нечных элементов. Ранее уже упоминалось, что метод конечных эле­ментов является самым распространенным методом вычисления коэффициентов концентрации напряжений. Среди других иногда используемых методов можно назвать применение механических, оптических или электрических экстензометров с малой базой, ме­тод хрупких лаковых покрытий, метод дифракции рентгеновских лучей и метод фотоупругости.