10. Элементы термодинамики

10.1. Первое начало термодинамики и его применение к изопроцессам в идеальных газах

Изопроцессы – равновесные процессы, в которых один из основных параметров сохраняется постоянным.

10.1.1. Изохорный процесс

И зохорический процесс - протекает при постоянном объеме (V = const), т.е. dV = 0. Диаграмма – изохора представлена на рис.10.1. Процесс 12 – изохорное нагревание; процесс 21 – изохорное охлаждение.

Запишем первое начало термодинамики:

.

Так как , то при изохорическом процессе, все подводимое к системе тепло идет на изменение ее внутренней энергии.

.

При этом (для 1 моля):

следовательно - изменение внутренней энергии системы пропорционально изменению ее температуры.

Для произвольной массы газа:

10.1.2. Изобарный процесс

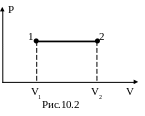
Изобарический процесс протекает при постоянном давлении (p = const). Диаграмма – изобара (рис.10.2). Процесс 12 – изобарное расширение при росте температуры; процесс 21 – изобарное сжатие при уменьшении Т.

Для изобарного процесса:

т.е. подводимое к системе тепло идет как на изменение ее внутренней энергии, так и на совершение этой системой работы.

При изобарном расширении объёма от V₁ до V₂ работа газа:

и определяется площадью прямоугольника (рис.10.1).

Используя уравнение Менделеева – Клапейрона для выбранных нами двух состояний, запишем:

и , откуда:

.

Тогда работу изобарного расширения можно найти:

(1)

Т.о., в изобарном процессе при сообщении газу массой m количества теплоты:

его внутренняя энергия увеличится на величину: ,

газ при этом совершит работу (1).

10.1.3. Изотермический процесс

Изотермический процесс. Это процесс, протекающий при постоянной температуре (T = const). Тогда

При изотермическом расширении давление не остается постоянным. Оно убывает по мере увеличения объема (рис.10.3). Поэтому для подсчета работы в данном случае нельзя пользоваться простой формулой А = РV.

В данном случае необходимо весь интервал давлений от V₁ до V₂ разбить на бесконечно малые приращения dV. В пределах столь малых изменений объема давление будет практически оставаться постоянным (P).

Для элементарной работы dA можно записать dА = РdV.

Из уравнения Менделеева – Клапейрона выразим давление:

, тогда элементарная работа: .

Вся работа: ,

.

При изотермическом расширении dU = C_vdT = 0, т.е. U = const, т.е. все подводимое к системе тепло идет на совершение этой системой работы:

.

Согласно определению теплоемкости

.

Бесконечная теплоемкость не является абсурдом. Она означает, что все подводимое тело идет на совершение работы и не приводит к повышению температуры. Причем, если тепло подводится к телу, т.е.

Q > 0, то С = +, если же происходит изотермическое сжатие, то Q < 0 и С = -.

10.1.4. Адиабатический процесс

Уравнения Пуассона

Процессы, протекающие без теплообмена или почти без теплообмена с окружающей средой называют адиабатическими или адиабатными. Примером адиабатического процесса может служить быстро протекающий процесс сжатия или расширения газа. При адиабатном процессе одновременно меняются все три параметра состояния: Р, V, T. В соответствии с этим для адиабатного процесса имеются три уравнения, связывающие попарно указанные параметры: V и Т, Р и V, Р и Т.

Найдем зависимость между давлением и объемом при адиабатическом процессе, для чего воспользуемся первым началом термодинамики . Так как , то

, а ,

т.е. работа, совершаемая системой при адиабатическом процессе, сопровождается изменением ее внутренней энергии. Но, а , тогда

.

Из уравнения состояния идеального газа для моля или киломоля , следовательно

или откуда, т.е. , а

.

Известно, что , а , тогда

;

или (1)

Следовательно, при адиабатических процессах произведение температуры на объем в степени ( - 1 ) для данной массы остается величиной постоянной.

Из полученного видно, что при адиабатическом расширении идеального газа его температура уменьшается, а при адиабатическом сжатии - увеличивается.

(1)– первое уравнение Пуассона, здесь , (т.к. , )

Из уравнения Менделеева - Клапейрона для моля или киломоля идеального газа . Подставляя значения T и V в уравнение (1), имеем

(2)

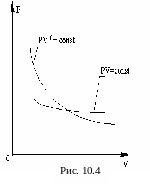
Уравнение (2) – второе уравнение Пуассона или уравнение адиабаты. Графически (в координатах p, V) адиабатический процесс можно представить адиабатой. При этом адиабата располагается более круто, чем изотерма (т.к.   1) (рис. 10.4). Это объясняется тем, что при изотермическом сжатии давление возрастает за счет изменения молекулярной плотности, т.е. за счет увеличения числа ударов молекул о стенки сосуда. При адиабатическом процессе сжатие сопровождается повышением температуры, т.е. давление возрастает не только за счет увеличения молекулярной плотности, но и за счет роста средней скорости движения молекул.