9.6. Распределение Больцмана. Барометрическая формула

Из уравнения Менделеева – Клапейрона: или

Откуда следует, в частности, что плотность воздуха уменьшается с высотой.

Выведем формулу зависимости атмосферного давления P от высоты (над уровнем моря) столба воздуха h, получившей название барометрической формулы.

И в данном случае в основу расчета будет положена некая абстракция - модель атмосферы, которая является лишь приближением к реальной атмосфере. Суть модели сводиться к следующим трем условиям:

1. (g = const) что достаточно обосновано лишь до высот около 100 км/;

2. температура вдоль столба воздуха остается постоянной т.е. рассматривается "изотермическая" атмосфера;

3. воздух состоит из молекул одного сорта (например, N₂ )

Поскольку плотность газа не остается постоянной с высотой столба, то в данном случае неприменима известная формула для давления жидкости на стенки сосуда: P=gh.

Поэтому воспользуемся таким приемом: мысленно разобьем толщу атмосферы на тонкие плоские слои воздуха (см. рис.9.6). Каждый такой слой настолько тонок, что плотность воздуха в нем остается постоянной, и вместе с тем газ, заключенный в нем, можно рассматривать как сплошную среду. Тогда приращение давления

d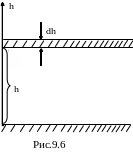 p =-gdh

Знак "-" указывает на то, что с высотой убывает давление. Поскольку на разных высотах  различно, воспользуемся полученной формулой , что позволяет записать:

dP = или (1)

Проинтегрируем обе части этого равенства (беря неопределенный интеграл):

или .

Если h = 0, то Р = Р_о, поэтому: C = P₀ и

(2)

М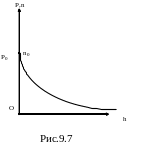 ы получили барометрическую формулу; графическая зависимость представлена на рис.9.7.

Учитывая, что n  p находим:

(3)

(3) —распределение Больцмана

Т.е. концентрация молекул с высотой столба убывает по экспоненциальному закону.

На основе зависимостей (2) и (3) разработаны простые приборы для определения высоты над уровнем моря -альтиметры. Знаменитый физик Гельмгольц еще в начале века путешествуя по Альпам останавливался и кипятил воду, чтобы по температуре кипения определить давление и по барометрической формуле рассчитать высоту гор, на которую он забрался.

7. Внутренняя энергия. Первое начало термодинамики

Внутренняя энергия тела U складывается из кинетической энергии поступательного и вращательного движения отдельных молекул этого тела, и потенциальной энергии их взаимного расположения, т.е.

U = E_к + E_кBP+E_п

В одном киломоле любого газа содержится N_А молекул (N_А - число Авогадро). Следовательно, один киломоль идеального газа имеет внутреннюю энергию, равную

Для идеального газа

Внутренняя энергия произвольной массы газа m

где  - молярная масса газа.

Таким образом, внутренняя энергия идеального газа зависит только от его объёма и давления.

Внутренняя энергия может изменяться за счет двух различных процессов: совершения над телом работы и сообщения ему количества тепла. Если при сообщении газу тепла Q он совершает над окружающими телами работу A и, кроме того, происходит приращение его внутренней энергии U, то закон сохранения энергии (в термодинамике) обуславливает равенство:

Q = U + A (2)

Это равенство носит название 1^го начала термодинамики. Следует заметить, что внутренняя энергия является однозначной функцией состояния системы частиц, т.е. определяется тройкой параметров Т, Р , V и не зависит от характера и последовательности процессов. Соответственно dU - это полный дифференциал.

Q и A не являются полным дифференциалом, их величина зависит от характера процессов, сопровождающих переход из начального состояния в конечное.