9.4. Экспериментальное подтверждение молекулярно-кинетической теории газов (опыт Штерна)

В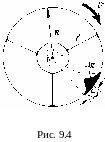 1920 г. Штерн поставил опыт, с помощью которого можно было непосредственно проверить теорию распределения молекул по скоростям и измерить скорость теплового движения молекул. Суть опыта поясняется на рис.9.4.

Два коаксиальных цилиндра вращаются как единое целое с угловой скоростью . По оси натянута платиновая проволока, покрытая тонким слоем серебра. Провод нагревается электрическим током. Температура проводки измеряется по ее электрическому сопротивлению. При температуре t = 1200⁰С атомы серебра испаряются и разлетаются по всем направлениям. Через узкую щель, прорезанную во внутреннем цилиндре, вылетает пучок атомов серебра, скорость которых направлена вдоль радиусов.

Пока атом, летящий со скоростью v, проходит расстояние между цилиндрами l, цилиндры успевают повернуться на угол , , но , следовательно,

, при l  R.

Откуда

,

где S – расстояние по окружности внешнего цилиндра от конца радиуса, проведенного через отверстие (через границу щели).

Вычисленные по результатам эксперимента значения скорости оказались близки к теоретическим результатам; кроме того, профиль сечения слоя серебра, как показано на рисунке, весьма точно соответствует распределению Максвелла молекул по скоростям. Теория получила хорошее подтверждение на опыте.

9.5.Средняя длина свободного пробега молекул

Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d. Эффективный диаметр несколько уменьшается при увеличении скорости молекул, т. е. с повышением температуры. Величина называется эффективным сечением молекулы.

Средний путь, проходимый молекулой между двумя последовательными столкновениями, называется средней длиной свободного пробега .

За 1 с молекула проходит в среднем путь, равный средней скорости . Если за 1 с в среднем происходит столкновений, то средняя длина пробега

. (1)

П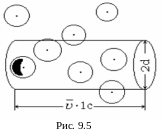 редположим, что все молекулы, кроме данной молекулы, застыли неподвижно на своих местах (рис. 9.5).

Столкновение происходит в том случае, если центр молекулы, с которой сталкивается данная молекула, лежит внутри цилиндра радиуса d. За 1с данная молекула столкнется с неподвижными молекулами столько раз, сколько находится внутри такого цилиндра длиной l = │v│∙1 c. Объем этого цилиндра составляет V = ;

число молекул, заключенных в нем (n – концентрация), следовательно, число столкновений одной молекулы с неподвижными молекулами за 1с:

.

В действительности все молекулы движутся, вследствие чего число соударений определяется средней скоростью движения молекул по отношению друг к другу. Как показывает расчет, средняя скорость относительного движения молекул в раз больше (относительно стенок сосуда). Поэтому

(2)

Подставляя (2) в (1), получим

или .

Поскольку, при постоянной температуре, n изменяется пропорционально p (p = n∙k∙T), то

Так, например, при нормальных условиях n = 2,6810²⁵ м^-3, эффективный диаметр молекулы d ~1 Å = 10^-10 м, поэтому длина свободного пробега ₀ = 210^-7 м, а при давлении 0,1 Па   0,10 м.