9.2. Вероятность и флюктуации. Скорости теплового движения частиц

Статистическая физика это раздел молекулярной физики, в котором изучаются свойства и движения не отдельных молекул (частиц), а совокупности частиц, характеризующиеся средними величинами. Одними из основных понятий статистической физики являются: вероятность и флуктуации.

Вероятность это число способов, которыми может быть реализовано данное состояние макроскопической физической системы (предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях):

w = n/N, (1)

где N - число опытов;

n - число раз получено определенное событие.

Флуктуации это случайные отклонения физических величин от их среднего значения.

Согласно молекулярно-кинетической теории молекулы идеального газа находятся в непрерывном хаотическом движении с равномерным распределением по направлениям. Скорости молекул при этом изменяются по величине. Наиболее близкой к истинному значению скорости является средняя квадратичная скорость молекул, которая для газа массой "m" находящегося в состоянии равновесия, при T = const, остаётся постоянной

,

- скорости молекул, N – число молекул.

Так как энергия молекулы , то

или (2)

Таким образом, с повышением температуры возрастает и средняя квадратичная скорость движения молекул идеального газа.

Несколько иное значение имеет средняя арифметическая скорость движения молекул:

(3)

Сравнивая (2) и (3), мы видим, что > .

Рассчитаем среднюю квадратичную скорость молекул воздуха при температуре 300К (27⁰С). Будем считать, что воздух состоит из молекул азота (N₂) с молярной массой 28 кг/кмоль, тогда

м/с.

Постоянство <v_кв> объясняется тем, что в стационарном состоянии газа устанавливается стационарное распределение молекул по скоростям, подчиняющееся статистическому закону Максвелла.

9.3. Распределение молекул (частиц) по скоростям.

Распределение Максвелла (1860г)

Средняя длина свободного пробега молекул

Возможные скорости движения молекул, заключенные в пределах от нуля до бесконечности, не равновероятны. Слишком большие по сравнению со средним квадратичным значением скорости могут реализоваться крайне редко, т.к. для этого должно реализоваться маловероятное явление, когда в результате случайных столкновений молекулы полностью передадут свою энергию одной (или нескольким) молекуле. Точно также практически исключено, что в результате соударений скорость молекулы станет равной нулю. Следовательно, очень малые и очень большие по сравнению со средним значением скорости маловероятны.

Из сказанного следует, что скорости молекул группируются в основном вблизи некоторого наиболее вероятного значения. Впервые функцию распределения молекул по скоростям получил Максвелл в 1860г. Мы воспользуемся готовым результатом и проанализируем его.

Пусть - общее число молекул, заполняющих сосуд, - число молекул, скорости которых заключены в интервале от v до v + dv. Естественно считать, что прямо пропорционально общему числу частиц и ширине интервала скоростей dv, т.е.

(1)

При этом коэффициент пропорциональности  должен зависеть от v, т.е. = f(v). Максвелл получил:

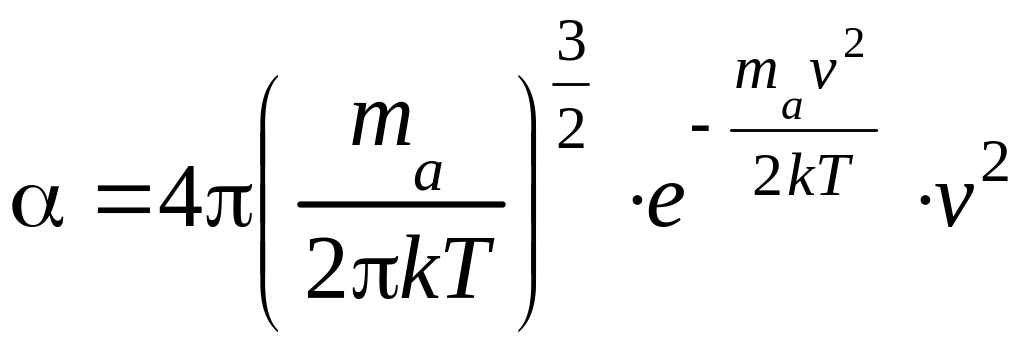. (2)

Подставляя (2) в (1) и разделив, обе части равенства, на dv получим:

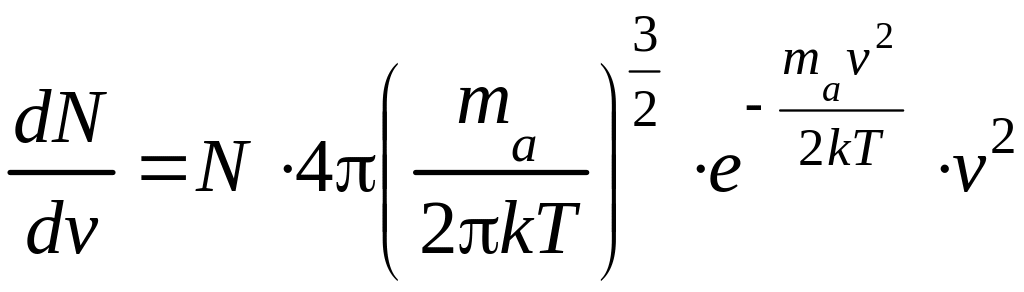
. (3)

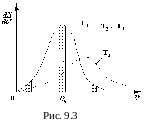
На рисунке 9.3 приведен график зависимости для двух температур.

Зависимость имеет выраженный максимум, в точке v = v_н. Значение v_н называют наивероятнейшей скоростью. Если выделить три одинаковых по ширине интервала скоростей в области малых скоростей, в окрестности наивероятнейшей скорости и в области больших скоростей, как показано на рисунке, то можно сделать следующие выводы:

1. Число молекул, имеющих малые скорости, относительно мало.

2. Число молекул, имеющих очень большие скорости, относительно мало.

3. Большая часть молекул движется со скоростями, близкими к наивероятнейшей.

Неожиданным оказывается ответ на вопрос - сколько же молекул имеют вполне определенное значение скорости, например, имеют наивероятнейшую скорость? Ответ – нисколько, нуль !!! Действительно, поскольку ширина заданного интервала скоростей равна нулю, то площадь соответствующей полоски на графике также равна нулю. Т. е., в большой массе молекул, в данное мгновение может не найтись ни одной молекулы, имеющей скорость с точно заданным значением.

Найдем значение наивероятнейшей скорости, для чего исследуем функцию на экстремум. Возьмем от функции dN/dv производную по v и приравняем ее нулю: . Для упрощения операции обозначим постоянный множитель буквой А, т.е.

.

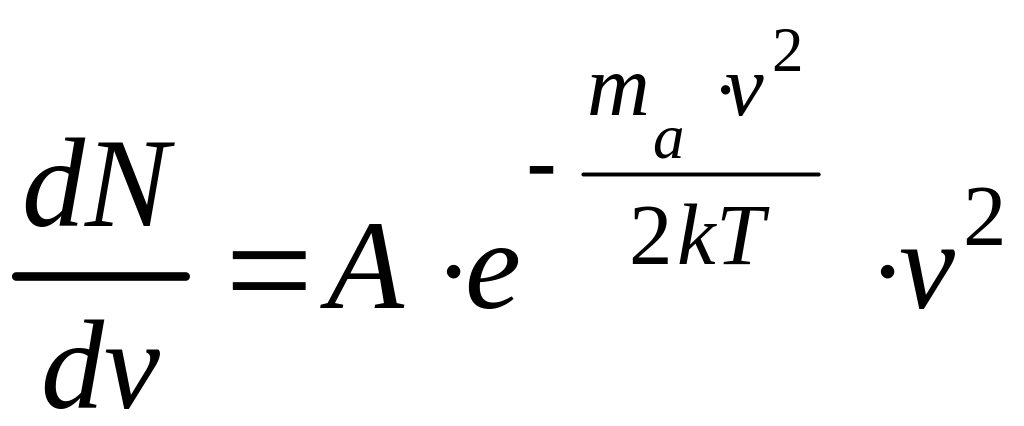Тогда

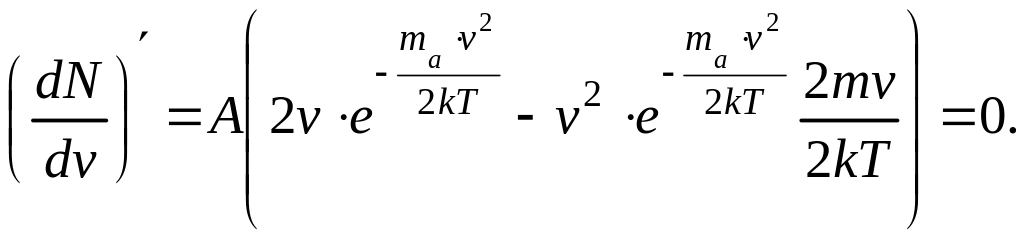
Откуда . (4)

Таким образом, получаем .

Из выражений (4) видно, что с повышением температуры Т максимум исследуемой зависимости смещается вправо (рис. 9.3). Вместе с тем максимум становится ниже. Это объясняется просто: если максимум сместился вправо, то кривая становится шире, но площадь фигуры, образованной кривой и осью «O - v» – должна быть одинаковой при Т₁ и T₂, т.к. указанные площади численно равны одной и той же величине - числу молекул внутри сосуда. Поэтому максимум для кривой при T₂ должен быть ниже чем максимум этой кривой для Т₁.

По своему численному значению наивероятнейшая скорость близка к средней квадратичной скорости, характеризуется аналогичной зависимостью от температуры.