8.4. Молекулярно-кинетическая трактовка абсолютной температуры

Для одного киломоля идеального газа можно записать:

(1)

Р = , (2)

где - суммарная кинетическая энергия поступательного движения всех молекул газа (одного моля), m –масса газа, - средняя квадратичная скорость поступательного движения молекул. Средняя квадратичная скорость: ,

- скорости молекул, N – число молекул.

Из (1) и (2) следует: RT= . Преобразуем это выражение: .

Так как - постоянная Больцмана, а = - средняя кинетическая энергия поступательного движения одной молекулы газа, то :

. (3)

Из (3) следует: - абсолютная температура T лишь постоянным множителем отличается от

Следовательно, мерой абсолютной температуры является средняя кинетическая энергия поступательного движения молекул идеального газа. Вытекающий из классической физики вывод: абсолютный нуль (-273,15 ⁰С) - температура, при которой поступательное движение молекул идеального газа замирает.

8.5.Основные газовые законы молекулярно кинетической теории

Ещё до появления молекулярно-кинетической теории газов был экспериментально установлен целый ряд законов, описывающих поведение идеальных газов.

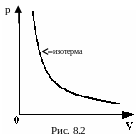
8.5.1. Закон Бойля-Мариотта

«Для данной массы газа при неизменной температуре произведение его давления на объем величина постоянная»:

pV = const при Т = const

В термодинамике процесс, происходящий при постоянной температуре, называется изотермическим. Графически он изображается в координатах p, V изотермой (рис. 8.2).

8.5.2. Закон Гей-Люссака

, (1)

т.е. для данной массы газа при постоянном давлении их объемы относятся как абсолютные температуры. Или «Для данной массы газа при постоянном давлении отношение объема к абсолютной температуре остается величиной постоянной»:

. (2)

Формулы (1) и (2) отображают закон Гей-Люссака.

В термодинамике процесс, происходящий при постоянном давлении, называется изобарическим.

Экспериментально установлено, что в этом случае объем газа изменяется по закону (при m = const, p = const)

V_t = V₀(1 + t),

г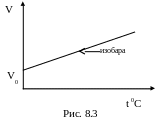 де  - коэффициент объёмного расширения - величина, которая показывает, как изменилась каждая единица начального объёма газа (при 0 ⁰С) от нагревания его на один градус при постоянном давлении

.

Такой процесс в координатах V, t он изображается изобарой (рис. 8.3).

8.5.3. Закон Шарля

, (1)

т.е. для данной массы газа при постоянном объеме их давления относятся как абсолютные температуры. Или: «Для данной массы газа при постоянном объеме отношение давления к абсолютной температуре остается величиной постоянной»

. (2)

Формулы (1) и (2) отображают закон Шарля.

В термодинамике процесс, происходящий при постоянном объеме, называется изохорическим.

Давление данной массы газа при изохорическом процессе изменяется по закону (при m = const, V = const)

,

где  - термический коэффициент давления, который показывает, на какую часть изменилась каждая единица начального давления газа (при 0 ⁰С) от нагревания его на один градус при постоянном объёме

.

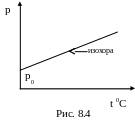Графически в координатах p, t такой процесс изображается изохорой (рис.8.4).

Так как  = , то все изобары и изохоры пересекают ось "t" в одной и той же точке. Если начало отсчёта температур сместить в эту точку, то мы перейдём к другой температурной шкале - шкале Кельвина (абсолютной шкале температур). При этом между температурой по шкале Кельвина и температурой по шкале Цельсия существует связь

T = t + 273,15.