13.5. Поверхностные явления на границе раздела двух жидкостей или жидкости и твердого тела

Е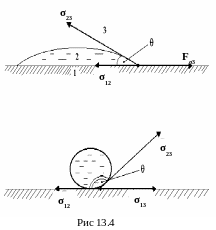 сли капля жидкости лежит на поверхности твердого тела (рис.13.4), то на единицу длины контура капли на границах твёрдое тело – газ, жидкость – газ и жидкость - твёрдое тело действуют соответственно три силы поверхностного натяжения σ₁₂, σ₁₃, σ₂₃.

Если , то капля растекается по поверхности до тех пор, пока не наступит равенство . Это случай неполного смачивания – угол θ – острый. Если же , то равновесие не может наступить и капля растекается до тех пор, пока не покроет всей его поверхности или пока не образуется мономолекулярный слой. Такой случай называется полным смачиванием.

Если , то капля будет стремиться приобрести сферическую форму.

Таким образом, при остром краевом угле ( < /2) жидкость растекается по поверхности твердого тела, смачивает его поверхность. В случае абсолютного смачивания краевой угол  = 0. При тупом краевом угле ( > /2) капля стремится стянуться в точку. Жидкость не смачивает поверхность твердого тела. Для мелких капель возможно  = π – это абсолютно не смачиваемая поверхность.

Не смачиванием объясняется такие явления как "плавание" тяжелых предметов на поверхности жидкости и "перенос воды в решете".

13.6. Капиллярные явления. Закон Жюрена

Изменение высоты уровня жидкости в узких трубах (капиллярах) или зазорах между двумя стенками получило название капиллярности.

Явления капиллярности связаны с взаимодействием между молекулами жидкости и твердого тела, с явлением смачивания. При капиллярных явлениях происходит искривление поверхности жидкости, что в свою очередь влечет к появлению дополнительного давления, под действием которого уровень жидкости в капиллярах либо поднимается, если жидкость смачивает его поверхность, либо опускается, если жидкость не смачивает поверхность капилляра. Высота подъема (опускания) жидкости в капиллярах зависит от его радиуса (рис.13.5).

П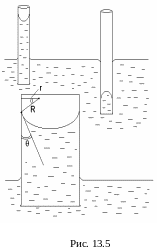 редположим, что жидкость смачивает стенки капилляра, образуется вогнутый мениск, радиус кривизны которого R. Дополнительная сила, обусловленная кривизной поверхности, направлена вверх к центру кривизны. Она создает дополнительное давление, под действием которого жидкость поднимается на высоту h. Подъем жидкости будет продолжаться до тех пор, пока дополнительное давление p не уравновесит гидростатическое давление p, т.е.

, (1)

где

R - радиус кривизны поверхности жидкости; r - радиус капилляра.

Таким образом, имеем

; ,

Откуда . (2)

(2) - отображает закон Жюрена. Чем меньше радиус r трубки, тем выше поднимается в ней столбик смачивающей жидкости или опускается столбик не смачивающей жидкости.

Капиллярные явления играют существенную роль в природе и технике. За счет капиллярных явлений происходит подъем воды из почвы по стволам деревьев и растительности, подъем влаги по стенам домов и сооружений. Осуществляются процессы, связанные с кровообращением, впитывание влаги фильтровальной бумагой, подъем керосина вдоль фитиля в керосиновых лампах и т.д.

Лекция 14

(Жидкие кристаллы и их строение. Магнитные жидкости: структура, получение, свойства, применение.

Кристаллическое состояние. Типы кристаллических решёток.)