10.7. Третье начало термодинамики (теорема Нернста)

(самостоятельно)

Согласно теореме Нернста изменение энтропии (S) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю

(13.73)

Другая эквивалентная формулировка теоремы Нернста: "При помощи последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю".

Теорема Нернста приводит к ряду важных термодинамических следствий.

В частности, коэффициент теплового расширения, изохорный коэффициент давления (dp/dT) и удельные теплоемкости c_p и c_v обращаются в нуль при T0.

Необходимо отметить, что третье начало термодинамики и вытекающие из него следствия не относятся к системам, находящимся в так называемом заторможенном состоянии. Примером такой системы является смесь веществ, между которыми хотя и возможны химические реакции, но они заторможены - скорость реакций при низких температурах очень мала.

Другим примером может служить быстро замороженный раствор, который при низкой температуре должен был бы расслоиться на две фазы, но процесс расслоения при низких температурах практически не происходит. Такие состояния во многих отношениях подобны равновесным состоянием, однако, их энтропия не обращается в нуль при абсолютной температуре стремящейся к нулю.

Лекция 11

(Реальные газы. Молекулярные силы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.)

11. Реальные газы

11.1. Реальные газы. Молекулярные силы

Как известно атомы содержат положительно заряженные ядра и электронную оболочку (электронное облако). Размеры ядер очень малы 10^-15 - 10^-14м. Радиус орбиты электрона составляет порядка 10^-10 м = 1 . При сближении молекул до расстояния около двух - трех диаметров (3 ) начинают проявляться взаимодействие зарядов ядер и электронных оболочек.

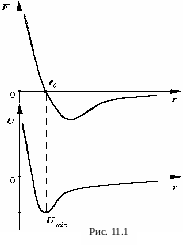П режде всего, при сближении начинают проявляться силы притяжения F<0 (рис. 11.1).

Однако когда молекулы подойдут "вплотную" друг к другу и "соприкоснутся" своими оболочками, то дальнейшее их сближение затрудняется. Между электронными оболочками возникнут огромные силы отталкивания, резко возрастающие по мере дальнейшего проникновения оболочек друг в друга. Начинают преобладать силы отталкивания F > 0. На нижнем графике дана зависимость потенциальной энергии взаимодействия молекул от расстояния между их центрами U(r). Когда результирующая сила межмолекулярного взаимодействия равна нулю (при r = r₀) потенциальная энергия минимальна: W_{p min}<0, т.е. для удаления молекул друг от друга необходимо, чтобы внешние силы, совершили работу.

Между тремя основными агрегатными состояниями имеется значительное расхождение в величине энергии межмолекулярного взаимодействия. Так, например, для:

1) газов кТ >> W_{p min};

2) кристаллических твердых тел кТ << W_{p min};

3) жидкостей кТ  W_{p min}.

Движение молекул и структура вещества существенно зависят от соотношения энергии теплового движения и потенциальной энергии взаимодействия между молекулами.