Современные проблемы физики / PhysicalReviewpdf / Trubetskov-3

TURBULENCE

AND DETERMINISTIC

CHAOS

D. I. TRUBETSKOV

The possibility to explain the turbulence appearance in fluid in the context of modern concepts about deterministic chaos is discussed. The main features of developed turbulence and the Feigenbaum scenario (infinite set of period doubling) of transition to turbulence are considered.

й·ТЫК‰‡ВЪТfl ‚УБПУКМУТЪ¸ У·˙flТМЛЪ¸ ‚УБМЛНМУ‚ВМЛВ ЪЫ ·ЫОВМЪМУТЪЛ ‚ КЛ‰НУТЪЛ Т ФУБЛˆЛИ ТУ‚ ВПВММ˚ı Ф В‰ТЪ‡‚- ОВМЛИ У ‰ВЪВ ПЛМЛ У- ‚‡ММУП ı‡УТВ. к‡ТТПУЪ-ВМ˚ УТМУ‚М˚В ˜В Ъ˚‡Б‚ЛЪУИ ЪЫ ·ЫОВМЪМУТЪЛ Л ТˆВМ‡ ЛИ оВИ„ВМ·‡- ЫП‡ (·ВТНУМВ˜М˚И Н‡Т- Н‡‰ Ы‰‚УВМЛИ ФВ ЛУ‰‡) ФВ ВıУ‰‡ Н ЪЫ ·ЫОВМЪМУТЪЛ.

© í۷ˆÍÓ‚ Ñ.à., 1998

нмкЕмгЦзнзйлнъ а СЦнЦкеазакйЗАззхв пАйл

С. а. нкмЕЦсдйЗ

л‡ ‡ЪУ‚ТНЛИ „УТЫ‰‡ ТЪ‚ВММ˚И ЫМЛ‚В ТЛЪВЪ ЛП. з.Й. уВ М˚¯В‚ТНУ„У

ЗЗЦСЦзаЦ

“нЫ ·ЫОВМЪМУТЪ¸ – fl‚ОВМЛВ, НУЪУ УВ ‚ТЪ В˜‡ВЪТfl, ıУЪЛП П˚ ЪУ„У ЛОЛ МВЪ, ‚ ˜ ВБ‚˚˜‡ИМУ ‡БМУУ·-‡БМ˚ı ЫТОУ‚Лflı, Н‡Н ‚ Ф ЛНО‡‰М˚ı (М‡Ф ЛПВ , ‚ ‡˝ У‰ЛМ‡ПЛНВ, „Л‰ ‡‚ОЛНВ, ‚УВММУ-ПУ ТНУП ‰ВОВ Л ıЛПЛ˜ВТНУП Ф УЛБ‚У‰ТЪ‚В), Ъ‡Н Л ‚ ВТЪВТЪ‚ВММ˚ı ТЛЪЫ‡ˆЛflı (‚ „ВУЩЛБЛНВ, УТУ·ВММУ ‚ ПВЪВУ УОУ„ЛЛ Л УНВ‡МУ„ ‡ЩЛЛ, Л ‚ ‡ТЪ УЩЛБЛНВ) …

З Т‚ВЪВ ˝ЪУ„У МВ fl‚Оfl˛ЪТfl МВУКЛ‰‡ММ˚ПЛ У„-УПМ˚В ЫТЛОЛfl, Ы‰ВОflВП˚В ‚У ‚ТВП ПЛ В ЩЫМ‰‡ПВМ- Ъ‡О¸М˚П ЛТТОВ‰У‚‡МЛflП ЪЫ ·ЫОВМЪМУТЪЛ… й‰М‡НУ Т ˜ЛТЪУ ЪВУ ВЪЛ˜ВТНУИ ТЪУ УМ˚ ЛТТОВ‰У‚‡ЪВОЛ ТЪУОНМЫОЛТ¸ Т ЛТНО˛˜ЛЪВО¸М˚ПЛ Ъ Ы‰МУТЪflПЛ ПВЪУ‰У‚… Л ‚УБМЛНОУ ФУМЛП‡МЛВ ЪУ„У, ˜ЪУ Ф У·ОВП‡ ЪЫ ·ЫОВМЪМУТЪЛ, ‚ТВ„‰‡ Т˜ЛЪ‡‚¯‡flТfl Ъ Ы‰МУИ, ‚ ‰ВИТЪ‚ЛЪВО¸МУТЪЛ ˜ ВБ‚˚˜‡ИМУ Ъ Ы‰М‡. иУ˝ЪУПЫ‡Т¯Л ЛОЛТ¸ ‚ ВПВММ˚В ПВ НЛ ТЫ˘ВТЪ‚ВММУ„У Ф У„ ВТТ‡ ‚ ФУМЛП‡МЛЛ ˝ЪУ„У fl‚ОВМЛfl”. н‡Н М‡˜Л- М‡ВЪ Т‚У˛ ТЪ‡Ъ¸˛ У МВНУЪУ ˚ı М‡Ф ‡‚ОВМЛflı ‡Б- ‚ЛЪЛfl ЪВУ ЛЛ ЪЫ ·ЫОВМЪМУТЪЛ ‡М„ОЛИТНЛИ ЩЛБЛН Й. еУЩЩ‡Ъ [1, Т. 49–50].

й‰М‡НУ ТУ·˚ЪЛfl, Ф УЛБУ¯В‰¯ЛВ ‚ ЩЛБЛНВ ‚ ФУТОВ‰МЛВ ‰ВТflЪЛОВЪЛfl, ‰‡ОЛ МУ‚˚И ЪУО˜УН ‡Б‚ЛЪЛ˛ ЪВУ ЛЛ ЪЫ ·ЫОВМЪМУТЪЛ. мФУПflМЫЪ˚В ТУ·˚ЪЛfl Т‚fl- Б‡М˚ Т УЪН ˚ЪЛВП ‰ВЪВ ПЛМЛ У‚‡ММУ„У ı‡УТ‡, НУЪУ-˚И ФУfl‚ОflВЪТfl ‚ ТЛТЪВП‡ı Т П‡О˚П ˜ЛТОУП ТЪВФВМВИ Т‚У·У‰˚ Л Ф Л УЪТЫЪТЪ‚ЛЛ ТОЫ˜‡ИМУТЪВИ (ТП., М‡Ф ЛПВ , [2]). й‰МУ ЛБ ‚УБПУКМ˚ı Н‡˜ВТЪ‚ВММ˚ı У·˙flТМВМЛИ ‚УБМЛНМУ‚ВМЛfl ‰ВЪВ ПЛМЛ У‚‡ММУ„У ı‡УТ‡ ТУТЪУЛЪ ‚ ТОВ‰Ы˛˘ВП. иВ ВМВТВПТfl ‚ Щ‡БУ‚УВ Ф УТЪ ‡МТЪ‚У – У·˚˜МУВ Ф УТЪ ‡МТЪ‚У НУУ ‰ЛМ‡Ъ Л Ф УТЪ ‡МТЪ‚У ТНУ УТЪВИ (ЛОЛ ЛПФЫО¸ТУ‚) ТЛТЪВП˚. о‡БУ‚УВ Ф УТЪ ‡МТЪ‚У МВФ В ˚‚МУ, ФУ˝ЪУПЫ М‡- ˜‡О¸М˚В ЫТОУ‚Лfl ‰‚ЛКВМЛfl ТЛТЪВП˚ Б‡‰‡˛ЪТfl Л ‡- ˆЛУМ‡О¸М˚ПЛ ˜ЛТО‡ПЛ – ·ВТНУМВ˜МУИ МВФВ ЛУ‰Л- ˜ВТНУИ ФУТОВ‰У‚‡ЪВО¸МУТЪ¸˛ ˆЛЩ . н‡НЛП У· ‡БУП, ФУ˜ЪЛ О˛·‡fl ЪУ˜Н‡ Щ‡БУ‚У„У Ф УТЪ ‡МТЪ‚‡ ЫКВ ТУ- ‰В КЛЪ ‚ ТВ·В ТОЫ˜‡ИМУТЪ¸ (ТОУ‚У “ФУ˜ЪЛ” УЪПВ˜‡ВЪ ТЫ˘ВТЪ‚У‚‡МЛВ ‡ˆЛУМ‡О¸М˚ı ˜ЛТВО, МУ Ъ‡НЛı МВТОЫ˜‡ИМ˚ı ЪУ˜ВН ‚ Щ‡БУ‚УП Ф УТЪ ‡МТЪ‚В У˜ВМ¸ П‡- ОУ). ЦТОЛ П˚ ЪВФВ ¸ ФУПВТЪЛП ‚ Щ‡БУ‚УВ Ф УТЪ ‡М- ТЪ‚У ‰ЛМ‡ПЛ˜ВТНЫ˛ ТЛТЪВПЫ (‰‡КВ У˜ВМ¸ Ф УТЪЫ˛), ЪУ ВВ УО¸ ТУТЪУЛЪ ‚ Ф В‚ ‡˘ВМЛЛ ТОЫ˜‡ИМУТЪЛ М‡- ˜‡О¸М˚ı ЫТОУ‚ЛИ ‚ П‡Н УТНУФЛ˜ВТНЫ˛ ТОЫ˜‡ИМУТЪ¸ ‰‚ЛКВМЛfl ТЛТЪВП˚. и Л ТЫ˘ВТЪ‚У‚‡МЛЛ ‚ ТЛТЪВПВ ОУН‡О¸МУИ МВЫТЪУИ˜Л‚УТЪЛ, НУ„‰‡ ·ОЛБНЛВ Ъ ‡ВНЪУ-ЛЛ ‡ТıУ‰flЪТfl ˝НТФУМВМˆЛ‡О¸МУ, М‡ Н‡НУП-ЪУ ˝Ъ‡ФВ ‰‚ЛКВМЛВ УФ В‰ВОflВЪТfl ‰ВЪ‡ОflПЛ М‡˜‡О¸М˚ı

ЫТОУ‚ЛИ Л ТЛО¸МУ Б‡‚ЛТЛЪ УЪ МЛı. и В‰ФУОУКЛП, ˜ЪУ Щ‡БУ‚УВ Ф УТЪ ‡МТЪ‚У У„ ‡МЛ˜ВМУ. нУ„‰‡ ‡МУ ЛОЛ ФУБ‰МУ ‡Б·ВК‡‚¯ЛВТfl Ъ ‡ВНЪУ ЛЛ ‚В МЫЪТfl ‰ Ы„ Н ‰ Ы„Ы. а Ъ‡Н ·Ы‰ВЪ ПМУ„У ‡Б. и УЛТıУ‰ЛЪ Н‡Н ·˚ ФВ-ВПВ¯Л‚‡МЛВ Щ‡БУ‚У„У Ф УТЪ ‡МТЪ‚‡, Ф Уfl‚Оfl˛˘В- ВТfl ‚ ı‡УЪЛ˜ВТНУП ‰‚ЛКВМЛЛ Щ‡БУ‚˚ı Ъ ‡ВНЪУ ЛИ.

й· ‡БУП ı‡УТ‡ ‚ Щ‡БУ‚УП Ф УТЪ ‡МТЪ‚В fl‚ОflВЪТfl ТЪ ‡ММ˚И ‡ЪЪ ‡НЪУ – У·˙ВНЪ ‚ Щ‡БУ‚УП Ф УТЪ ‡М- ТЪ‚В, Н НУЪУ УПЫ ТЪ ВПflЪТfl ‚ТВ ЛОЛ ФУ˜ЪЛ ‚ТВ Ъ ‡ВНЪУ ЛЛ Л М‡ НУЪУ УП УМЛ МВЫТЪУИ˜Л‚˚. зВ ПВМВВ Ы‰Л‚ЛЪВО¸М˚П, ˜ВП Т‡ПУ УЪН ˚ЪЛВ ‰ВЪВ ПЛМЛ У- ‚‡ММУ„У ı‡УТ‡, УН‡Б‡ОУТ¸ ЪУ, ˜ЪУ ‚ ı‡УТВ ВТЪ¸ ФУ fl- ‰УН, ЪУ, ˜ЪУ ТЫ˘ВТЪ‚Ы˛Ъ ЫМЛ‚В Т‡О¸М˚В ТˆВМ‡ ЛЛ ‚УБМЛНМУ‚ВМЛfl ı‡УТ‡.

е˚ТО¸ Т‚flБ‡Ъ¸ ЪЫ ·ЫОВМЪМУТЪ¸ Л ‰ВЪВ ПЛМЛ У- ‚‡ММ˚И ı‡УТ ‚˚„Оfl‰ЛЪ ‚ФУОМВ ВТЪВТЪ‚ВММУИ, Л ˝ЪУПЫ ФУТ‚fl˘ВМУ ·УО¸¯УВ ˜ЛТОУ ‡·УЪ.

мзаЗЦклДгъзхв иЦкЦпйС д пДйлм ий оЦвЙЦзЕДмем

З 1976 „У‰Ы ‡ПВ ЛН‡МТНЛИ ТФВˆЛ‡ОЛТЪ ‚ У·О‡ТЪЛ П‡ЪВП‡ЪЛ˜ВТНУИ Л ЪВУ ВЪЛ˜ВТНУИ ЩЛБЛНЛ еЛЪ˜ВО оВИ„ВМ·‡ЫП Т‰ВО‡О УЪН ˚ЪЛВ, ТУТЪУfl˘ВВ ‚ ЪУП, ˜ЪУ ТˆВМ‡ ЛИ ФВ ВıУ‰‡ Н ı‡УТЫ ˜В ВБ ·ВТНУМВ˜М˚И Н‡Т- Н‡‰ ·ЛЩЫ Н‡ˆЛИ1 Ы‰‚УВМЛfl ФВ ЛУ‰‡ ЫМЛ‚В Т‡ОВМ ‰Оfl ·УО¸¯У„У НО‡ТТ‡ ‰ЛМ‡ПЛ˜ВТНЛı ТЛТЪВП.

уЪУ ЫКВ ·˚ОУ ЛБ‚ВТЪМУ Н ЪУПЫ ‚ ВПВМЛ Л ПУ„ОУ ТЪ‡Ъ¸ ЛТЪУ˜МЛНУП ‚‰УıМУ‚ВМЛfl ‰Оfl оВИ„ВМ·‡ЫП‡? ЗУ-ФВ ‚˚ı, В˘В ‚ 1971 „У‰Ы ·˚ОУ У·М‡ ЫКВМУ ЛМЪВ-ВТМУВ Т‚УИТЪ‚У В¯ВМЛИ Ы ‡‚МВМЛfl ЪЛФ‡ xn + 1 = = λf(xn): Ф Л ЛБПВМВМЛЛ Ф‡ ‡ПВЪ ‡ λ ТЫ˘ВТЪ‚Ы˛˘ВВ ФВ ЛУ‰Л˜ВТНУВ В¯ВМЛВ, ЛПВ˛˘ВВ ФВ ЛУ‰ T, ЪВ flВЪ ЫТЪУИ˜Л‚УТЪ¸, ‡ ЫТЪУИ˜Л‚˚П ТЪ‡МУ‚ЛЪТfl В¯ВМЛВ Т ФВ ЛУ‰УП 2T, Á‡ÚÂÏ 4T Л Ъ.‰. аМЪВ ‚‡О ЛБПВМВМЛfl Ф‡ ‡ПВЪ ‡ λ, ‚ Ф В‰ВО‡ı НУЪУ У„У ˆЛНО ФВ ЛУ‰‡ 2n ЫТЪУИ˜Л‚, ·˚ТЪ У ТЫК‡ВЪТfl. ЗТВ БМ‡˜ВМЛfl λ, ‚ НУЪУ-˚ı Ф УЛТıУ‰ЛЪ ·ЛЩЫ Н‡ˆЛfl Ы‰‚УВМЛfl ФВ ЛУ‰‡, Т„Ы˘‡˛ЪТfl Н МВНУЪУ УПЫ БМ‡˜ВМЛ˛ λ = λÍ . ä‡Í ÚÓθÍÓ λ ÒÚ‡ÌÓ‚ËÚÒfl ·Óθ¯Â λÍ , ‚МЫЪ Л МВНУЪУ УИ У·О‡ТЪЛ Щ‡БУ‚У„У Ф УТЪ ‡МТЪ‚‡ (У„ ‡МЛ˜ВММУИ, Ф ЛЪfl„Л‚‡˛˘ВИ) УН‡Б˚‚‡ВЪТfl ·ВТНУМВ˜МУВ ˜ЛТОУ МВЫТЪУИ˜Л‚˚ı ˆЛНОУ‚ (‚ ЪУП ˜ЛТОВ Л ·ВТНУМВ˜МУ„У Т ФВ ЛУ‰УП T = 2 ). ЗТОВ‰ Б‡ ˝ЪЛП ТОУКМ˚П У· ‡БУ- ‚‡МЛВП Т ‡БЫ ‚УБМЛН‡ВЪ ı‡УЪЛ˜ВТНЛИ (ТЪ ‡ММ˚И) ‡Ъ- Ъ ‡НЪУ .

ЗУ-‚ЪУ ˚ı, Н ЪУПЫ ‚ ВПВМЛ ФУfl‚ЛОЛТ¸ ТУПМВМЛfl

‚ТˆВМ‡ ЛЛ ‚УБМЛНМУ‚ВМЛfl ЪЫ ·ЫОВМЪМУТЪЛ ФУ г‡М- ‰‡Ы. иУflТМЛП ТН‡Б‡ММУВ. аБ‚ВТЪМУ, ˜ЪУ ‚ УФ В‰В- ОВММ˚ı ЫТОУ‚Лflı ЪВ˜ВМЛВ КЛ‰НУТЪЛ ·˚‚‡ВЪ ‡БМ˚П:

‚У‰МЛı – У‚М˚П, ЫТЪУИ˜Л‚˚П, В„ЫОfl М˚П ЛОЛ, Н‡Н „У‚У flЪ, О‡ПЛМ‡ М˚П, ‡ ‚ ‰ Ы„Лı – МВ У‚М˚П,

1 ЕЛЩЫ Н‡ˆЛfl – П‡ЪВП‡ЪЛ˜ВТНЛИ У· ‡Б, ТУУЪ‚ВЪТЪ‚Ы˛˘ЛИ ФВ ВТЪ УИНВ ı‡ ‡НЪВ ‡ ‰‚ЛКВМЛfl В‡О¸МУИ (ЩЛБЛ˜ВТНУИ, ·ЛУОУ„Л˜ВТНУИ Л Ъ.‰.) ТЛТЪВП˚. е‡ЪВП‡ЪЛ˜ВТНЛ ·ЛЩЫ Н‡- ˆЛfl ВТЪ¸ ТПВМ‡ ЪУФУОУ„Л˜ВТНУИ ТЪ ЫНЪЫ ˚ ‡Б·ЛВМЛfl Щ‡- БУ‚У„У Ф УТЪ ‡МТЪ‚‡ ‰ЛМ‡ПЛ˜ВТНУИ ТЛТЪВП˚ М‡ Ъ ‡ВНЪУ-ЛЛ Ф Л П‡ОУП ЛБПВМВМЛЛ ВВ Ф‡ ‡ПВЪ У‚.

МВЫТЪУИ˜Л‚˚П, МВ В„ЫОfl М˚П – ЪЫ ·ЫОВМЪМ˚П2. дТЪ‡ЪЛ, ı‡ ‡НЪВ О‡ПЛМ‡ МУ„У ЪВ˜ВМЛfl ОВ„НУ ФУОЫ- ˜‡ВЪТfl ЛБ В¯ВМЛfl Ы ‡‚МВМЛИ, ‡ ‚УЪ МВФ В‰ТН‡БЫВПУТЪ¸ ЪЫ ·ЫОВМЪМУ„У УФЛТ‡Ъ¸ МВФ УТЪУ. лЫ˘ВТЪ‚ЫВЪ О˛·УФ˚ЪМУВ ‚УТФУПЛМ‡МЛВ М‡ ˝ЪЫ ЪВПЫ, Ф ЛМ‡‰ОВ- К‡˘ВВ ‚ТВ ЪУПЫ КВ ‡М„ОЛИТНУПЫ ЩЛБЛНЫ еУЩЩ‡ЪЫ [1, Т. 63]. “З 1961 „У‰Ы ‚ е‡ ТВОВ ·˚О Ф У‚В‰ВМ ‚‡К- М˚И НУООУН‚ЛЫП ФУ ТОЫ˜‡˛ УЪН ˚ЪЛfl аМТЪЛЪЫЪ‡ ТЪ‡ЪЛТЪЛ˜ВТНЛı ПВЪУ‰У‚ ЪЫ ·ЫОВМЪМУТЪЛ. щЪУ ·˚О ПУИ ФВ ‚˚И УФ˚Ъ ПВК‰ЫМ‡ У‰М˚ı НУМЩВ ВМˆЛИ, Л fl ФУТЪЛ„‡О В„У Т ·УО¸¯УИ ‰УОВИ ‚УОМВМЛfl Л М‡‰ВК- ‰˚. н‡П ·˚ОЛ н. д‡ П‡М, ‡ Ъ‡НКВ А.з. дУОПУ„У У‚ Л СК. н˝ИОУ (‚ТВ Ъ УВ ‚МВТОЛ УТМУ‚УФУО‡„‡˛˘ЛИ ‚НО‡‰ ‚ „Л‰ У‰ЛМ‡ПЛНЫ. – è ËϘ. ‡‚ÚÓ ‡). ь ‚ТФУПЛМ‡˛, ˜ЪУ д‡ П‡М ‚ Т‚УВП ‚˚ТЪЫФОВМЛЛ М‡ УЪН ˚- ЪЛЛ НУМЩВ ВМˆЛЛ ТН‡Б‡О, ˜ЪУ, НУ„‰‡ УМ М‡НУМВˆ Ф В‰ТЪ‡МВЪ ФВ В‰ лУБ‰‡ЪВОВП, ФВ ‚УВ, У ˜ВП УМ ФУ- Ф УТЛЪ, ·Ы‰ВЪ ‡ТН ˚ЪЛВ Ъ‡ИМ ЪЫ ·ЫОВМЪМУТЪЛ”. й·˙flТМВМЛВ, Ф В‰ОУКВММУВ г¸‚УП С‡‚Л‰У‚Л˜ВП г‡М‰‡Ы, ТУТЪУЛЪ ‚ ЪУП, ˜ЪУ ‚ ЪЫ ·ЫОВМЪМУП ЪВ˜ВМЛЛ ‚УБМЛН‡ВЪ ПМУ„У ‡БОЛ˜М˚ı МВБ‡‚ЛТЛП˚ı НУОВ·‡- МЛИ Т МВТУЛБПВ ЛП˚ПЛ ˜‡ТЪУЪ‡ПЛ. и Л ˝ЪУП Н‡К- ‰УВ ЛБ НУОВ·‡МЛИ ПУКВЪ ·˚Ъ¸ Ф УТЪ˚П, МУ Лı ТУ‚У- НЫФМУТЪ¸ Ф Л‚У‰ЛЪ Н МВФ В‰ТН‡БЫВПУИ ТОУКМУТЪЛ ‰‚ЛКВМЛfl.

З ‡·УЪВ С. к˛˝Оfl (о ‡МˆЛfl) Л о. н‡НВМТ‡ (зЛ- ‰В О‡М‰˚) (1971) ‚УБМЛНМУ‚ВМЛВ ЪЫ ·ЫОВМЪМУТЪЛ Т‚flБ˚‚‡ОУТ¸ Т ФУfl‚ОВМЛВП ТЪ ‡ММУ„У ‡ЪЪ ‡НЪУ ‡, НУЪУ ˚И ‚УБМЛН‡О ФУТОВ МВ·УО¸¯У„У ˜ЛТО‡ (Ъ Вı) ·ЛЩЫ Н‡ˆЛИ. з‡ФУПМЛП, ˜ЪУ ТЪ ‡ММ˚П ‡ЪЪ ‡НЪУ-УП М‡Б˚‚‡ВЪТfl У·˙ВНЪ ‚ Щ‡БУ‚УП Ф УТЪ ‡МТЪ‚В, Н НУЪУ УПЫ ТЪ ВПflЪТfl ‚ТВ ЛОЛ ФУ˜ЪЛ ‚ТВ Ъ ‡ВНЪУ ЛЛ Л

М‡ НУЪУ УП УМЛ МВЫТЪУИ˜Л‚˚.

к‡БЫПВВЪТfl, ФУfl‚ЛО‡Т¸ Л‰Вfl Т‚flБ‡Ъ¸ МВФ В ˚‚- М˚И ФВ ВıУ‰ Н ЪЫ ·ЫОВМЪМУТЪЛ Т ‚УБПУКМУТЪ¸˛ В‡- ОЛБ‡ˆЛЛ ‚ ЪВ˜ВМЛЛ ·ВТНУМВ˜МУ„У Н‡ТН‡‰‡ ·ЛЩЫ Н‡- ˆЛИ Ы‰‚УВМЛfl ФВ ЛУ‰‡.

å.оВИ„ВМ·‡ЫП ‡М‡ОЛБЛ У‚‡О Ы ‡‚МВМЛВ xn + 1 =

=λxn(1 − xn). йМ ıУЪВО ЛБЫ˜ЛЪ¸ НУПФОВНТМ˚В ‡М‡ОЛЪЛ˜ВТНЛВ Т‚УИТЪ‚‡ ЩЫМНˆЛИ, ФУ УК‰‡ВП˚ı Ъ‡НЛП УЪУ· ‡КВМЛВП. м ‡‚МВМЛВ ‡М‡ОЛЪЛ˜ВТНЛ МВ В¯‡-

ОУТ¸, Л оВИ„ВМ·‡ЫП Б‡МflОТfl ˜ЛТОВММ˚ПЛ ‡Т˜ВЪ‡ПЛ БМ‡˜ВМЛИ Ф‡ ‡ПВЪ ‡ λ, Ф Л НУЪУ ˚ı Ф УЛТıУ‰ЛОУ Н‡К‰УВ Ы‰‚УВМЛВ. йМ ЛТФУО¸БУ‚‡О Н‡ П‡ММ˚И Н‡О¸НЫОflЪУ , Л ФУ˝ЪУПЫ ‡Т˜ВЪ˚ ‰ОЛОЛТ¸ ‰УО„У. оВИ„ВМ·‡ЫП Б‡ПВЪЛО, ˜ЪУ БМ‡˜ВМЛfl Ф‡ ‡ПВЪ У‚, ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ Н‡К‰УПЫ Ы‰‚УВМЛ˛, ТıУ‰flЪТfl Н‡Н „ВУПВЪ Л˜ВТН‡fl Ф У„ ВТТЛfl. щЪУ ·˚ОУ Ы‰Л‚ЛЪВО¸МУ: Н‡К‰˚И ФУТОВ‰Ы˛˘ЛИ ¯‡„ ПУКМУ ·˚ОУ Т˜ЛЪ‡Ъ¸ ‡М‡ОЛЪЛ˜ВТНЛ. бМ‡ПВМ‡ЪВО¸ Ф У„ ВТТЛЛ ЪВФВ ¸ МУ-

ТЛЪ М‡Б‚‡МЛВ ФУТЪУflММУИ оВИ„ВМ·‡ЫП‡, В„У У·УБМ‡- ˜‡˛Ъ ·ЫН‚УИ δ, УМ ‡‚ВМ 4,6692…

2 нВ, НЪУ ОВЪ‡О М‡ Т‡ПУОВЪ‡ı М‡ ‰‡О¸МЛı Ъ ‡ТТ‡ı, ФУПМflЪ КВОВБМ˚И „УОУТ НУП‡М‰Л ‡ НУ ‡·Оfl: “ЙУТФУ‰‡, Ф ЛТЪВ„- МЛЪВ, ФУК‡ОЫИТЪ‡, ВПМЛ. е˚ ФУФ‡ОЛ ‚ ЪЫ ·ЫОВМЪМ˚И ФУЪУН”. а ‚˚ ‚ТНУ В У˘Ы˘‡ВЪВ М‡ ТВ·В ˝ЪУ ФУФ‡‰‡МЛВ.

аБ‚ВТЪМ˚И ‡ПВ ЛН‡МТНЛИ П‡ЪВП‡ЪЛН л. лПВИО ФУ‰ТН‡Б‡О оВИ„ВМ·‡ЫПЫ, ˜ЪУ Ы‰‚УВМЛfl ‚ В¯ВМЛЛ ВТЪ¸ Л Ы Ы ‡‚МВМЛfl xn + 1 = λsin(nxn). кВБЫО¸Ъ‡Ъ ·˚О ЪУЪ КВ: ‚МУ‚¸ ФУfl‚ЛО‡Т¸ „ВУПВЪ Л˜ВТН‡fl Ф У„ ВТТЛfl ТУ БМ‡˜ВМЛВП δ = 4,6692…

ᇉ‡˜‡. èÓÔ Ó·ÛÈÚÂ Ò ÔÓÏÓ˘¸˛ ÏËÍ Ó͇θÍÛÎflÚÓ ‡ Ô ÓÈÚË ÔÛÚ¸ îÂÈ„ÂÌ·‡Ûχ. ç‡È‰ËÚ ҇ÏË δ.

lj‡О¸МВИ¯ВП УН‡Б‡ОУТ¸, ˜ЪУ ФУТОВ‰У‚‡ЪВО¸- МУТЪ¸ Ы‰‚УВМЛИ У·О‡‰‡ВЪ Т‚УИТЪ‚УП ЫМЛ‚В Т‡О¸МУТЪЛ, НУЪУ УВ МВ Б‡‚ЛТЛЪ УЪ НУМН ВЪМ˚ı УТУ·ВММУТЪВИ ТЛТЪВП˚, ‡ ‚У ПМУ„Лı ТОЫ˜‡flı Л УЪ ‡БПВ МУТЪЛ Щ‡- БУ‚У„У Ф УТЪ ‡МТЪ‚‡. З ˜ВП КВ Б‡НО˛˜‡ВЪТfl ˝Ъ‡ ЫМЛ- ‚В Т‡О¸МУТЪ¸? З ЪУП, У ˜ВП М‡ФЛТ‡МУ ‚˚¯В, ‚ ЪУП, ˜ЪУ оВИ„ВМ·‡ЫП “‚˚Ы‰ЛО” „ВУПВЪ Л˜ВТНЫ˛ Ф У-

„ ÂÒÒ˲: ‡ÒÒÚÓflÌË ÏÂÊ‰Û Á̇˜ÂÌËflÏË Ô‡ ‡ÏÂÚ ‡

λn , Ô Ë ÍÓÚÓ ÓÏ Óʉ‡ÂÚÒfl ˆËÍÎ Ô ËÓ‰‡ 2n, Л БМ‡- ˜ВМЛВП λÍ , ‚ТОВ‰ Б‡ НУЪУ ˚П ‚ ТЛТЪВПВ ‚УБМЛН‡ВЪ ı‡УТ, Ы‰У‚ОВЪ‚У flВЪ ЫТОУ‚Л˛ (λÍ − λn) = const δ−n, „‰В δ = 4,6692… – ЫМЛ‚В Т‡О¸М‡fl ФУТЪУflММ‡fl оВИ- „ВМ·‡ЫП‡. (и ‡‚‰‡, ˝ЪУ ОЛ¯¸ У‰МУ Ф Уfl‚ОВМЛВ ЪУ„У, ˜ЪУ М‡Б˚‚‡˛Ъ ЪВУ ЛВИ ЫМЛ‚В Т‡О¸МУТЪЛ, МУ П˚ У„-‡МЛ˜ЛПТfl ТН‡Б‡ММ˚П.) щЪУ, ‚ ˜‡ТЪМУТЪЛ, УБМ‡˜‡ВЪ, ˜ЪУ ВТОЛ ‚ ˝НТФВ ЛПВМЪВ У·М‡ ЫКВМ˚ МВТНУО¸НУ ФВ ‚˚ı Ы‰‚УВМЛИ (‚ ТФВНЪ В ПУ˘МУТЪЛ ЛП ТУУЪ‚ВЪТЪ‚ЫВЪ ФУfl‚ОВМЛВ ‰ЛТН ВЪМ˚ı ФЛНУ‚ М‡ ˜‡ТЪУЪ‡ı

f0/2, f0/4 Ë Ú.‰., „‰Â f0 – ˜‡ÒÚÓÚ‡ ÓÒÌÓ‚ÌÓ„Ó Ô ËÓ‰Ë-

˜ВТНУ„У ‰‚ЛКВМЛfl), ЪУ ПУКМУ Ф В‰ТН‡Б‡Ъ¸ БМ‡˜ВМЛВ λÍ , ФУТОВ ‰УТЪЛКВМЛfl НУЪУ У„У УК‰‡ВЪТfl ı‡УТ.

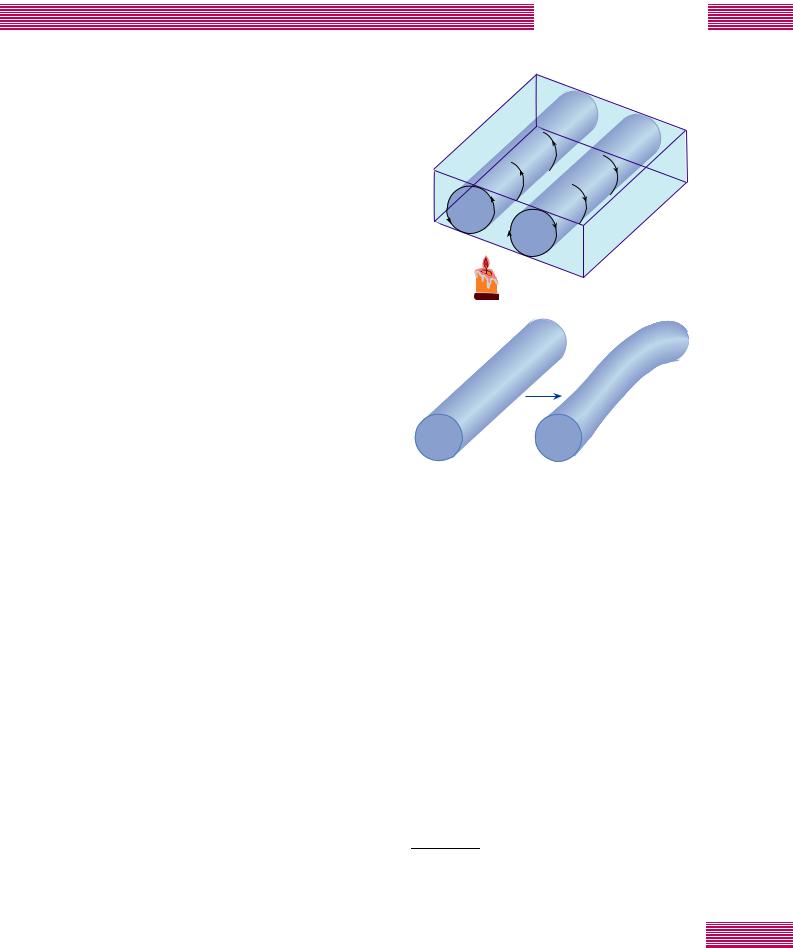
Ç1980 „У‰Ы ФУfl‚ЛОТfl ˝НТФВ ЛПВМЪ гЛ·‡ıВ ‡ Л е‡Ы˝ ‡ ФУ НУМ‚ВНˆЛЛ КЛ‰НУТЪЛ, ‚ НУЪУ УП ФУН‡Б˚- ‚‡ОУТ¸, ˜ЪУ ЪВФОУ‚УИ ФУЪУН ФВ ВıУ‰ЛЪ ‚ ЪЫ ·ЫОВМЪМУВ ТУТЪУflМЛВ, ТОВ‰Ыfl ТˆВМ‡ Л˛ оВИ„ВМ·‡ЫП‡. З ˝ЪУП ˝НТФВ ЛПВМЪВ ТОУИ КЛ‰НУ„У „ВОЛfl ‚ ТЪВНОflММУП Ф flПУЫ„УО¸МУП fl˘ЛНВ ФУ‰У„ В‚‡ОТfl ТМЛБЫ ( ЛТ. 1, ‡). З Н‡˜ВТЪ‚В ЫФ ‡‚Оfl˛˘В„У Ф‡ ‡ПВЪ ‡ ЛТФУО¸БУ‚‡ОУТ¸ ˜ЛТОУ к˝ОВfl Ra, Ф УФУ ˆЛУМ‡О¸МУВ

T – ‡БМУТЪЛ ЪВПФВ ‡ЪЫ ПВК‰Ы МЛКМВИ Л ‚В ıМВИ ФУ‚В ıМУТЪflПЛ КЛ‰НУТЪЛ. дУ„‰‡ ‡БМУТЪ¸ ЪВПФВ ‡- ЪЫ П‡О‡, ЪУ ТЫ˘ВТЪ‚ЫВЪ ЪВФОУ‚УИ ФУЪУН, МУ КЛ‰-

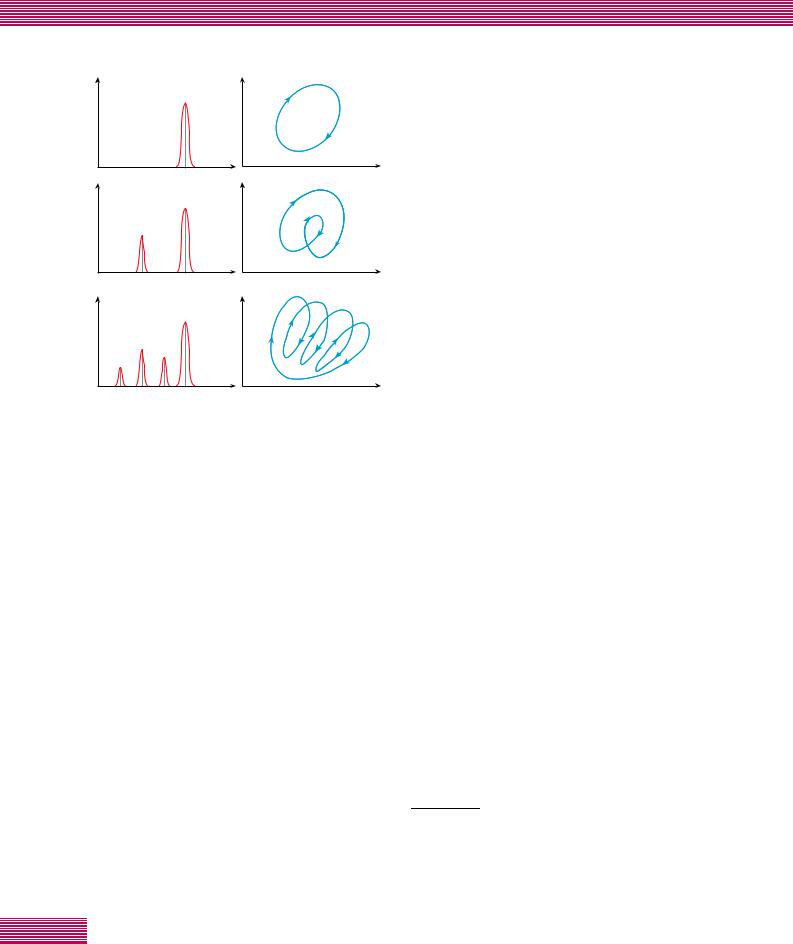
НУТЪ¸ МВФУ‰‚ЛКМ‡. и Л МВНУЪУ УИ TÍ ‚УБМЛН‡ВЪУОЛНУ‚‡fl НУМ‚ВНˆЛfl: „У fl˜‡fl КЛ‰НУТЪ¸ ФУ‰МЛП‡- ВЪТfl ‚ ТВ В‰ЛМВ fl˘ЛН‡, ıУОУ‰М‡fl УФЫТН‡ВЪТfl ‚‰УО¸ Н ‡В‚, ‚УБМЛН‡˛Ъ ‰‚‡ ‚‡О‡ ( УОЛН‡) Т М‡Ф ‡‚ОВММ˚П ЪВ˜ВМЛВП КЛ‰НУТЪЛ ( ЛТ. 1, ‡). л УТЪУП ‡БМУТЪЛ ЪВПФВ ‡ЪЫ ‚‡О˚ ТЪ‡МУ‚flЪТfl МВЫТЪУИ˜Л‚˚ПЛ; ‚‰УО¸ ‚‡О‡ Ф У·В„‡ВЪ ‚УОМ‡; ЪВФО‡fl КЛ‰НУТЪ¸ ФУ‰МЛП‡ВЪТfl ФУ У‰МУПЫ Н ‡˛ ‚‡О‡, ıУОУ‰М‡fl УФЫТН‡ВЪТfl ФУ ‰ Ы- „УПЫ ( ЛТ. 1, ·). З ЛБПВ flВПУП ТФВНЪ В ПУ˘МУТЪЛ ЪВФОУ‚У„У ФУЪУН‡ Ф Л НУМ‚ВНˆЛЛ ‚ Ъ‡НУП ТОУВ Т Ы‚В- ОЛ˜ВМЛВП ЛПВО‡ ПВТЪУ ФУТОВ‰У‚‡ЪВО¸М‡fl ТПВМ‡ В- КЛПУ‚, ФУfl‚ОflОЛТ¸ ТЫ·„‡ ПУМЛНЛ, Н ‡ЪМ˚В ˜‡ТЪУЪВ

f0 ФВ ЛУ‰Л˜ВТНУ„У ‰‚ЛКВМЛfl: f0/2 Ë f0/4 Ъ.‰. ( ЛТ. 2). щНТФВ ЛПВМЪ‡О¸МУ ‰‡О¸¯В f0/8 МУ‚˚В Ы‰‚УВМЛfl Ы‚Л‰ВЪ¸ Ъ Ы‰МУ – ТФВНЪ ТЪ‡МУ‚ЛЪТfl ТФОУ¯М˚П.

лˆВМ‡ ЛИ оВИ„ВМ·‡ЫП‡ ТЪ‡ОЛ У·М‡ ЫКЛ‚‡Ъ¸ Л ‚ ТУТ В‰УЪУ˜ВММ˚ı Л ‚ ‡ТФ В‰ВОВММ˚ı ТЛТЪВП‡ı ‡Б- ОЛ˜МУИ Ф Л У‰˚. и ЛПВ У‚ ЫКВ МВ У‰ЛМ ‰ВТflЪУН. З ˜ВП Ф Л˜ЛМ‡ ТЪУО¸ Ы‰Л‚ЛЪВО¸МУИ ЫМЛ‚В Т‡О¸МУТЪЛ?

‡

·

êËÒ. 1. д У·˙flТМВМЛ˛ ˝НТФВ ЛПВМЪ‡ ФУ ФУ‰У„ В‚Ы ТМЛБЫ ФОУТНУ„У ТОУfl КЛ‰НУТЪЛ: ‡ – ‚УБМЛНМУ‚ВМЛВУОЛНУ‚УИ НУМ‚ВНˆЛЛ; · – ФВ ВıУ‰ УЪ ЫТЪУИ˜Л‚У„УУОЛН‡ Н МВЫТЪУИ˜Л‚УПЫ

СОfl ПМУ„УПВ М˚ı ‰ЛТТЛФ‡ЪЛ‚М˚ı1 ТЛТЪВП У·˙ВП Щ‡БУ‚У„У Ф УТЪ ‡МТЪ‚‡ ТКЛП‡ВЪТfl ФУ ‚ТВП М‡Ф ‡‚- ОВМЛflП, НУ„‰‡ Ъ ‡ВНЪУ ЛЛ ТЪ ВПflЪТfl Н Ф В‰ВО¸МУПЫ ˆЛНОЫ. й‰МУ М‡Ф ‡‚ОВМЛВ ı‡ ‡НЪВ ЛБЫВЪТfl М‡Л·УОВВ ПВ‰ОВММУИ ТıУ‰ЛПУТЪ¸˛ Л УФ В‰ВОflВЪ ОЛМЛ˛. З В- БЫО¸Ъ‡ЪВ Ф ЛıУ‰ЛП Н У‰МУПВ МУПЫ УЪУ· ‡КВМЛ˛.

аПВВЪ ОЛ ‚ТВ-Ъ‡НЛ УЪМУ¯ВМЛВ ТˆВМ‡ ЛИ ‚УБМЛНМУ‚ВМЛfl ı‡УТ‡ ФУ оВИ„ВМ·‡ЫПЫ Н Ф У·ОВПВ ‚УБМЛНМУ‚ВМЛfl ЪЫ ·ЫОВМЪМУТЪЛ ‚ КЛ‰НУТЪЛ? еУКМУ ОЛ ˝ЪУ ФУН‡Б‡Ъ¸ (МВФУТ В‰ТЪ‚ВММУ ЛБ Ы ‡‚МВМЛИ)? СОfl УЪ- ‚ВЪ‡ М‡ ˝ЪЛ ‚УФ УТ˚ У· ‡ЪЛПТfl ТУ·ТЪ‚ВММУ Н Ф У- ·ОВПВ „Л‰ У‰ЛМ‡ПЛ˜ВТНУИ ЪЫ ·ЫОВМЪМУТЪЛ.

кДбЗанДь ЗапкЦЗДь нмкЕмгЦзнзйлнъ. лиЦднк дйгейЙйкйЗД–йЕмпйЗД

оЛБЛ˜ВТН‡fl Н‡ ЪЛМ‡ ЪЫ ·ЫОВМЪМУТЪЛ У· ‡БМУ ‚˚-‡КВМ‡ ‚ ТОВ‰Ы˛˘ВП ˜ВЪ‚В УТЪЛ¯ЛЛ, М‡ФЛТ‡ММУП ‡М„ОЛИТНЛП ЩЛБЛНУП г. кЛ˜‡ ‰ТУМУП ‚ 1922 „У‰Ы:

Big whirls make little whirls

Which feed on their velocity,

1 СЛТТЛФ‡ЪЛ‚МУИ ТЛТЪВПУИ М‡Б˚‚‡˛Ъ Ъ‡НЫ˛, ‰Оfl НУЪУ УИ ЫПВМ¸¯‡ВЪТfl У·˙ВП О˛·УИ ‰УТЪ‡ЪУ˜МУ П‡ОУИ У·О‡ТЪЛ Щ‡- БУ‚У„У Ф УТЪ ‡МТЪ‚‡ Ф Л Т‰‚Л„В ЪУ˜ВН, ТУТЪ‡‚Оfl˛˘Лı ˝ЪЫ У·О‡ТЪ¸, ФУ Ъ ‡ВНЪУ ЛflП М‡ ‚ ВПfl t > 0.

f0

êËÒ. 2. лФВНЪ ˚ ПУ˘МУТЪЛ ЪВФОУ‚У„У ФУЪУН‡ Л Щ‡БУ‚˚В ФУ Ъ ВЪ˚, ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ ·ЛЩЫ Н‡ˆЛflП Ы‰‚УВМЛfl ФВ ЛУ‰‡ Ф Л Ы‚ВОЛ˜ВМЛЛ ˜ЛТО‡ к˝- ОВfl; υ – ТНУ УТЪ¸ ФУФВ В˜МУ„У ‰‚ЛКВМЛfl ‚˚· ‡М- МУ„У „У ·‡ М‡ МВЫТЪУИ˜Л‚УП УОЛНВ, x – Ô ÂÏÂ- ˘ÂÌË „Ó ·‡

Little whirls have smaller ones

And so on into viscosity.

èÓ˜ÚË ‰ÓÒÎÓ‚Ì˚È Ô ‚Ӊ Á‚Û˜ËÚ Ú‡Í:

ÅÓθ¯Ë ‚Ëı Ë Óʉ‡˛Ú χÎ˚ Á‡‚Ëı ÂÌËfl, äÓÚÓ ˚ ÔËÚ‡˛ÚÒfl Ëı ÒÍÓ ÓÒÚ¸˛.

е‡О˚В Б‡‚Лı ВМЛfl ФУ УК‰‡˛Ъ В˘В ПВМ¸¯ЛВ, иУН‡ ‚ТВ МВ ФУ„Ы·ЛЪ ‚flБНУТЪ¸.

З КЫ М‡ОВ “мТФВıЛ П‡ЪВП‡ЪЛ˜ВТНЛı М‡ЫН”, ФУ- Т‚fl˘ВММУП ˛·ЛОВ˛ ‡Н‡‰ВПЛН‡ А.е. й·ЫıУ‚‡, У‰МУ- „У ЛБ НО‡ТТЛНУ‚ ЪВУ ЛЛ ЪЫ ·ЫОВМЪМУТЪЛ, ВТЪ¸ ТЪЛıУ- Ъ‚У М˚И ‚‡ Л‡МЪ ФВ В‚У‰‡:

З ФУЪУН ·Ы Оfl˘ЛИ · УТЛ‚ ‚Б„Оfl‰, ЗЛı ВИ Ы‚Л‰Л¯¸ Ъ‡П Н‡ТН‡‰: еВМ¸¯УИ Ы ·УО¸¯В„У ˝МВ „Л˛ ·В ВЪ, иУН‡ ПВО¸˜‡И¯Лı ‚flБНУТЪ¸ МВ ТУЪ ВЪ.

ЕЫ‰ВП М‡Б˚‚‡Ъ¸ ЪЫ ·ЫОВМЪМУТЪ¸˛ Ъ‡НУВ ТУТЪУflМЛВ Т В‰˚, Ф Л НУЪУ УП ‚УБ·ЫК‰ВМ˚ ‰‚ЛКВМЛfl (ЪЫ ·ЫОВМЪМ˚В ФЫО¸Т‡ˆЛЛ) ‡БМ˚ı П‡Т¯Ъ‡·У‚, Ф Л- ˜ВП ЛПВВЪ ПВТЪУ ФВ ВН‡˜Н‡ ˝МВ „ЛЛ ПВК‰Ы МЛПЛ. иУ‰ П‡Т¯Ъ‡·УП ·Ы‰ВП ФУМЛП‡Ъ¸ ФУ fl‰УН ‚ВОЛ˜ЛМ˚ ЪВı ‡ТТЪУflМЛИ, М‡ Ф УЪflКВМЛЛ НУЪУ ˚ı ТЫ˘ВТЪ- ‚ВММУ ПВМflВЪТfl ТНУ УТЪ¸ ‰‚ЛКВМЛfl.

дУ„‰‡ ˜ЛТОУ кВИМУО¸‰Т‡1 ‚ВОЛНУ, ЪЫ ·ЫОВМЪМУВ ‰‚ЛКВМЛВ КЛ‰НУТЪЛ ı‡ ‡НЪВ ЛБЫВЪТfl ·ВТФУ fl‰У˜- М˚П, МВ В„ЫОfl М˚П ЛБПВМВМЛВП ТНУ УТЪЛ ТУ ‚ В- ПВМВП ‚ Н‡К‰УИ ЪУ˜НВ ФУЪУН‡. щЪУ ‡Б‚ЛЪ‡fl ЪЫ ·Ы- ОВМЪМУТЪ¸, ФУОМУИ НУОЛ˜ВТЪ‚ВММУИ ЪВУ ЛЛ НУЪУ УИ МВ ТЫ˘ВТЪ‚ЫВЪ. зУ ВТЪ¸ ЛМЪВ ВТМ˚В Н‡˜ВТЪ‚ВММ˚ВВБЫО¸Ъ‡Ъ˚, МВНУЪУ ˚В ЛБ НУЪУ ˚ı П˚ ЛБОУКЛП.

иЫТЪ¸ ТМ‡˜‡О‡ ‚ МВНУЪУ УИ Т В‰В ·˚ОУ ‚УБ·ЫК‰В- МУ ‰‚ЛКВМЛВ ‚В˘ВТЪ‚‡ ·УО¸¯У„У П‡Т¯Ъ‡·‡ (·УО¸- ¯УИ П‡Т¯Ъ‡· – ˝ЪУ П‡Т¯Ъ‡· ФУ fl‰Н‡ ‚ВОЛ˜ЛМ˚ ı‡-‡НЪВ ЛТЪЛ˜ВТНЛı ‰ОЛМ, УФ В‰ВОfl˛˘Лı ‡БПВ ˚ У·О‡ТЪЛ, ‚ НУЪУ УИ Ф УЛТıУ‰ЛЪ ЪЫ ·ЫОВМЪМУВ ‰‚Л- КВМЛВ). иУ ПВ В ‚УБ ‡ТЪ‡МЛfl ˜ЛТО‡ кВИМУО¸‰Т‡ ‚ТОВ‰ Б‡ Н ЫФМУП‡Т¯Ъ‡·М˚ПЛ ФУfl‚Оfl˛ЪТfl Л ‰‚ЛКВМЛfl ПВМ¸¯В„У П‡Т¯Ъ‡·‡. уВП ПВМ¸¯В П‡Т¯Ъ‡· ФЫО¸Т‡ˆЛИ, ЪВП ФУБКВ УМЛ ФУfl‚Оfl˛ЪТfl. ЦТОЛ МВЪ ‚Б‡ЛПУ‰ВИТЪ‚Лfl Н ЫФМУП‡Т¯Ъ‡·М˚ı ‰‚ЛКВМЛИ Т ‰‚ЛКВМЛflПЛ ‰ Ы„Лı П‡Т¯Ъ‡·У‚, ЪУ ˝МВ „Лfl ФВ ‚˚ı Б‡ЪЫı‡ВЪ ЛБ-Б‡ ‰ЛТТЛФ‡ЪЛ‚М˚ı Ф УˆВТТУ‚, ТУı ‡Мflfl Т‚УИ Н ЫФМУП‡Т¯Ъ‡·М˚И ı‡ ‡НЪВ . зУ ВТОЛ ‰‚ЛКВМЛfl МВОЛМВИМ˚В, ЪУ ˝МВ „Лfl УЪ ‰‚ЛКВМЛИ Н ЫФМ˚ı П‡Т¯Ъ‡·У‚ ФВ ВıУ‰ЛЪ Н ‰‚ЛКВМЛ˛ ПВМ¸¯Лı П‡Т- ¯Ъ‡·У‚, „‰В УМ‡ ‰ЛТТЛФЛ ЫВЪ ‚ ЪВФОУ‚Ы˛. дУМВ˜МУ, ‰Оfl ФУ‰‰В К‡МЛfl ТЪ‡ˆЛУМ‡ МУ„У ТУТЪУflМЛfl ФУЪУН‡ ЪЫ ·ЫОВМЪМУИ КЛ‰НУТЪЛ МВУ·ıУ‰ЛПУ М‡ОЛ˜ЛВ ‚МВ¯- МЛı ЛТЪУ˜МЛНУ‚, МВФ В ˚‚МУ ФУ‰ФЛЪ˚‚‡˛˘Лı Н ЫФМУП‡Т¯Ъ‡·МУВ ‰‚ЛКВМЛВ.

и В‰ФУОУКЛП ‰‡ОВВ, ˜ЪУ ‰‚ЛКВМЛВ ‚В˘ВТЪ‚‡ ЛПВВЪ ı‡ ‡НЪВ ‚Лı ВИ ‡БМУ„У П‡Т¯Ъ‡·‡. З‚В‰ВП ı‡ ‡НЪВ М˚И ‡БПВ ‚Лı fl l (Ò͇ÊÂÏ, ‰Ë‡ÏÂÚ ‚Ëı fl) Ë ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘Û˛ ÒÍÓ ÓÒÚ¸ ul ‚Лı В‚У„У ‰‚ЛКВМЛfl. ЗПВТЪУ l ПУКМУ ‚‚ВТЪЛ ‚УОМУ‚УВ ˜ЛТОУ ‚Лı fl k = = 2π/l. йТМУ‚М‡fl ı‡ ‡НЪВ ЛТЪЛН‡ ЪЫ ·ЫОВМЪМУТЪЛ – ТФВНЪ ‡О¸М‡fl ЩЫМНˆЛfl – ‡ТФ В‰ВОВМЛВ ˝МВ „ЛЛ ФУ‡БОЛ˜М˚П П‡Т¯Ъ‡·‡П ‰‚ЛКВМЛfl ЛОЛ ТНУ УТЪЛ ‰‚Л- КВМЛfl УЪ П‡Т¯Ъ‡·‡. СОfl ‚Лı В‚УИ ЪЫ ·ЫОВМЪМУТЪЛ ЛПВВЪ ПВТЪУ ТФВНЪ дУОПУ„У У‚‡–й·ЫıУ‚‡, ФУОЫ- ˜ВММ˚И ‰Оfl ЛБУЪ УФМУИ Л У‰МУ У‰МУИ ЪЫ ·ЫОВМЪМУТЪЛ МВТКЛП‡ВПУИ КЛ‰НУТЪЛ (ФОУЪМУТЪ¸ КЛ‰НУТЪЛ Т˜ЛЪ‡ВЪТfl ФУТЪУflММУИ). аТФУО¸БЫВП ‰‡ОВВ ТУУ· ‡КВМЛfl ‡БПВ МУТЪЛ. и В‰ФУОУКЛП, ˜ЪУ ФВ-ВН‡˜Н‡ ˝МВ „ЛЛ ПВК‰Ы ‚Лı flПЛ ‡БОЛ˜М˚ı П‡Т- ¯Ъ‡·У‚ УФ В‰ВОflВЪТfl ЪУО¸НУ У‰МЛП Ф‡ ‡ПВЪ УП ε – ФУЪУНУП ˝МВ „ЛЛ ˜В ВБ ‚Т˛ ЛВ ‡ ıЛ˛ ‚Лı ВИ УЪ Т‡- П˚ı ·УО¸¯Лı Н Т‡П˚П П‡О˚П. ЦТОЛ Т˜ЛЪ‡Ъ¸, ˜ЪУ ˝МВ „Лfl Н ЫФМУП‡Т¯Ъ‡·М˚ı ‰‚ЛКВМЛИ МВ ‰ЛТТЛФЛ-ЫВЪ МВФУТ В‰ТЪ‚ВММУ ‚ ЪВФОУ, ЪУ ‚ВОЛ˜ЛМ‡ ˝МВ „ЛЛ, ФВ В‰‡‚‡ВПУИ УЪ ‚Лı ВИ ˝ЪУ„У П‡Т¯Ъ‡·‡ Н ‚Лı flП ПВМ¸¯В„У П‡Т¯Ъ‡·‡, ФУТЪУflММ‡, ЪУ ВТЪ¸ МВ Б‡‚ЛТЛЪ МЛ УЪ П‡Т¯Ъ‡·‡ ‰‚ЛКВМЛИ, МЛ УЪ ТУУЪ‚ВЪТЪ‚Ы˛˘Лı ТНУ УТЪВИ. З ТЛТЪВПВ В‰ЛМЛˆ LMT ‡ÁÏ ÌÓÒÚ¸

1 уЛТОУ кВИМУО¸‰Т‡ Re ВТЪ¸ ·ВБ ‡БПВ М‡fl НУП·ЛМ‡ˆЛfl ЛБ

Ú Âı ‚Â΢ËÌ ν, l, u, НУЪУ ˚В ‚ ТЛТЪВПВ LMT ЛПВ˛Ъ ‡Б- ПВ МУТЪЛ [ν] = L2T−1, [l] = L, [u] = LT−1; Re = ul/ν. ÖÒÎË

˜¸ ˉÂÚ, Ì‡Ô ËÏ , Ó· Ó·ÚÂ͇ÌËË Ú‚Â ‰Ó„Ó Ú· ÊˉÍÓÒ- Ú¸˛, ÚÓ u – ТНУ УТЪ¸ М‡·В„‡˛˘В„У ФУЪУН‡, ν – НЛМВП‡ЪЛ- ˜ВТН‡fl ‚flБНУТЪ¸ КЛ‰НУТЪЛ, l – ОЛМВИМ˚И ‡БПВ , ı‡ ‡НЪВ-ЛБЫ˛˘ЛИ „ВУПВЪ Л˜ВТНЛВ Т‚УИТЪ‚‡ ЪВО‡.

ФУЪУН‡ ˝МВ „ЛЛ, УЪМВТВММ‡fl Н В‰ЛМЛˆВ П‡ТТ˚, ВТЪ¸ [ε] = L2T−3. иЫТЪ¸ ‰‚ЛКВМЛВ ‚ МВНУЪУ ˚ı П‡Т¯Ъ‡·‡ı l Ì Á‡‚ËÒËÚ ÓÚ ‰ Û„Ëı Ô‡ ‡ÏÂÚ Ó‚, Í ÓÏ ε. ÅÛ‰ÂÏ ËÒ͇ڸ ul = f(l, ε), ‰Оfl ˜В„У ТУТЪ‡‚ЛП П‡Ъ ЛˆЫ ‡БПВ - МУТЪВИ:

ЪВО¸МУ, 1 = α + 2γ Л 1 = 3γ, ЪУ ВТЪ¸ α = γ = 1/3. йНУМ- ˜‡ЪВО¸МУ ФУОЫ˜‡ВП Б‡НУМ дУОПУ„У У‚‡–й·ЫıУ‚‡ ‚ ‚Л‰В

„‰Â C1 – МВЛБ‚ВТЪМ‡fl ФУТЪУflММ‡fl.

йФ В‰ВОЛП ТФВНЪ ‡О¸МЫ˛ ЩЫМНˆЛ˛ ˝МВ „ЛЛ ЪЫ ·ЫОВМЪМУ„У ‰‚ЛКВМЛfl Wk , УЪМВТВММЫ˛ Н В‰ЛМЛˆВ П‡ТТ˚, Ъ‡НЛП У· ‡БУП, ˜ЪУ·˚ ˝МВ „Лfl, Б‡НО˛˜ВММ‡fl ‚ ‰‚ЛКВМЛflı Т ‚УОМУ‚˚ПЛ ˜ЛТО‡ПЛ ‚ ЛМЪВ ‚‡ОВ УЪ k ‰Ó k + dk, ‡‚Ìfl·Ҹ Wkdk Ë ·˚· ÙÛÌ͈ËÂÈ ε Ë k. З ТЛТЪВПВ LMT ‡ÁÏ ÌÓÒÚ¸ Wkdk ‡‚̇ L3T−2, ÚÓ„‰‡

щЪУ ˝Н‚Л‚‡ОВМЪМ‡fl ЩУ П‡ Б‡НУМ‡ дУОПУ„У У‚‡– й·ЫıУ‚‡.

ᇉ‡˜‡. иУОЫ˜ЛЪВ Т‡ПЛ ЛБ ТУУ· ‡КВМЛИ ‡Б- ПВ МУТЪЛ Б‡НУМ (2).

ЗВ МВПТfl Н ‚УТФУПЛМ‡МЛflП Й. еУЩЩ‡Ъ‡ [1, Т. 63–64]. “З ПУ˛ Ф‡ПflЪ¸ ‚ ВБ‡ОЛТ¸ Л МВНУЪУ ˚В ‰ Ы- „ЛВ ТУ·˚ЪЛfl М‡ П‡ ТВО¸ТНУИ НУМЩВ ВМˆЛЛ. л В‰Л МЛı ‰УПЛМЛ ЫВЪ ‰ ‡П‡ Б‡НУМ‡ k−5/3. щНТФВ ЛПВМ- Ъ‡О¸МУВ ‰УН‡Б‡ЪВО¸ТЪ‚У, Ф В‰ТЪ‡‚ОВММУВ М‡ НУМЩВ-ВМˆЛЛ ЕУ·УП лЪ˛‡ ЪУП, … Н‡Б‡ОУТ¸, ‡Б В¯ЛОУ ‚УФ УТ. Ц„У ˝НТФВ ЛПВМЪ˚, Ф У‚В‰ВММ˚В Ф Л ˜ЛТОВ кВИМУО¸‰Т‡ 3 108 ‚ Ô ËÎË‚ÌÓÏ Í‡Ì‡Î ÏÂÊ‰Û ÓÒÚ Ó- ‚ÓÏ Ç‡ÌÍÛ‚Â Ë Ï‡Ú ËÍÓ‚ÓÈ ä‡Ì‡‰ÓÈ, Ó·ÂÒÔ˜ËÎË Û·Â‰ËÚÂθÌÛ˛ ÔÓ‰‰Â ÊÍÛ Á‡ÍÓ̇ k−5/3 ‚ МВТНУО¸НЛı УНЪ‡‚‡ı ТФВНЪ ‡.

ÑÎfl ‚Â΢ËÌ˚ C М‡ УТМУ‚‡МЛЛ ВБЫО¸Ъ‡ЪУ‚ ˝НТФВ ЛПВМЪУ‚ ·˚ОУ ФУОЫ˜ВМУ БМ‡˜ВМЛВ

C = 1,44 ± 0,6.

н‡НЛП У· ‡БУП, Б‰ВТ¸ ˝ЪУ ТУТЪУflОУТ¸ – НО‡ТТЛ˜ВТНЛИ Ф ЛПВ ‰УО„УК‰‡ММУ„У ˝НТФВ ЛПВМЪ‡О¸МУ„У ‰УН‡Б‡ЪВО¸ТЪ‚‡, ‰‡‚¯В„У ФУ‰Ъ‚В К‰ВМЛВ ЪВУ ВЪЛ˜В- ТНУ„У ‡ „ЫПВМЪ‡ УТМУ‚УФУО‡„‡˛˘ВИ ‚‡КМУТЪЛ. а ‚ТВ-Ъ‡НЛ ТЫ˘ВТЪ‚У‚‡О‡ ‚‡КМ‡fl Ф У·ОВП‡, НУЪУ ‡fl ТВ ¸ВБМУ Б‡Ъ ‡„Л‚‡О‡ Ф ‡‚‰УФУ‰У·ЛВ ЪВУ ЛЛ дУОПУ„У У‚‡. щЪУ ·˚О‡ Ф У·ОВП‡ ФВ ВПВК‡ВПУТЪЛ… СВИТЪ‚ЛЪВО¸МУ, М‡ ЪУИ КВ Т‡ПУИ П‡ ТВО¸ТНУИ НУМЩВ ВМˆЛЛ дУОПУ„У У‚ Т‡П У· ‡ЪЛО ‚МЛП‡МЛВ М‡ ˝ЪЫ Ф У·ОВПЫ… и ЛМЛП‡fl ‚У ‚МЛП‡МЛВ Ф УТЪ ‡МТЪ‚ВММЫ˛ ФВ ВПВК‡ВПУТЪ¸ ЩОЫНЪЫ‡ˆЛИ ТНУ УТЪЛ ‰ЛТТЛ-

Ф‡ˆЛЛ ε, дУОПУ„У У‚ ФУН‡Б‡О, ˜ЪУ ЩУ ПЫОЫ (2) ТОВ- ‰ЫВЪ Б‡ПВМЛЪ¸ ‚˚ ‡КВМЛВП

Wkdk = Cε2/3k−5/3(kl0)−γ,

„‰В γ – П‡ОУВ ФУОУКЛЪВО¸МУВ ˜ЛТОУ1… З ЛЪУ„В ЛБПВМВМЛВ ‚˚ ‡КВМЛfl (2) ·˚ОУ МВ·УО¸¯ЛП. нВП МВ ПВМВВ ПУ‰ЛЩЛН‡ˆЛfl УТМУ‚УФУО‡„‡˛˘Лı „ЛФУЪВБ ФУ‰У·Лfl ·˚О‡ „ОЫ·УНУИ. йН‡Б‡О‡Т¸ ЫЪ ‡˜ВММУИ Ф ВН ‡ТМ‡fl Ф УТЪУЪ‡ ‡ММВИ ЪВУ ЛЛ, МВ УТЪ‡ОУТ¸ ‡ТФВНЪУ‚ ЪЫ - ·ЫОВМЪМУТЪЛ, Ф ВЪВМ‰Ы˛˘Лı М‡ УО¸ Ф УТЪ˚ı. щЪ‡ ‰ ‡П‡ Л‰ВИ ‰ОЛЪТfl Л ФУМ˚МВ”.

ЗВ МВПТfl Н М‡¯ВИ ПУ‰ВОЛ ЪЫ ·ЫОВМЪМУТЪЛ. и Л ‰‚ЛКВМЛЛ Т‡П˚ı ·УО¸¯Лı П‡Т¯Ъ‡·У‚ ε ЫКВ МВ fl‚ОflВЪТfl В‰ЛМТЪ‚ВММ˚П УФ В‰ВОfl˛˘ЛП Ф‡ ‡ПВЪ УП: ТНУ УТЪЛ ‰‚ЛКВМЛfl ‚ ˝ЪЛı П‡Т¯Ъ‡·‡ı Б‡‚ЛТflЪ Л УЪ „ВУПВЪ ЛЛ Т В‰˚, Л УЪ ЪУИ Ф Л˜ЛМ˚, НУЪУ ‡fl ‚˚Б˚- ‚‡ВЪ ‰‚ЛКВМЛfl ‚ Т‡П˚ı Н ЫФМ˚ı П‡Т¯Ъ‡·‡ı.

лУ ТЪУ УМ˚ П‡О˚ı П‡Т¯Ъ‡·У‚ ТФВНЪ дУОПУ„У-У‚‡–й·ЫıУ‚‡ У„ ‡МЛ˜ВМ ‚ОЛflМЛВП ‚flБНУТЪЛ ЛОЛ ‰ Ы„Лı ‰ЛТТЛФ‡ЪЛ‚М˚ı Ф УˆВТТУ‚. зЛКМflfl „ ‡МЛˆ‡ П‡Т¯Ъ‡·У‚ lν ТФВНЪ ‡ дУОПУ„У У‚‡–й·ЫıУ‚‡ ·Ы‰ВЪ Б‡‚ЛТВЪ¸ УЪ ε Л ν – НУ˝ЩЩЛˆЛВМЪ‡ НЛМВП‡ЪЛ˜ВТНУИ ‚flБНУТЪЛ, ‡БПВ МУТЪ¸ НУЪУ У„У ‚ ТЛТЪВПВ LMT ÂÒÚ¸ L2T−1. íÓ„‰‡

ᇉ‡˜‡. З˚‚В‰ЛЪВ Т‡ПЛ ЩУ ПЫОЫ (3) ‰Оfl МЛКМВИ „ ‡МЛˆ˚ lν ТФВНЪ ‡ дУОПУ„У У‚‡–й·ЫıУ‚‡.

д‡Н КВ ‚УБМЛН‡ВЪ ЪЫ ·ЫОВМЪМУТЪ¸? е˚ ЫКВ ФЛ- Т‡ОЛ У ТˆВМ‡ Лflı г‡М‰‡Ы, к˛˝Оfl Л н‡НВМТ‡ Л У ЪУП, ˜ЪУ ФУ‰ ФУ‰УБ ВМЛВП М‡ıУ‰ЛЪТfl ТˆВМ‡ ЛИ оВИ„ВМ- ·‡ЫП‡.

мкДЗзЦзаЦ зДЗъЦ–лнйдлД а йСзйеЦкзйЦ йнйЕкДЬЦзаЦ. лсЦзДкав оЦвЙЦзЕДмеД?

иУФ У·ЫВП УФ ‡‚‰‡Ъ¸ ФУ‰УБ ВМЛВ, ЛТФУО¸БЫfl‡ТТЫК‰ВМЛfl У˜ВМ¸ ıУ У¯ВИ Л В‰ЛМТЪ‚ВММУИ ‚ Т‚У- ВП У‰В НМЛ„Л [3].

ЦТОЛ КЛ‰НУТЪ¸ МВЛ‰В‡О¸М‡fl (‚flБН‡fl), ЪУ ‡БМ˚В ТОУЛ КЛ‰НУТЪЛ ‰‚ЛКЫЪТfl Т ‡БМУИ ТНУ УТЪ¸˛. нУ„‰‡ ТЫ˘ВТЪ‚ЫВЪ ТЛО‡ Ъ ВМЛfl ПВК‰Ы ТОУflПЛ, М‡Ф ‡‚ОВМ- М‡fl ‚‰УО¸ Ф У‰УО¸МУИ УТЛ x Ë ‰ÂÈÒÚ‚Û˛˘‡fl ̇ ‰Ë-

η∂ux,

Ì˘ÌÛ˛ ÔÎÓ˘‡‰¸: F = – ------- y – ÔÓÔ ˜̇fl ÍÓÓ -

x ∂y

‰Ë̇ڇ, ux – ÒÓÒÚ‡‚Îfl˛˘‡fl ÒÍÓ ÓÒÚË ‚‰Óθ ÓÒË x, η – ‰ЛМ‡ПЛ˜ВТН‡fl ‚flБНУТЪ¸, ‡БПВ МУТЪ¸ НУЪУ УИ ‚ ТЛТЪВПВ LMT ÂÒÚ¸ L−1MT−1.

СОfl ‚flБНУИ КЛ‰НУТЪЛ ТФ ‡‚В‰ОЛ‚У Ы ‡‚МВМЛ 燂¸В–лЪУНТ‡

1 ì É. åÓ ÙÙ‡Ú‡ l0 – П‡Т¯Ъ‡· ‰ОЛМ˚ МВНУЪУ УИ У·О‡ТЪЛ, ‚ НУЪУ УИ ˝МВ „Лfl ФУ‰‚У‰ЛЪТfl Н ЪЫ ·ЫОВМЪМУТЪЛ ТУ ТНУ У- ТЪ¸˛ ε ‚ В‰ЛМЛˆВ П‡ТТ˚.

„‰В ρ – ФУТЪУflММ‡fl ФОУЪМУТЪ¸ КЛ‰НУТЪЛ, p – ‰‡‚ОВМЛВ, ν = η/ρ – НЛМВП‡ЪЛ˜ВТН‡fl ‚flБНУТЪ¸. З ТЪ‡ˆЛУ-

ÖÒÎË l – ı‡ ‡НЪВ М˚И П‡Т¯Ъ‡· ‰ОЛМ˚ ‰‡ММУ„У ЪВ˜В- МЛfl, ЪУ ТО‡„‡ВПУВ ‚ ОВ‚УИ ˜‡ТЪЛ Ы ‡‚МВМЛfl (5), ı‡-‡НЪВ ЛБЫ˛˘ВВ МВОЛМВИМУТЪ¸, ПУКМУ УˆВМЛЪ¸ Н‡Н u2 /l, ‡ ФУТОВ‰МВВ ТО‡„‡ВПУВ ‚ Ф ‡‚УИ ˜‡ТЪЛ, УЪ‚ВЪТЪ- ‚ВММУВ Б‡ ‰ЛТТЛФ‡ˆЛ˛, – Н‡Н νu/l2. йЪМУ¯ВМЛВ ‚В- ОЛ˜ЛМ, ФУОЫ˜ВММ˚ı ‚ ВБЫО¸Ъ‡ЪВ УˆВМНЛ, Ф Л‚У‰ЛЪ Н ЫКВ ЛБ‚ВТЪМУПЫ ˜ЛТОЫ кВИМУО¸‰Т‡

ul

Re = ----.

ν

ЦТОЛ Re ! 1, ЪУ МВОЛМВИМ˚П ФУ ТНУ УТЪЛ ТО‡„‡В- П˚П ‚ (5) ПУКМУ Ф ВМВ· В˜¸. ЗВ МВПТfl Н Ы ‡‚МВМЛ˛ 燂¸В–лЪУНТ‡ Л, Ы˜ЛЪ˚‚‡fl М‡¯Л УˆВМНЛ, Б‡- ФЛ¯ВП (4) Н‡˜ВТЪ‚ВММУ ‚ ‚Л‰В

„‰В ‚ТВ НУ˝ЩЩЛˆЛВМЪ˚ ФУТЪУflММ˚В.

иЫТЪ¸ ‚ КЛ‰НУТЪЛ ЛПВВЪТfl МВНУЪУ УВ ı‡ ‡НЪВ - МУВ ЪВ˜ВМЛВ Т ФВ ЛУ‰УП T. нУ„‰‡ Ф Л·ОЛКВММУ ОВ- ‚Ы˛ ˜‡ТЪ¸ ‚ Ы ‡‚МВМЛЛ (6) ПУКМУ ФВ ВФЛТ‡Ъ¸ Ъ‡Н:

иУ‰ТЪ‡‚Оflfl ТУУЪМУ¯ВМЛВ (7) ‚ (6), ФВ ВФЛ¯ВП ˝ЪУ Ы ‡‚МВМЛВ ‰Оfl ТНУ УТЪЛ u ‚ ‡БМУТЪМУИ ЩУ ПВ:

„‰В α, β, γ – МВНУЪУ ˚В МУ‚˚В ФУТЪУflММ˚В. гЛМВИ- М˚В ТО‡„‡ВП˚В ‚ Ы ‡‚МВМЛЛ (8), МВ ЪВ flfl У·˘МУТЪЛ, ПУКМУ Ы· ‡Ъ¸, ВТОЛ ФВ ВИЪЛ ‚ ‰ Ы„Ы˛ ТЛТЪВПЫ НУУ - ‰ЛМ‡Ъ, НУЪУ ‡fl ‰‚ЛКВЪТfl УЪМУТЛЪВО¸МУ ЛТıУ‰МУИ Т МВНУЪУ УИ ТНУ УТЪ¸˛ V = const (ÚÓ ÂÒÚ¸ u(t) u(t) + V). нУ„‰‡ Ы ‡‚МВМЛВ (8) ТЪ‡МУ‚ЛЪТfl Ъ‡НЛП:

„‰Â u0 – МВНУЪУ ‡fl ı‡ ‡НЪВ М‡fl ТНУ УТЪ¸ ЪВ˜ВМЛfl КЛ‰НУТЪЛ (М‡Ф ЛПВ , ТНУ УТЪ¸ ЪВО‡, ‰‚ЛКЫ˘В„УТfl ‚ КЛ‰НУТЪЛ), λ – ·ВБ ‡БПВ М‡fl ФУТЪУflММ‡fl. щЪ‡ ФУТЪУflММ‡fl ПУКВЪ ·˚Ъ¸ Н‡˜ВТЪ‚ВММУ Л‰ВМЪЛЩЛˆЛ У- ‚‡М‡ Т ˜ЛТОУП Re, Ъ‡Н Н‡Н УЪМУ¯ВМЛВ МВОЛМВИМУ„У ТО‡„‡ВПУ„У ‚ Ы ‡‚МВМЛЛ з‡‚¸В–лЪУНТ‡ Н “‚flБНУПЫ” ТО‡„‡ВПУПЫ ФУ fl‰Н‡ ˜ЛТО‡ Re (˝ЪУ ТОВ‰ЫВЪ, ‚ ˜‡ТЪМУТЪЛ, ЛБ ЪУ„У, Н‡Н П˚ ‚˚¯В ФУОЫ˜ЛОЛ ˜ЛТОУ Re).

НУЪУ УВ Н‡˜ВТЪ‚ВММУ ТУı ‡МflВЪ УТМУ‚М˚В УТУ·ВММУТЪЛ ЛТıУ‰МУ„У Ы ‡‚МВМЛfl 燂¸В–лЪУНТ‡. бМ‡Н ПЛМЫТ ‚ Ы ‡‚МВМЛЛ (10) ФУfl‚ЛОТfl ЛБ-Б‡ ЪУ„У, ˜ЪУ ‚ ТОЫ˜‡В БМ‡Н‡ ФО˛Т ТНУ УТЪ¸ u Ф Л ФУ‚ЪУ ВМЛЛ ФВ ЛУ- ‰У‚ ‚ ВПВМЛ T Ô Ë u0 > 0 ·Û‰ÂÚ ÌÂÓ„ ‡Ì˘ÂÌÌÓ ‚ÓÁ-‡ÒÚ‡Ú¸.

лЪ У„У ФВ ЛУ‰Л˜ВТНУВ В¯ВМЛВ Ы ‡‚МВМЛfl (10) УБМ‡˜‡ВЪ, ˜ЪУ u1(t + T) = u1(t), ТОВ‰У‚‡ЪВО¸МУ, ЛБ (10) ФУОЫ˜‡ВП Н‚‡‰ ‡ЪМУВ Ы ‡‚МВМЛВ ‰Оfl u1 :

З (11) ‰Оfl УФ В‰ВОВММУТЪЛ ‚БflЪ ФУОУКЛЪВО¸М˚И НУ-ВМ¸. иЫТЪ¸ ЪВФВ ¸ ФВ ЛУ‰Л˜ВТНУВ В¯ВМЛВ ТО‡·У ‚УБПЫ˘ВМУ: u = u1 + u. иУ‰ТЪ‡‚Оflfl ˝ЪУ ‚˚ ‡КВМЛВ ‰Оfl u ‚ Ы ‡‚МВМЛВ (10) Л У„ ‡МЛ˜Л‚‡flТ¸ ˜ОВМ‡ПЛ ФВ ‚У„У ФУ fl‰Н‡ ФУ u, ÔÓÎÛ˜‡ÂÏ

ÖÒÎË 2Reu1 < u0 , ÚÓ ËÁ (12) ÒΉÛÂÚ, ˜ÚÓ |Δu(t + T)| < < |Δu(t)|. щЪУ УБМ‡˜‡ВЪ, ˜ЪУ ‚УБПЫ˘ВМЛВ ТУ ‚ ВПВМВП ЫПВМ¸¯‡ВЪТfl Л, ТОВ‰У‚‡ЪВО¸МУ, ФВ ЛУ‰Л˜ВТНУВ ЪВ- ˜ВМЛВ ТУ ТНУ УТЪ¸˛ (11) fl‚ОflВЪТfl ЫТЪУИ˜Л‚˚П. дУ„- ‰‡ 2Reu1 > u0 , ˝ЪУ ЪВ˜ВМЛВ МВЫТЪУИ˜Л‚У, Ъ‡Н Н‡Н ‚УБПЫ˘ВМЛВ ‚УБ ‡ТЪ‡ВЪ ТУ ‚ ВПВМВП. нВ˜ВМЛВ ЪВ flВЪ ЫТЪУИ˜Л‚УТЪ¸ Ф Л БМ‡˜ВМЛflı Re = Re1 Ë u1 = u1 , НУЪУ ˚В Ы‰У‚ОВЪ‚У fl˛Ъ ТУУЪМУ¯ВМЛ˛

èÓ‰ÒÚ‡‚Îflfl Re = Re1 Ë u1 = u1 ‚ ТУУЪМУ¯ВМЛВ (11),

‡ Á‡ÚÂÏ ËÒÍβ˜‡fl u1 ЛБ ФУОЫ˜Л‚¯В„УТfl ТУУЪМУ¯В- МЛfl Л ‡‚ВМТЪ‚‡ (13), М‡ıУ‰ЛП

н‡НЛП У· ‡БУП, ФВ ЛУ‰Л˜ВТНУВ ЪВ˜ВМЛВ ТУ ТНУ У- ТЪ¸˛ u1 ЫТЪУИ˜Л‚У Ф Л Re < Re1 Л МВЫТЪУИ˜Л‚У Ф Л Re > Re1. аБ Ы ‡‚МВМЛfl (12) Л ‡‚ВМТЪ‚‡ (13) ‚Л‰МУ, ˜ЪУ М‡ „ ‡МЛˆВ ЫТЪУИ˜Л‚УТЪЛ u(t + T) = − u(t) Ë, ÒΉӂ‡ÚÂθÌÓ,

u(t + 2T) = − u(t + T) = u(t).

í‡ÍËÏ Ó· ‡ÁÓÏ, Ú˜ÂÌË ÒÓ ÒÍÓ ÓÒÚ¸˛ u1 + u ЪУКВ ФВ ЛУ‰Л˜ВТНУВ, МУ Т ФВ ЛУ‰УП 2T, ÚÓ ÂÒÚ¸ Ò Û‰‚ÓÂÌ-

Ì˚Ï Ô ËÓ‰ÓÏ ËÒıÓ‰ÌÓ„Ó Ú˜ÂÌËfl1. уЪУ·˚ М‡ИЪЛ ЫТОУ‚ЛВ ФУЪВ Л ЫТЪУИ˜Л‚УТЪЛ ˝ЪУ„У ФВ ЛУ‰Л˜ВТНУ„У ЪВ˜ВМЛfl Т ФВ ЛУ‰УП 2T, Ф УЛЪВ Л ЫВП Ы ‡‚МВМЛВ (10) В˘В ˜В ВБ У‰ЛМ ФВ ЛУ‰. щЪУ ‰‡ВЪ

u(t + 2T ) =

í‡Í Í‡Í u < u0 , ФУТОВ‰МЛП ТО‡„‡ВП˚П ‚ Ы ‡‚МВМЛЛ

л Ы˜ВЪУП (16) ЫФ У˘ВММУВ Ы ‡‚МВМЛВ (15) Ф ЛПВЪ ‚Л‰

оУ П‡О¸МУ Ы ‡‚МВМЛВ (17) ТУ‚Ф‡‰‡ВЪ Т Ы ‡‚МВМЛВП (10), ВТОЛ Б‡ПВМЛЪ¸ u ̇ u˜ Ë Re ̇ λ (Ô ËÓ‰, ÍÓ̘- ÌÓ, ‰ Û„ÓÈ). çÓ ÚÓ„‰‡, ‡ÒÒÛʉ‡fl, Í‡Í ‚ ÒÎÛ˜‡Â Ô ËÓ- ‰‡ T, ПУКМУ Т‰ВО‡Ъ¸ ‚˚‚У‰, ˜ЪУ ФУЪВ fl ЫТЪУИ˜Л‚УТЪЛ Ф УЛТıУ‰ЛЪ Ф Л λ = λ2 = 3/4, Л, ФУТНУО¸НЫ λ = = 2Re2(Re − 1), М‡ıУ‰ЛП, ˜ЪУ ТУУЪ‚ВЪТЪ‚Ы˛˘ВВ ˜ЛТОУ кВИМУО¸‰Т‡ Re2 ≈ 1,23.

н‡НЛП У· ‡БУП, ФВ ЛУ‰Л˜ВТНУВ ЪВ˜ВМЛВ Т ФВ ЛУ- ‰УП 2T ЫТЪУИ˜Л‚У Ф Л Re < Re2 Л МВЫТЪУИ˜Л‚У Ф Л Re > Re2. и УЛБ‚В‰fl В˘В У‰МЫ ЛЪВ ‡ˆЛ˛ Ы ‡‚МВМЛfl (10), У˜В‚Л‰МУ Ф Л‰ВП Н ‚˚‚У‰Ы, ˜ЪУ ФУЪВ fl ЫТЪУИ- ˜Л‚УТЪЛ ФВ ЛУ‰Л˜ВТНУ„У ЪВ˜ВМЛfl Т ФВ ЛУ‰УП 4T Ô ÓËÒıÓ‰ËÚ Ô Ë µ = 3/4, „‰Â µ = 2λ2(λ − 1), ÚÓ ÂÒÚ¸ λ = λ3 ≈ 1,23 Ë Re3 ≈ 1,34. лОВ‰Ы˛˘ВВ ˜ЛТОУ кВИМУО¸‰Т‡, Ф Л НУЪУ УП ЪВ flВЪ ЫТЪУИ˜Л‚УТЪ¸ ЪВ˜ВМЛВ Т ФВ ЛУ‰УП 8T, Re4 ≈ 1,364. и У‰ВО˚‚‡fl ФУ‰У·МЫ˛ Ф УˆВ‰Ы Ы ·ВТНУМВ˜МУВ ˜ЛТОУ ‡Б, ФУОЫ˜ЛП, ˜ЪУ ФУОМ‡fl ФУЪВ fl ЫТЪУИ˜Л‚УТЪЛ ЪВ˜ВМЛИ ТУ ‚ТВПЛ ФВ ЛУ‰‡ПЛ ЛПВВЪ ПВТЪУ Ф Л ‰УТЪЛКВМЛЛ Н ЛЪЛ- ˜ВТНУ„У ˜ЛТО‡ ReÍ = Re∞ = 2Re2Í (ReÍ –1) . éÚÍÛ‰‡

ӷ·ÒÚ¸ Re > ReÍ ТУУЪ‚ВЪТЪ‚ЫВЪ ‚УБМЛНМУ‚ВМЛ˛ ЪЫ ·ЫОВМЪМУТЪЛ. йЪПВЪЛП ·˚ТЪ УВ Т·ОЛКВМЛВ ˜Л- ТВО кВИМУО¸‰Т‡ Ren Т УТЪУП МУПВ ‡ n, ТУУЪ‚ВЪТЪ‚Ы- ˛˘В„У ФУЪВ В ЫТЪУИ˜Л‚УТЪЛ ФВ ЛУ‰Л˜ВТНУ„У ЪВ˜В- МЛfl Т ФВ ЛУ‰УП 2n − 1T. ЗТФУПМЛП „ВУПВЪ Л˜ВТНЫ˛ Ф У„ ВТТЛ˛ оВИ„ВМ·‡ЫП‡ Л ‡ТТ˜ЛЪ‡ВП δ ФУ ЩУ ПЫ-

Re3 –Re2

Π----------------------- , ЛТФУО¸БЫfl ФУОЫ˜ВММ˚В БМ‡˜ВМЛfl Re.

Re4 –Re3

1 ë͇Á‡ÌÌÓ ÒÔ ‡‚‰ÎË‚Ó Ì ÚÓθÍÓ ‰Îfl Re = Re1 , ÌÓ ‚ Ó·- ˘ÂÏ ÒÎÛ˜‡Â ‰Îfl β·˚ı Re. íÓ„‰‡ u МВ ВТЪ¸ Ф УЛБ‚УО¸МУВ П‡ОУВ ‚УБПЫ˘ВМЛВ, Н‡Н П˚ Ф В‰ОУКЛОЛ ‚˚¯В, ‡ ЛПВВЪ УФ В‰ВОВММУВ НУМВ˜МУВ БМ‡˜ВМЛВ. ЦПЫ ТУУЪ‚ВЪТЪ‚ЫВЪ УФ-В‰ВОВММУВ НУМВ˜МУВ БМ‡˜ВМЛВ ТНУ УТЪЛ ЪВ˜ВМЛfl u = u1 + + u, Ëϲ˘Â„Ó Ô ËÓ‰ 2T.

к‡Т˜ВЪ ‰‡ВЪ δ ≈ 4,67. и ‡‚‰‡, ТОВ‰ЫВЪ Б‡ПВЪЛЪ¸, ˜ЪУВБЫО¸Ъ‡Ъ ТЛО¸МУ Б‡‚ЛТЛЪ УЪ ЪУ˜МУТЪЛ ‚˚˜ЛТОВМЛИ Л

бДдгыуЦзаЦ

н‡НЛП У· ‡БУП, ФУ‰УБ ВМЛfl ФУ‰Ъ‚В ‰ЛОЛТ¸: У‰ЛМ ЛБ ФЫЪВИ ФВ ВıУ‰‡ Н ЪЫ ·ЫОВМЪМУТЪЛ – ТˆВМ‡-ЛИ оВИ„ВМ·‡ЫП‡. зУ ЪУО¸НУ У‰ЛМ ЛБ …, ФУТНУО¸НЫ ВТЪ¸ Л ‰ Ы„ЛВ ТˆВМ‡ ЛЛ. з‡Ф ЛПВ , ВТОЛ Б‡ ЪВ˜ВМЛВП М‡·О˛‰‡Ъ¸ ‰УТЪ‡ЪУ˜МУ ‰УО„У Ф Л ФУТЪУflММ˚ı ЫТОУ‚Лflı, ЪУ ‚ О‡ПЛМ‡ МУП ФУЪУНВ ПУ„ЫЪ ФУfl‚ОflЪ¸Тfl ‚Лı Л ТУ ТОЫ˜‡ИМ˚П ФУ‚В‰ВМЛВП, ФУТОВ ˜В„У Н‡ ЪЛ- М‡ ТМУ‚‡ ТЪ‡МУ‚ЛЪТfl О‡ПЛМ‡ МУИ. н‡НЛП У· ‡БУП, О‡ПЛМ‡ М‡fl Л ı‡УЪЛ˜ВТН‡fl Щ‡Б˚ Ф УˆВТТ‡ ˜В В‰Ы- ˛ЪТfl. н‡НУИ ФВ ВıУ‰ Н ı‡УТЫ МУТЛЪ М‡Б‚‡МЛВ ФВ ВПВ- К‡ВПУТЪЛ. й ТˆВМ‡ Лflı г‡М‰‡Ы Л к˛˝Оfl Л н‡НВМТ‡ П˚ ЫКВ ЫФУПЛМ‡ОЛ. лЫ˘ВТЪ‚Ы˛Ъ „ЛФУЪВБ˚ У ‚УБМЛНМУ‚ВМЛЛ ЪЫ ·ЫОВМЪМУТЪЛ, МВ Т‚flБ‡ММ˚В Т ı‡У- ЪЛ˜ВТНЛПЛ ‡‚ЪУНУОВ·‡МЛflПЛ. й‰М‡ ЛБ ФУТОВ‰МЛı „ЛФУЪВБ, Ф ЛМ‡‰ОВК‡˘‡fl и.л. г‡М‰‡, УТМУ‚‡М‡ М‡ ЪУП, ˜ЪУ Ф ЛМˆЛФЛ‡О¸МЫ˛ УО¸ Л„ ‡˛Ъ ЩОЫНЪЫ‡ˆЛЛ Л ЛПВММУ УМЛ У·ЫТОУ‚ОЛ‚‡˛Ъ М‡·О˛‰‡ВП˚В ЪЫ ·Ы- ОВМЪМ˚В ‚УБПЫ˘ВМЛfl (М‡ФУПМЛП, ‚ ‡‚ЪУНУОВ·‡МЛflıУО¸ ЩОЫНЪЫ‡ˆЛИ П‡О‡).

аТТОВ‰У‚‡МЛfl Ф У‰УОК‡˛ЪТfl, ‡ ЪЫ ·ЫОВМЪМУТЪ¸ МВ ТФВ¯ЛЪ ‡ТН ˚Ъ¸ Т‚УЛ Ъ‡ИМ˚. нВП, НУ„У Б‡ЛМЪВ-ВТУ‚‡О‡ Ф У·ОВП‡, ВНУПВМ‰ЫВП ТФВˆЛ‡О¸М˚И МУПВ КЫ М‡О‡ “аБ‚ВТЪЛfl ‚˚Т¯Лı Ы˜В·М˚ı Б‡‚В‰ВМЛИ. и ЛНО‡‰М‡fl МВОЛМВИМ‡fl ‰ЛМ‡ПЛН‡” ‹ 2 Б‡ 1995 „У‰, ˆВОЛНУП ФУТ‚fl˘ВММ˚И „Л‰ У‰ЛМ‡ПЛ˜ВТНУИ ЪЫ ·Ы- ОВМЪМУТЪЛ Л НУ„В ВМЪМ˚П ТЪ ЫНЪЫ ‡П.

ганЦкДнмкД

1.åÓÙÙ‡Ú É. зВНУЪУ ˚В М‡Ф ‡‚ОВМЛfl ‡Б‚ЛЪЛfl ЪВУ-ЛЛ ЪЫ ·ЫОВМЪМУТЪЛ // лУ‚ ВПВММ‡fl „Л‰ У‰ЛМ‡ПЛН‡: мТФВıЛ Л Ф У·ОВП˚. е.: еЛ , 1984. 501 Т.

2.ä ‡ÈÚ˜ÙËΉ Ñ.è., î‡ Ï ÑÊ.Ñ., è‡Í͇ ‰ ç.ï.,

òÓÛ ê.ë. ï‡ÓÒ // Ç ÏË Â Ì‡ÛÍË. 1987. ‹ 2. ë. 16–28.

3.ä ‡ÈÌÓ‚ Ç.è. д‡˜ВТЪ‚ВММ˚В ПВЪУ‰˚ ‚ ЩЛБЛ˜ВТНУИ НЛМВЪЛНВ Л „Л‰ У‰ЛМ‡ПЛНВ. е.: З˚Т¯. ¯Н., 1989. л. 131–134.

* * *

СПЛЪ ЛИ а‚‡МУ‚Л˜ н Ы·ВˆНУ‚, ‰УНЪУ ЩЛБЛНУ- П‡ЪВП‡ЪЛ˜ВТНЛı М‡ЫН, Ф УЩВТТУ , ˜ОВМ-НУ ВТФУМ‰ВМЪ кУТТЛИТНУИ АН‡‰ВПЛЛ М‡ЫН, Б‡‚. Н‡ЩВ- ‰ УИ ˝ОВНЪ УМЛНЛ Л ‚УОМУ‚˚ı Ф УˆВТТУ‚, ВНЪУ л‡ ‡ЪУ‚ТНУ„У „УТЫ‰‡ ТЪ‚ВММУ„У ЫМЛ‚В ТЛЪВЪ‡ ЛП. з.Й. уВ М˚¯В‚ТНУ„У. й·О‡ТЪ¸ М‡Ы˜М˚ı ЛМЪВ В- ТУ‚: ‡‰ЛУЩЛБЛН‡, Т‚В ı‚˚ТУНУ˜‡ТЪУЪМ‡fl ˝ОВНЪ У- МЛН‡, ЪВУ Лfl НУОВ·‡МЛИ Л ‚УОМ, Ф ЛПВМВМЛВ ПВЪУ- ‰У‚ МВОЛМВИМУИ ‰ЛМ‡ПЛНЛ ‚ ‡БОЛ˜М˚ı У·О‡ТЪflı М‡ЫНЛ. А‚ЪУ Л ТУ‡‚ЪУ 14 ПУМУ„ ‡ЩЛИ Л Ы˜В·М˚ı ФУТУ·ЛИ, ·УОВВ 100 ТЪ‡ЪВИ.