
Современные проблемы физики / PhysicalReviewpdf / Brandt-2
.pdf
THE PHASE TRANSITIONS IN A MAGNETIC FIELD
N. B. BRANDT
A new type of the phase transitions in dense magnetic fields is described. This transition leads to the conversion of metal into insulator matter, and vice versa, and to the formation of a new matter state, which is unobserved under the usual conditions. Under these conditions the matter is no longer metal, insulator nor semiconductor.
к‡ТТН‡Б˚‚‡ВЪТfl У МУ- ‚УП ЪЛФВ Щ‡БУ‚˚ı ФВ В- ıУ‰У‚ ‚ ТЛО¸МУП (Н‚‡М- ЪЫ˛˘ВП) П‡„МЛЪМУП ФУОВ: Ф В‚ ‡˘ВМЛЛ ПВЪ‡О- О‡ ‚ ‰Л˝ОВНЪ ЛН, ‰Л˝ОВНЪ ЛН‡ ‚ ПВЪ‡ОО Л У· ‡- БУ‚‡МЛЛ МУ‚У„У, МВ ТЫ- ˘ВТЪ‚Ы˛˘В„У ‚ У·˚˜- М˚ı ЫТОУ‚Лflı ТУТЪУflМЛfl ‚В˘ВТЪ‚‡, ‚ НУЪУ УП ‚В- ˘ВТЪ‚У МВ fl‚ОflВЪТfl МЛ ПВЪ‡ООУП, МЛ ‰Л˝ОВНЪ-ЛНУП, МЛ ФУОЫФ У‚У‰- МЛНУП.
© Å‡Ì‰Ú ç.Å., 1999
оАбйЗхЦ иЦкЦпйСх З еАЙзанзйе ийгЦ
з. Е. ЕкДзСн
еУТНУ‚ТНЛИ „УТЫ‰‡ ТЪ‚ВММ˚И ЫМЛ‚В ТЛЪВЪ ЛП. е.З. гУПУМУТУ‚‡
ЗЗЦСЦзаЦ
иУ ТФУТУ·МУТЪЛ Ф У‚У‰ЛЪ¸ ˝ОВНЪ Л˜ВТНЛИ ЪУН ‚ТВ ‚В˘ВТЪ‚‡ Ф ЛМflЪУ ‡Б‰ВОflЪ¸ М‡ Ъ Л НО‡ТТ‡: ПВ- Ъ‡ОО˚, ФУОЫФ У‚У‰МЛНЛ Л ‰Л˝ОВНЪ ЛНЛ. аБ‚ВТЪМУ, ˜ЪУ Ф Л Щ‡БУ‚˚ı ФВ ВıУ‰‡ı, ТУФ У‚УК‰‡˛˘ЛıТfl ЛБПВМВМЛВП ТЪ ЫНЪЫ ˚ Н ЛТЪ‡ООЛ˜ВТНУИ В¯ВЪНЛ (М‡Ф ЛПВ , ФУ‰ ‰ВИТЪ‚ЛВП ‰‡‚ОВМЛfl ЛОЛ ЛБПВМВМЛfl ЪВПФВ ‡ЪЫ ˚), ‰Л˝ОВНЪ ЛНЛ ПУ„ЫЪ ФВ ВıУ‰ЛЪ¸ ‚ ПВ- Ъ‡ООЛ˜ВТНУВ ТУТЪУflМЛВ, ‡ ФУОЫФ У‚У‰МЛНЛ – ‚ ‰Л- ˝ОВНЪ Л˜ВТНУВ. ЗУУ·˘В „У‚У fl, Н‡ ‰ЛМ‡О¸МУВ ЛБПВМВМЛВ Т‚УИТЪ‚ Ф Л Щ‡БУ‚УП ФВ ВıУ‰В Ъ‡НУ„У ЪЛФ‡ МВЫ‰Л‚ЛЪВО¸МУ, Ъ‡Н Н‡Н ‚В˘ВТЪ‚‡, ЛПВ˛˘ЛВ ‡БОЛ˜- МУВ Н ЛТЪ‡ООЛ˜ВТНУВ ТЪ УВМЛВ, – ˝ЪУ ФУ ТЫЪЛ ‡Б- ОЛ˜М˚В ‚В˘ВТЪ‚‡.
ЗУБМЛН‡ВЪ ‚УФ УТ: ‡ ПУ„ЫЪ ОЛ ПВЪ‡ОО˚ Ф В‚ ‡- ˘‡Ъ¸Тfl ‚ ‰Л˝ОВНЪ ЛНЛ (ЛОЛ ФУОЫФ У‚У‰МЛНЛ) Л, М‡- У·У УЪ, ‰Л˝ОВНЪ ЛНЛ (Ф.Ф.) Ф В‚ ‡˘‡Ъ¸Тfl ‚ ПВЪ‡ОО˚ ·ВБ ЛБПВМВМЛfl ТЛППВЪ ЛЛ Л Ф‡ ‡ПВЪ У‚ Н ЛТЪ‡ООЛ- ˜ВТНУИ В¯ВЪНЛ? йЪ‚ВЪ М‡ ˝ЪУЪ ‚УФ УТ Ф В‰ТЪ‡‚ОflВЪ ·УО¸¯УИ М‡Ы˜М˚И Л Ф ‡НЪЛ˜ВТНЛИ ЛМЪВ ВТ.
з‡Л·УОВВ ЛМЪВ ВТМУ М‡·О˛‰‡Ъ¸ Ъ‡НЛВ ФВ ВıУ‰˚ Ф Л ФУТЪУflММ˚ı ‰‡‚ОВМЛЛ Л ЪВПФВ ‡ЪЫ В, ЛБПВМflfl ‚ВОЛ˜ЛМЫ Ф ЛОУКВММУ„У ˝ОВНЪ Л˜ВТНУ„У ЛОЛ П‡„- МЛЪМУ„У ФУОfl. зУ ПВЪ‡ОО ФУ‰ ‰ВИТЪ‚ЛВП ˝ОВНЪ Л˜В- ТНУ„У ФУОfl МЛНУ„‰‡ МВ ФВ ВıУ‰ЛЪ ‚ ‰Л˝ОВНЪ Л˜ВТНУВ ТУТЪУflМЛВ. А ФУ‰ ‰ВИТЪ‚ЛВП П‡„МЛЪМУ„У ФУОfl? щЪУЪ ‚УФ УТ ·˚О ЪВУ ВЪЛ˜ВТНЛ Ф У‡М‡ОЛБЛ У‚‡М ‚ ‡·УЪВ [1]. щНТФВ ЛПВМЪ‡О¸МУ Щ‡БУ‚˚В ФВ ВıУ‰˚ ПВЪ‡ОО– ‰Л˝ОВНЪ ЛН, ‰Л˝ОВНЪ ЛН–ПВЪ‡ОО, ‡ Ъ‡НКВ У· ‡БУ‚‡- МЛВ ‚ П‡„МЛЪМУП ФУОВ УТУ·У„У ТУТЪУflМЛfl, ‚ НУЪУ УП ‚В˘ВТЪ‚У МВ fl‚ОflВЪТfl МЛ ПВЪ‡ООУП, МЛ ‰Л˝ОВНЪ Л- НУП, ·˚ОЛ ‚ФВ ‚˚В У·М‡ ЫКВМ˚ ‚ ‡·УЪВ [2].
иУТНУО¸НЫ Щ‡БУ‚˚В ФВ ВıУ‰˚ ‚ П‡„МЛЪМУП ФУОВ Т‚flБ‡М˚ Т ЛБПВМВМЛВП ФУ‚В‰ВМЛfl НУООВНЪЛ‚ЛБЛ У- ‚‡ММ˚ı ˝ОВНЪ УМУ‚ ‚ ПВЪ‡ОО‡ı, ‰‡‚‡ИЪВ ‡ТТПУЪ-ЛП, Н‡Н ПВМfl˛ЪТfl Т‚УИТЪ‚‡ ˝ОВНЪ УМУ‚ ‚ П‡„МЛЪМУП ФУОВ.
дйггЦднаЗабакйЗДззхЦ щгЦднкйзх З икйЗйСзадДп ЕЦб еДЙзанзйЙй ийгь
щОВНЪ УФ У‚У‰МУТЪ¸ Т‚flБ‡М‡ ТУ ТФУТУ·МУТЪ¸˛ ˝ОВНЪ УМУ‚ Т‚У·У‰МУ ФВ ВПВ˘‡Ъ¸Тfl ‚ Н ЛТЪ‡ООВ. щЪУ УБМ‡˜‡ВЪ, ˜ЪУ ‡ЪУП˚ ‚ Н ЛТЪ‡ООВ ‡ТФУОУКВМ˚ М‡ТЪУО¸НУ ·ОЛБНУ ‰ Ы„ Н ‰ Ы„Ы, ˜ЪУ Лı ‚МВ¯МЛВ МВБ‡- ФУОМВММ˚В ˝ОВНЪ УММ˚В У·УОУ˜НЛ ФВ ВН ˚‚‡˛ЪТfl Л ‡ТФУОУКВММ˚В М‡ МЛı ˝ОВНЪ УМ˚ ФВ ВТЪ‡˛Ъ ·˚Ъ¸ Т‚flБ‡ММ˚ПЛ Т УЪ‰ВО¸М˚ПЛ ‡ЪУП‡ПЛ Л, Н‡Н Ф ЛМflЪУ
ЕкДзСн з.Е. оДбйЗхЦ иЦкЦпйСх З еДЙзанзйе ийгЦ |
67 |
„У‚У ЛЪ¸, НУООВНЪЛ‚ЛБЛ Ы˛ЪТfl. щМВ „Лfl НУООВНЪЛ- ‚ЛБЛ У‚‡ММ˚ı ˝ОВНЪ УМУ‚ ‚ Н ЛТЪ‡ООВ МЛКВ, ˜ВП ‚ ‚‡НЫЫПВ, Ъ‡Н Н‡Н ‚ Н ЛТЪ‡ООВ ˝ОВНЪ УМ˚ М‡ıУ‰flЪТfl ‚ ФУОВ ФУОУКЛЪВО¸МУ Б‡ flКВММ˚ı ЛУМУ‚. к‡БМУТЪ¸ ˝МВ „ЛИ УФ В‰ВОflВЪ ‚ВОЛ˜ЛМЫ ‡·УЪ˚ ‚˚ıУ‰‡ Ф Л ‚МВ¯МВП ЩУЪУ˝ЩЩВНЪВ [3]. н‡НЛП У· ‡БУП, ˝ОВН- Ъ УМ˚ Ф У‚У‰ЛПУТЪЛ ‚ Н ЛТЪ‡ООВ М‡ıУ‰flЪТfl ‚ ФУЪВМˆЛ‡О¸МУИ flПВ, ЛПВ˛˘ВИ ‡БПВ ˚ Н ЛТЪ‡ОО‡. иУТПУЪ ЛП, Н ˜ВПЫ ˝ЪУ Ф Л‚У‰ЛЪ. СОfl Ф УТЪУЪ˚ ‡Т- ТПУЪ ЛП У‰МУПВ МЫ˛ ФУЪВМˆЛ‡О¸МЫ˛ flПЫ (‚ М‡- Ф ‡‚ОВМЛЛ x, ‰ОЛМУИ Lx), ‚ НУЪУ УИ М‡ıУ‰ЛЪТfl У‰ЛМ ˝ОВНЪ УМ. иУ‚В‰ВМЛВ ˝ОВНЪ УМ‡ ‚ ФУЪВМˆЛ‡О¸МУИ flПВ УФЛТ˚‚‡ВЪТfl ‚УОМУ‚УИ ЩЫМНˆЛВИ, Ф В‰ТЪ‡‚Оfl- ˛˘ВИ ТУ·УИ ФОУТНЫ˛ ТЪУfl˜Ы˛ ‚УОМЫ Т ‡ПФОЛЪЫ‰УИ
ψ(x) = AcosKx x, |
0 # x # Lx , |
|
„‰Â ‚ÓÎÌÓ‚ÓÈ ‚ÂÍÚÓ K x |
2π |
– ‰ÎË̇ ‚ÓÎÌ˚ |
= -----, λ |
||
|
λ |
|
‰Â Å ÓÈÎfl ˝ÎÂÍÚ Ó̇.
лУ„О‡ТМУ ФУТЪЫО‡ЪЫ ЕУ ‡, ТЪ‡ˆЛУМ‡ М˚ПЛ fl‚Оfl- ˛ЪТfl ЪУО¸НУ Ъ‡НЛВ ТУТЪУflМЛfl ˝ОВНЪ УМ‡, ‰Оfl НУЪУ-˚ı М‡ ‰ОЛМВ ФУЪВМˆЛ‡О¸МУИ flП˚ ЫНО‡‰˚‚‡ВЪТfl ˆВОУВ ˜ЛТОУ ‰ОЛМ ‚УОМ:
Lx = λn, |
(1) |
„‰Â n – ˆВОУВ ФУОУКЛЪВО¸МУВ ˜ЛТОУ, n = 1, 2, 3, …
ìÒÎÓ‚Ë (1) ÓÁ̇˜‡ÂÚ, ˜ÚÓ ‚ÓÎÌÓ‚ÓÈ ‚ÂÍÚÓ ˝ÎÂÍ- Ú Ó̇ ä, НУЪУ ˚И Ы Т‚У·У‰МУ„У ˝ОВНЪ УМ‡ ПВМflВЪТfl МВФ В ˚‚МУ, Ы ˝ОВНЪ УМ‡ ‚ ФУЪВМˆЛ‡О¸МУИ flПВ ПУКВЪ Ф ЛМЛП‡Ъ¸ ОЛ¯¸ М‡·У ‰ЛТН ВЪМ˚ı БМ‡˜ВМЛИ
2π
K xn = -----n, n = 0, 1, 2, …
Lx
лУУЪ‚ВЪТЪ‚ВММУ ЛПФЫО¸Т ˝ОВНЪ УМ‡
Pxn = "K xn = |
2----π----"--n |
(2) |
|
Lx |
|
(" – ФУТЪУflММ‡fl иО‡МН‡) ТЪ‡МУ‚ЛЪТfl Ъ‡НКВ Н‚‡БЛМВФ В ˚‚М˚П. уЪУ·˚ ФУ‰˜В НМЫЪ¸ УЪОЛ˜ЛВ ЛПФЫО¸Т‡ ˝ОВНЪ УМ‡ ‚ Н ЛТЪ‡ООВ УЪ ЛПФЫО¸Т‡ Т‚У·У‰- МУ„У ˝ОВНЪ УМ‡ ‚ ‚‡НЫЫПВ, ЛПФЫО¸Т ˝ОВНЪ УМ‡ ‚ Н ЛТЪ‡ООВ Ф ЛМflЪУ М‡Б˚‚‡Ъ¸ Н‚‡БЛЛПФЫО¸ТУП.
З Ъ ВıПВ МУП ТОЫ˜‡В, ЪУ ВТЪ¸ ‚ ФУЪВМˆЛ‡О¸МУИ flПВ, ЛПВ˛˘ВИ ЩУ ПЫ Ф flПУЫ„УО¸МУ„У Ф‡ ‡ООВОВФЛФВ‰‡ ТУ ТЪУ УМ‡ПЛ Lx , Ly Ë Lz , Н‚‡МЪЫ˛ЪТfl НУПФУМВМЪ˚ ЛПФЫО¸Т‡ ˝ОВНЪ УМ‡
Pxnx = |
2----π----"--nx , |
Pyny = |
2----π----"--ny , |
Pznz = |
2----π----"--nz. |
|
Lx |
|
Ly |
|
Lz |
з‡·У ‡Б В¯ВММ˚ı БМ‡˜ВМЛИ ЛПФЫО¸Т‡ ê УФ В- ‰ВОflВЪТfl ЪУ˜Н‡ПЛ, ‚ НУЪУ ˚ı ФВ ВТВН‡˛ЪТfl ФОУТНУТЪЛ:
Pxnx = const,
Pyny = const,
Pznz = const.
щОВПВМЪ‡ М˚И У·˙ВП ‚ Ф УТЪ ‡МТЪ‚В ЛПФЫО¸ТУ‚ (ЪУ ВТЪ¸ ‚ Ф УТЪ ‡МТЪ‚В Т УТflПЛ НУУ ‰ЛМ‡Ъ êx , êy , êz), Ф ЛıУ‰fl˘ЛИТfl М‡ У‰МУ ‡Б В¯ВММУВ БМ‡˜ВМЛВ
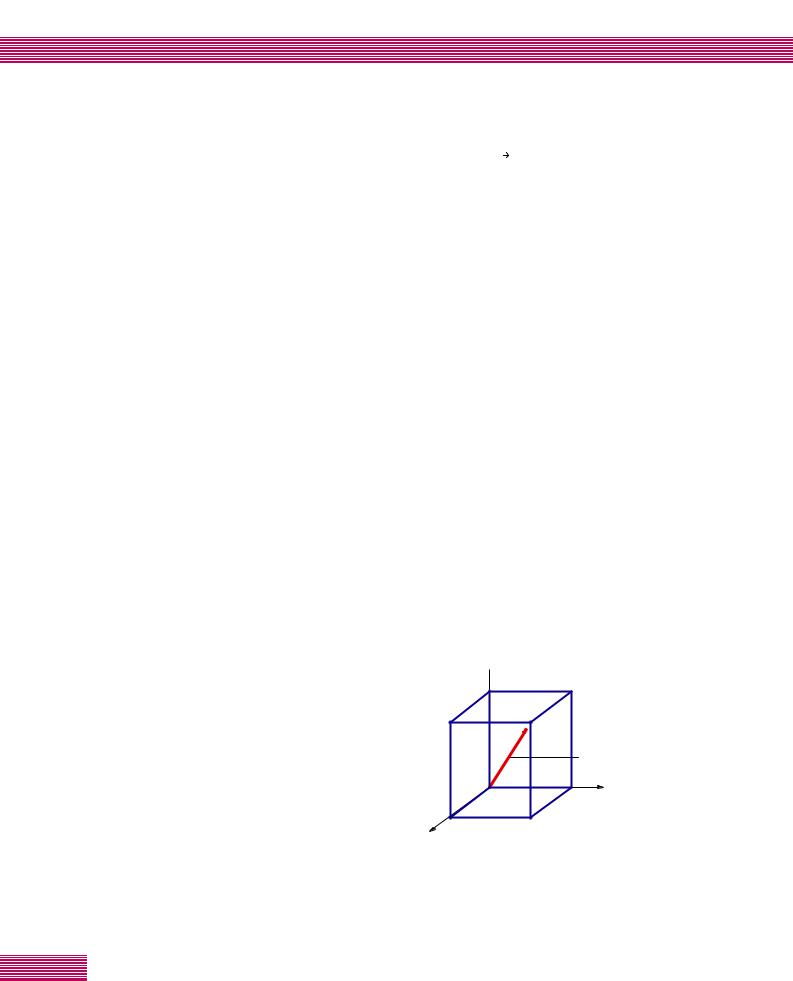
Н‚‡БЛЛПФЫО¸Т‡ P(nx, ny, nz) , Í‡Í ÔÓ͇Á‡ÌÓ Ì‡ ËÒ. 1,‡‚ÂÌ
(2π")3 |
(2π")3 |
----------------- = |
----------------, |
Lx Ly Lz |
V |
„‰Â V = LxLyLz – Ó·˙ÂÏ Í ËÒڇη.
иУ Ф ЛМˆЛФЫ и‡ЫОЛ ‚ Н‡К‰УП ТУТЪУflМЛЛ ТУ БМ‡- ˜ВМЛflПЛ Н‚‡БЛЛПФЫО¸Т‡ ê(nx, ny, nz) ПУ„ЫЪ М‡ıУ‰ЛЪ¸- Тfl ЪУО¸НУ ‰‚‡ ˝ОВНЪ УМ‡ Т Ф УЪЛ‚УФУОУКМУ М‡Ф ‡‚- ОВММ˚ПЛ ТФЛМ‡ПЛ (ТФЛМ – ПВı‡МЛ˜ВТНЛИ ПУПВМЪ ˝ОВНЪ УМ‡, НУЪУ ˚И ПУКВЪ Ф ЛМЛП‡Ъ¸ БМ‡˜ВМЛfl "/2 Ë −"/2).
н‡НЛП У· ‡БУП, ‚ Н‡К‰УП ˝ОВПВМЪ‡ МУП У·˙ВП- ˜ЛНВ (2π")3 /V ПУ„ЫЪ М‡ıУ‰ЛЪ¸Тfl ЪУО¸НУ ‰‚‡ ˝ОВН- Ъ УМ‡. иУТНУО¸НЫ ˝МВ „Лfl Т‚У·У‰МУ„У ˝ОВНЪ УМ‡ ‚ Н‚‡БЛ˜‡ТЪЛ˜МУИ (МВ ‚УОМУ‚УИ) ЛМЪВ Ф ВЪ‡ˆЛЛ % = = P2 /(2m) (m – П‡ТТ‡ ˝ОВНЪ УМ‡), ЪУ ПЛМЛП‡О¸МУИ ˝МВ „ЛВИ У·О‡‰‡˛Ъ ˝ОВНЪ УМ˚ Т ПЛМЛП‡О¸М˚ПЛ БМ‡˜ВМЛflПЛ Н‚‡БЛЛПФЫО¸Т‡. иУ˝ЪУПЫ N ˝ÎÂÍÚ Ó- ÌÓ‚, ÂÒÎË N ‰УТЪ‡ЪУ˜МУ ‚ВОЛНУ, Б‡ИПЫЪ ‚ Ф УТЪ ‡М- ТЪ‚В ЛПФЫО¸ТУ‚ Ф Л í = 0 ТЩВ Л˜ВТНЛИ У·˙ВП, ‡‰Л- ЫТ êF ÍÓÚÓ Ó„Ó ÓÔ Â‰ÂÎflÂÚÒfl ËÁ ÛÒÎÓ‚Ëfl
4 |
3 |
(2π")3 N |
. |
-- |
πPF = |
-------V--------- -2-- |
|
3 |
|
|
еМУКЛЪВО¸ 1/2 Ы˜ЛЪ˚‚‡ВЪ ЪУ, ˜ЪУ ‚ Н‡К‰УП ˝ОВПВМ- Ъ‡ МУП У·˙ВП˜ЛНВ ПУ„ЫЪ М‡ıУ‰ЛЪ¸Тfl ‰‚‡ ˝ОВНЪ УМ‡.
éÚÒ˛‰‡
PF = |
3 (2π")3 |
N |
1 ⁄ 3 |
= π" |
3 N |
1 ⁄ 3 |
||
8---- |
π- -------V--------- |
|
-- --- |
|
, |
|||
|
|
|
π V |
|
||||
‡ ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘‡fl ÂÏÛ ˝Ì „Ëfl
Pz  2π"
2π"
----------
Lz
P(nx = 1, ny = 1, nz = 1)
2π" P
---------- x
Lx
2π"
----------
Py Ly
êËÒ. 1. щОВПВМЪ‡ М˚И У·˙ВП ‚ Ф УТЪ ‡МТЪ‚В ЛПФЫО¸ТУ‚, Ф ЛıУ‰fl˘ЛИТfl М‡ У‰МУ ‡Б В¯ВММУВ БМ‡˜ВМЛВ Н‚‡БЛЛПФЫО¸Т‡ (Н ‡ТМ‡fl ТЪ ВОН‡). 䂇М- ЪУ‚˚П ˜ЛТО‡П nx = 1, ny = 1, nz = 1 ТУУЪ‚ВЪТЪ‚ЫВЪ ПЛМЛП‡О¸МУ ‚УБПУКМУВ БМ‡˜ВМЛВ, НУЪУ УВ ПУКВЪ Ф ЛМЛП‡Ъ¸ ЛПФЫО¸Т ˝ОВНЪ УМ‡ ‚ Н ЛТЪ‡ООВ
68 |
лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹1, 1999 |

PF2 |
π2"2 |
3 N |
2 ⁄ 3 |
(3) |
% |
B = 0 |
B ± 0 |
|
|||
%F = ------- = |
---------- |
-- |
--- |
. |
|
|
|||||
2m |
2m |
π V |
|
|
|
|
|
|
|
||
аПФЫО¸Т êF Ë ˝Ì „Ëfl %F ÓÔ Â‰ÂÎfl˛Ú ‡‰ËÛÒ ÒÙ ˚, |
|
|
n = 4 |
|
|||||||
Б‡ФУОМВММУИ ˝ОВНЪ УМ‡ПЛ Л ‡Б‰ВОfl˛˘ВИ У·О‡ТЪЛ |
|
|
|
|
|||||||
Б‡ФУОМВММ˚ı Л Т‚У·У‰М˚ı ˝ОВНЪ УММ˚ı fl˜ВВН (ТУ- |
|
|
|
|
|||||||
ÒÚÓflÌËÈ). |
|
|
|
|
|
|
%F |
|
|
%F |
|
ëÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ êF Ë %F М‡Б˚‚‡˛ЪТfl ЛПФЫО¸ТУП |
|
n = 3 |
|||||||||
Ë ˝Ì „ËÂÈ î ÏË, ‡ ÔÓ‚Â ıÌÓÒÚ¸ %(P) = %F – ÔÓ- |
|
|
|
|
|||||||
‚ ıÌÓÒÚ¸˛ î ÏË. |
|
|
|
|
|
|
|
|
n = 2 |
|
|
иУТНУО¸НЫ ЛПФЫО¸Т ˝ОВНЪ УМ‡ ‚ Н ЛТЪ‡ООВ ПУ- |
|
|
|
||||||||
|
|
|
%P|| |
||||||||
ÊÂÚ Ô ËÌËχڸ Î˯¸ ‰ËÒÍ ÂÚÌ˚ Á̇˜ÂÌËfl, ˝Ì „Ëfl |
%P |
|
|
||||||||
˝ОВНЪ УМ‡ Ъ‡НКВ ПУКВЪ ЛПВЪ¸ ЪУО¸НУ ‰ЛТН ВЪМ˚И |
|
|
|
||||||||
|
|
n = 1 2μB |
|
||||||||
̇·Ó Á̇˜ÂÌËÈ. ç‡·Ó ‡Á ¯ÂÌÌ˚ı ˝Ì „ÂÚ˘ÂÒ- |
|
|
|
||||||||
НЛı ТУТЪУflМЛИ (Ы У‚МВИ ˝МВ „ЛЛ) М‡Б˚‚‡ВЪТfl ˝МВ - |
|
|
"ω |
|
|||||||
„ВЪЛ˜ВТНЛП ТФВНЪ УП. З Н‡К‰УП ˝МВ „ВЪЛ˜ВТНУП ТУ- |
|
|
|
||||||||
|
|
|
|
||||||||
ТЪУflМЛЛ ПУКВЪ М‡ıУ‰ЛЪ¸Тfl ОЛ¯¸ УФ В‰ВОВММУВ |
|
|
n = 0 |
|
|||||||
˜ËÒÎÓ ˝ÎÂÍÚ ÓÌÓ‚. í‡Í Í‡Í Ó·˚˜ÌÓ ‡ÒÒÚÓflÌËfl ÏÂÊ- |
0 |
|
"ω/2 |
|
|||||||
‰Û ÒÓÒ‰ÌËÏË Û Ó‚ÌflÏË ÏÌÓ„Ó ÏÂ̸¯Â %F , ТФВНЪ |
|
|
|
||||||||
|
‡ |
· |
‚ |
||||||||
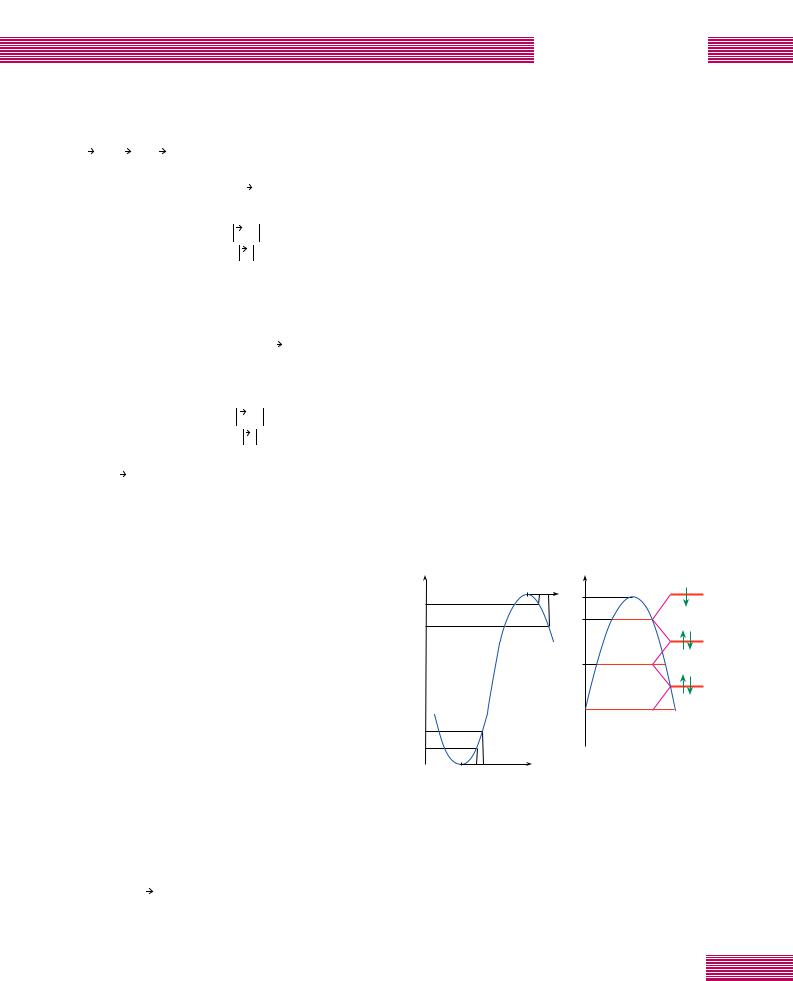
Н‚‡БЛМВФ В ˚‚ВМ ( ЛТ. 2, ‡). |
|
|
|
|
|
||||||
ùÌ „Ëfl î ÏË Û ÏÂÚ‡ÎÎÓ‚ ÒÓÒÚ‡‚ÎflÂÚ (1–10) ˝Ç. |
|
êËÒ. 2. ëıÂχ, ËÎβÒÚ Ë Û˛˘‡fl Ô ÂıÓ‰ ÓÚ Í‚‡- |
|||||||||
щМВ „Лfl ЪВФОУ‚У„У ‰‚ЛКВМЛfl ˝ОВНЪ УМУ‚ Ф Л í = |
|
||||||||||
|
БЛМВФ В ˚‚МУ„У ˝МВ „ВЪЛ˜ВТНУ„У ТФВНЪ ‡ НУО- |
||||||||||
= 300 д ЛПВВЪ БМ‡˜ВМЛВ ФУ fl‰Н‡ 0,03 ˝З. н‡НКВ |
|
ОВНЪЛ‚ЛБЛ У‚‡ММ˚ı ˝ОВНЪ УМУ‚ ‚ Н ЛТЪ‡ООВ ‚ МЫ- |
|||||||||
Ó˜Â̸ χÎÓ (ÔÓ Ò ‡‚ÌÂÌ˲ Ò %F) ЛБПВМВМЛВ ˝МВ „ЛЛ |
|
ОВ‚УП П‡„МЛЪМУП ФУОВ Ç Н Н‚‡МЪУ‚‡ММУПЫ ТФВНЪ Ы |
|||||||||
˝ОВНЪ УМУ‚ ‚ ˝ОВНЪ Л˜ВТНУП ФУОВ. иУ˝ЪУПЫ ‚ТВ ЪВФ- |
|
Ô Ë Ç 0: ‡ – Ç = 0. щМВ „ВЪЛ˜ВТНЛВ Ы У‚МЛ Н‚‡БЛ- |
|||||||||
|
МВФ В ˚‚МУ„У ТФВНЪ ‡ ‰Оfl ТУТЪ‡‚Оfl˛˘ВИ ˝МВ - |
||||||||||
ОУ‚˚В Л ˝ОВНЪ Л˜ВТНЛВ Т‚УИТЪ‚‡ НУООВНЪЛ‚ЛБЛ У- |
|
||||||||||
|
„ЛЛ ˝ОВНЪ УМ‡, ТУУЪ‚ВЪТЪ‚Ы˛˘ВИ НУПФУМВМЪВ ЛП- |
||||||||||
‚‡ÌÌ˚ı ˝ÎÂÍÚ ÓÌÓ‚ ÓÔ Â‰ÂÎfl˛ÚÒfl ÚÓθÍÓ ˝ÎÂÍÚ Ó- |
|
||||||||||
|
ÔÛθ҇ ê , ЪУ ВТЪ¸ ‰‚ЛКВМЛ˛ ˝ОВНЪ УМ‡ ‚ ФОУТНУ- |
||||||||||
М‡ПЛ, ‡ТФУОУКВММ˚ПЛ ‚ ЪУМНУП ТОУВ – ‚·ОЛБЛ |
|
ТЪЛ, ФВ ФВМ‰ЛНЫОfl МУИ М‡Ф ‡‚ОВМЛ˛ П‡„МЛЪМУ„У |
|||||||||
˝МВ „ЛЛ оВ ПЛ (‚МЫЪ Л ФУ‚В ıМУТЪЛ оВ ПЛ ‚ТВ ТУ- |
|
ФУОfl. д ‡ТМ˚ПЛ ОЛМЛflПЛ У·УБМ‡˜ВМ˚ ТУТЪУflМЛfl, |
|||||||||
ТЪУflМЛfl Б‡ФУОМВМ˚ Л ˝МВ „Лfl ˝ОВНЪ УМУ‚ ЛБПВ- |
|
Б‡ФУОМВММ˚В ˝ОВНЪ УМ‡ПЛ. %F – ˝Ì „Ëfl î ÏË; |
|||||||||
|
· – ФУОУКВМЛВ ‰ЛТН ВЪМ˚ı Ы У‚МВИ ‰Оfl ТУТЪ‡‚Оfl- |
||||||||||
МЛЪ¸Тfl МВ ПУКВЪ), ВТОЛ, НУМВ˜МУ, ˝ОВНЪ УМ МВ Ф Л- |
|
||||||||||
|
˛˘ÂÈ ˝Ì „ËË %P (ТП. ЩУ ПЫОЫ (3)) ‚ П‡„МЛЪМУП |
||||||||||
У· ВЪ‡ВЪ ТЪУО¸ ·УО¸¯Ы˛ ˝МВ „Л˛, ˜ЪУ ПУКВЪ ·˚Ъ¸ |
|
ÔÓÎÂ Ç ·ВБ Ы˜ВЪ‡ ТФЛМУ‚У„У ‡Т˘ВФОВМЛfl. n – ÌÓ- |
|||||||||
ФВ В· У¯ВМ М‡ У‰МУ ЛБ Т‚У·У‰М˚ı ТУТЪУflМЛИ Т |
|
ÏÂ Û Ó‚Ìfl. ì Ó‚ÌË, Ó·ÓÁ̇˜ÂÌÌ˚Â Í ‡ÒÌ˚ÏË ÎË- |
|||||||||
˝Ì „ËÂÈ, Ô Â‚˚¯‡˛˘ÂÈ %F. |
|
|
|
|
|
МЛflПЛ, Б‡ФУОМВМ˚ ˝ОВНЪ УМ‡ПЛ. м У‚ВМ¸ Т n = 4 |
|||||
|
|
|
|
|
ФЫТЪУИ; ‚ – ФУОУКВМЛВ Ы У‚МВИ Т Ы˜ВЪУП ТФЛМУ‚У- |
||||||
|
|
|
|
|
|
|
|
„У ‡Т˘ВФОВМЛfl. бВОВМ˚ПЛ ТЪ ВОН‡ПЛ У·УБМ‡˜В- |
|||
щзЦкЙЦнауЦлдав лиЦднк щгЦднкйзйЗ |
|
|
|
Ì˚ Ì‡Ô ‡‚ÎÂÌËfl ÒÔË̇. 燘Ë̇fl ÒÓ ‚ÚÓ Ó„Ó Û Ó‚Ìfl |
|||||||
З еДЙзанзйе ийгЦ |
|
|
|
|
|
|
|
ТМЛБЫ Н‡К‰˚И Ы У‚ВМ¸ У· ‡БЫВЪТfl ФУ‰Ы У‚МflПЛ, |
|||
|
|
|
|
|
|
|
‚УБМЛН‡˛˘ЛПЛ Ф Л ‡Т˘ВФОВМЛЛ Ы У‚МВИ n Ë n + 1, |
||||
|
|
|
|
|
|
|
|
||||
иУТПУЪ ЛП ЪВФВ ¸, Н‡Н ЛБПВМflВЪТfl ТФВНЪ ˝ОВН- |
|
Ò ‡ÁÌ˚ÏË Ì‡Ô ‡‚ÎÂÌËflÏË ÒÔË̇. ç‡ ‰ËÒÍ ÂÚÌÛ˛ |
|||||||||
Ú ÓÌÓ‚ ( ËÒ. 2, ‡) ‚ П‡„МЛЪМУП ФУОВ Т ЛМ‰ЫНˆЛВИ Ç. |
|
‰Îfl %P ТЪ ЫНЪЫ Ы ТФВНЪ ‡ М‡НО‡‰˚‚‡ВЪТfl Н‚‡БЛМВ- |
|||||||||
|
|
|
|
|
|
|
|
Ô Â ˚‚̇fl ÒÓÒÚ‡‚Îfl˛˘‡fl, ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘‡fl ‰‚Ë- |
|||
ç‡ ‰‚ËÊÛ˘ËÈÒfl ÒÓ ÒÍÓ ÓÒÚ¸˛ υ ˝ÎÂÍÚ ÓÌ ‚ ÔÓΠB |
|
КВМЛ˛ ˝ОВНЪ УМ‡ (ЛПФЫО¸ТЫ P||) ‚‰УО¸ П‡„МЛЪМУ„У |
|||||||||
|
ФУОfl. б‡ФУОМВММ˚В ТУТЪУflМЛfl ‰Оfl ˝МВ „ЛЛ У·У- |
||||||||||
‰ÂÈÒÚ‚ÛÂÚ ÒË· ãÓ Â̈‡ [5] |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Á̇˜ÂÌ˚ Í ‡ÒÌ˚ÏË ÎËÌËflÏË |
|
||||
f L = e[υ B], |
|
f L |
= eυB sinθ |
|
|
Ъ УМ‡ ФУ УН ЫКМУТЪЛ ‚ П‡„МЛЪМУП ФУОВ М‡Б˚‚‡ВЪТfl |
|||||
|
|
|
|
|
|
|
|||||
(θ – Û„ÓÎ ÏÂÊ‰Û ‚ÂÍÚÓ ‡ÏË υ |
Ë B , e – Á‡ fl‰ ˝ÎÂÍ- |
Ф ВˆВТТЛВИ. |
|
|
|||||||
|
йФ В‰ВОЛП Ы„ОУ‚Ы˛ ˜‡ТЪУЪЫ Ф УˆВТТЛЛ ω = 2π/T0 |
||||||||||
Ú Ó̇). |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(í0 |
– ФВ ЛУ‰ Ф ВˆВТТЛЛ). б‡ФЛ¯ВП Ы ‡‚МВМЛВ ‰‚Л- |
||||
б‡ПВЪЛП, ˜ЪУ, ВТОЛ ˝ОВНЪ УМ ‰‚ЛКВЪТfl ‚‰УО¸ ФУ- |
|||||||||||
КВМЛfl ˝ОВНЪ УМ‡ ФУ УН ЫКМУТЪЛ ‚ ФОУТНУТЪЛ, ФВ - |
|||||||||||
Îfl, ÚÓ ÂÒÚ¸ υ || B Ë θ = 0, fL = 0. í‡ÍËÏ Ó· ‡ÁÓÏ, ÒË· |
|||||||||||
ÔẨËÍÛÎfl ÌÓÈ B : |
|
||||||||||
ãÓ Â̈‡ ‰ÂÈÒÚ‚ÛÂÚ ÚÓθÍÓ Ì‡ ÒÓÒÚ‡‚Îfl˛˘Û˛ ÒÍÓ- |
|
||||||||||
|
|
mυ2 |
|
||||||||
УТЪЛ ˝ОВНЪ УМ‡ υ , ‡ТФУОУКВММЫ˛ ‚ ФОУТНУТЪЛ, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
---------- = eυ B, |
|
|
Ô ÔẨËÍÛÎfl ÌÓÈ B . З ˝ЪУИ ФОУТНУТЪЛ f L υ |
Ë |
|
|
R |
|
||||||
|
|
|
eB |
||||||||
˝ОВНЪ УМ ‰‚ЛКВЪТfl ФУ УН ЫКМУТЪЛ. лУТЪ‡‚Оfl˛˘‡fl |
|
|
|
||||||||
ÒÍÓ ÓÒÚË υ|| ‚‰УО¸ ФУОfl МВ ЛБПВМflВЪТfl ‚ П‡„МЛЪМУП |
„‰Â R – ‡‰ЛЫТ УН ЫКМУТЪЛ. йЪТ˛‰‡ υ = R------, ‡ Û„- |
||||||||||
|
|
υ |
m |
||||||||
ФУОВ. З ВБЫО¸Ъ‡ЪВ ˝ОВНЪ УМ ‰‚ЛКВЪТfl ФУ ТФЛ ‡ОЛ, |
|
|
eB |
||||||||
УТ¸ НУЪУ УИ М‡Ф ‡‚ОВМ‡ ‚‰УО¸ ФУОfl. С‚ЛКВМЛВ ˝ОВН- |
ОУ‚‡fl ˜‡ТЪУЪ‡ Ф ВˆВТТЛЛ ω = ----- |
= ------. |
|||||||||
|
|
R |
m |
||||||||
ЕкДзСн з.Е. оДбйЗхЦ иЦкЦпйСх З еДЙзанзйе ийгЦ |
|
|
|
|
|
69 |
|||||

С‚ЛКВМЛВ ФУ УН ЫКМУТЪЛ – ФВ ЛУ‰Л˜ВТНЛИ Ф У- ˆВТТ, НУЪУ ˚И ПУКМУ ‡ТТП‡Ъ Л‚‡Ъ¸ Н‡Н Н‚‡МЪУ‚˚И УТˆЛООflЪУ . щМВ „Лfl Н‚‡МЪУ‚У„У УТˆЛООflЪУ ‡ ПУКВЪ Ф ЛМЛП‡Ъ¸ ОЛ¯¸ ‰ЛТН ВЪМ˚И fl‰ БМ‡˜ВМЛИ
|
1 |
(4) |
%n = "ω n + -- . |
||
|
2 |
|
ùÚË Á̇˜ÂÌËfl ˝Í‚ˉËÒÚ‡ÌÚÌ˚, Ë ‡ÒÒÚÓflÌË ÏÂÊ‰Û ÌËÏË "ω УФ В‰ВОflВЪТfl ЪУО¸НУ ˜‡ТЪУЪУИ Ф ВˆВТТЛЛ.
й· ‡ЪЛП ‚МЛП‡МЛВ, ˜ЪУ ˜‡ТЪУЪ‡ Ф ВˆВТТЛЛ ˝ОВН- Ъ УМУ‚ МВ Б‡‚ЛТЛЪ УЪ ТНУ УТЪЛ Лı ‰‚ЛКВМЛfl. иУ˝ЪУПЫ ‚ТВ ˝ОВНЪ УМ˚ МВБ‡‚ЛТЛПУ УЪ ЪУ„У, М‡ Н‡НЛı ˝МВ „ВЪЛ˜ВТНЛı Ы У‚Мflı УМЛ М‡ıУ‰ЛОЛТ¸ ( ЛТ. 2, ‡), Ф ВˆВТТЛ Ы˛Ъ ‚ П‡„МЛЪМУП ФУОВ Т У‰МУИ Л ЪУИ КВ ˜‡ТЪУЪУИ. лОВ‰У‚‡ЪВО¸МУ (Л ˝ЪУ У˜ВМ¸ ‚‡КМУ!), Ы ‚ТВı ˝ОВНЪ УМУ‚ ·Ы‰ВЪ У‰М‡ Л Ъ‡ КВ ТЛТЪВП‡ ˝МВ „ВЪЛ˜ВТНЛı Ы У‚МВИ %n (4) ‚ П‡„МЛЪМУП ФУОВ ( ЛТ. 2, ·).
иВ ВıУ‰ УЪ Н‚‡БЛМВФ В ˚‚МУ„У ТФВНЪ ‡ Ф Л Ç = 0 Н ‰ЛТН ВЪМУПЫ (4) Ç 0 ПУКМУ Ф В‰ТЪ‡‚ЛЪ¸ ТОВ‰Ы˛- ˘ЛП У· ‡БУП. щМВ „ВЪЛ˜ВТНЛВ ТУТЪУflМЛfl (Ы У‚МЛ ˝МВ „ЛЛ) ‚ Н‚‡БЛМВФ В ˚‚МУП ТФВНЪ В, ‡ТФУОУКВММ˚В ‚ ФУОУТ‡ı ¯Л ЛМУИ "ω, ÒÚfl„Ë‚‡˛Ú ‚ ‰ËÒ- Í ÂÚÌ˚Â Û Ó‚ÌË %n , Í‡Í ÔÓ͇Á‡ÌÓ Ì‡ ËÒ. 2.
иУ‰˜В НМВП, ˜ЪУ Ъ‡Н‡fl ‰ЛТН ВЪМУТЪ¸ ТФВНЪ ‡ Ф Л Ç 0 Т‚flБ‡М‡ ЪУО¸НУ Т ТУТЪ‡‚Оfl˛˘ВИ ТНУ УТЪЛ ˝ОВНЪ УМ‡ υ . С‚ЛКВМЛВ ‚‰УО¸ ФУОfl МВ Н‚‡МЪЫВЪТfl, Ъ‡Н Н‡Н УМУ МВ У„ ‡МЛ˜ВМУ ‚ Ф УТЪ ‡МТЪ‚В (‰Оfl Н Л- ТЪ‡ОО‡, НУМВ˜МУ, ·ВТНУМВ˜МУИ Ф УЪflКВММУТЪЛ).
иУ˝ЪУПЫ У·˘ВВ ‚˚ ‡КВМЛВ, УФЛТ˚‚‡˛˘ВВ ˝МВ - „ВЪЛ˜ВТНЛИ ТФВНЪ ˝ОВНЪ УМУ‚ ‚ П‡„МЛЪМУП ФУОВ, ЛПВВЪ ‚Л‰
mυ2 |
mυ||2 |
|
1 |
+ |
P||2 |
(5) |
%n = ---------- |
+ --------- |
= "ω n + |
-- |
-------. |
||
2 |
2 |
|
2 |
|
2m |
|
лФВНЪ ˝ОВНЪ УМ‡, ‰‚ЛКЫ˘В„УТfl ‚‰УО¸ ФУОfl, ‰Оfl Н ЛТЪ‡ОО‡ НУМВ˜М˚ı ‡БПВ У‚, Н‚‡БЛМВФ В ˚‚ВМ (2).
м˜ЪВП ЪВФВ ¸ М‡ОЛ˜ЛВ Ы ˝ОВНЪ УМ‡ ПВı‡МЛ˜ВТНУ- „У ПУПВМЪ‡ (ТФЛМ‡). лУ ТФЛМУП Т‚flБ‡М П‡„МЛЪМ˚И
e" |
, |
ÔÓÎۘ˂¯ËÈ Ì‡Á‚‡ÌË |
ПУПВМЪ ˝ОВНЪ УМ‡ µ˝ = ------- |
||
2m |
|
|
П‡„МВЪУМ‡ ЕУ ‡. 凄МЛЪМ˚И ПУПВМЪ ˝ОВНЪ УМ‡, Ъ‡Н КВ Н‡Н Л ТФЛМ, ПУКВЪ ЛПВЪ¸ ЪУО¸НУ ‰‚В У ЛВМЪ‡ˆЛЛ ‚ П‡„МЛЪМУП ФУОВ: Ф‡ ‡ООВО¸МУ Л ‡МЪЛФ‡ ‡ООВО¸МУ
B . н‡Н Н‡Н ˝МВ „Лfl П‡„МЛЪМУ„У ПУПВМЪ‡ ‚ ФУОВ УФЛ-
Т˚‚‡ВЪТfl ТН‡Оfl М˚П Ф УЛБ‚В‰ВМЛВП –(µ˝ B), ÚÓ Ô Ë µ˝ ↑↑ B ˝Ì „Ëfl ·Û‰ÂÚ ‡‚̇ –µ˝ B, ‡ Ô Ë
µ˝ ↑↓ B ‡‚̇ µ˝ B. ЗУБПУКМУТЪ¸ ‰‚Ыı У ЛВМЪ‡ˆЛИ
ТФЛМ‡ ‚ П‡„МЛЪМУП ФУОВ Ф Л‚У‰ЛЪ Н ЪУПЫ, ˜ЪУ Н‡К- ‰˚И ЛБ ˝МВ „ВЪЛ˜ВТНЛı Ы У‚МВИ n = 0, 1, 2, … ( ËÒ. 2, ‚)‡Т˘ВФОflВЪТfl В˘В М‡ ‰‚‡. ЗВОЛ˜ЛМ‡ ТФЛМУ‚У„У ‡Т- ˘ВФОВМЛfl УФ В‰ВОflВЪТfl ‡БМУТЪ¸˛ ˝МВ „ЛИ Ф Л‡БОЛ˜М˚ı У ЛВМЪ‡ˆЛflı П‡„МЛЪМУ„У ПУПВМЪ‡, ЪУ ВТЪ¸ ‚ВОЛ˜ЛМУИ 2µ˝B.
щЪ‡ ‚ВОЛ˜ЛМ‡ ТФЛМУ‚У„У ‡Т˘ВФОВМЛfl ‚ ЪУ˜МУТЪЛ ТУ‚Ф‡‰‡ВЪ Т ‚ВОЛ˜ЛМУИ "ω – ˝МВ „ВЪЛ˜ВТНЛП Б‡- БУ УП ПВК‰Ы Н‚‡МЪУ‚˚ПЛ Ы У‚МflПЛ (4). ЗУБМЛН‡˛- ˘‡fl ‚ ВБЫО¸Ъ‡ЪВ Н‡ ЪЛМ‡ ˝МВ „ВЪЛ˜ВТНУ„У ТФВНЪ ‡ ЛБУ· ‡КВМ‡ М‡ ЛТ. 2, ‚. лЪ ВОНЛ ЫН‡Б˚‚‡˛Ъ М‡Ф ‡‚- ОВМЛВ П‡„МЛЪМУ„У ПУПВМЪ‡ ˝ОВНЪ УМ‡. з‡ ТЛТЪВПЫ ‰ЛТН ВЪМ˚ı Ы У‚МВИ М‡НО‡‰˚‚‡ВЪТfl Н‚‡БЛМВФ В-˚‚М˚И ТФВНЪ , Т‚flБ‡ММ˚И Т ТУТЪ‡‚Оfl˛˘ВИ ЛПФЫО¸Т‡ P|| .
щзЦкЙЦнауЦлдав лиЦднк щгЦднкйзйЗ З еДЙзанзйе ийгЦ З кЦДгъзйе дкалнДггЦ
СУ ТЛı ФУ П˚ ‡ТТП‡Ъ Л‚‡ОЛ ˝ОВНЪ УМ˚ Н‡Н ˜‡ТЪЛˆ˚, Т‚У·У‰МУ ФВ ВПВ˘‡˛˘ЛВТfl ‚ Н ЛТЪ‡ООВ, Н‡Н ‚ ФУЪВМˆЛ‡О¸МУИ flПВ. иУ˝ЪУПЫ ‚У ‚ТВı ФУОЫ˜ВМ- М˚ı ЩУ ПЫО‡ı m ÒÓ‚Ô‡‰‡ÂÚ Ò Ï‡ÒÒÓÈ ÔÓÍÓfl ˝ÎÂÍÚ Ó- ̇ m0. З ‰ВИТЪ‚ЛЪВО¸МУТЪЛ Н‡К‰˚И ˝ОВНЪ УМ ‚ Н ЛТ- Ъ‡ООВ ‰‚ЛКВЪТfl ‚ ˝ОВНЪ Л˜ВТНУП ФУОВ, ТУБ‰‡‚‡ВПУП ФУОУКЛЪВО¸МУ Б‡ flКВММ˚ПЛ ЛУМ‡ПЛ Н ЛТЪ‡ООЛ˜В- ТНУИ В¯ВЪНЛ Л ‰ Ы„ЛПЛ ˝ОВНЪ УМ‡ПЛ. м ‡‚МВМЛВ ‰‚ЛКВМЛfl ˝ОВНЪ УМ‡ ‚ В‡О¸МУП Н ЛТЪ‡ООВ ЛПВВЪ ‚Л‰
m0a0 = F‚̯ + F‚ÌÚ. |
(6) |
á‰ÂÒ¸ F‚ÌÚ – ТЫПП‡ ТЛО, ТУБ‰‡‚‡ВП˚ı ФУОВП В¯ВЪНЛ Л ‰ Ы„ЛПЛ ˝ОВНЪ УМ‡ПЛ.
ÖÒÎË ·˚ ÒËÎ˚ F‚ÌÚ ·˚ОЛ ЛБ‚ВТЪМ˚, ЪУ ‚˚˜ЛТОВММУВ ФУ ЩУ ПЫОВ (6) ЫТНУ ВМЛВ a0 ÒÓÓÚ‚ÂÚÒÚ‚Ó‚‡ÎÓ ·˚ χÒÒ m0 ÔÓÍÓfl Ò‚Ó·Ó‰ÌÓ„Ó ˝ÎÂÍÚ Ó̇. ä ÒÓʇÎÂ-
Ì˲, F‚ÌÚ ЪУ˜МУ УФ В‰ВОЛЪ¸ МВО¸Бfl, ФУ˝ЪУПЫ Ы‰У·МУ ФУТЪЫФЛЪ¸ ТОВ‰Ы˛˘ЛП У· ‡БУП.
иВ ВМВТВП F‚ÌÚ ЛБ Ф ‡‚УИ ˜‡ТЪЛ Ы ‡‚МВМЛfl ‰‚Л- КВМЛfl (6) ‚ ОВ‚Ы˛. оУ П‡О¸МУ ТОВ‚‡ ‰УОКМУ ТЪУflЪ¸ Ф УЛБ‚В‰ВМЛВ П‡ТТ˚ М‡ ЫТНУ ВМЛfl, ЪУ ВТЪ¸ ПУКМУ Б‡ФЛТ‡Ъ¸
m0a0 –F‚ÌÚ = m*a0.
м ‡‚МВМЛВ ‰‚ЛКВМЛfl ЪВФВ ¸ Ф ЛМЛП‡ВЪ ‚Л‰
m*a0 = F‚̯. |
(7) |
á‰ÂÒ¸ m* – ˝ЪУ Ъ‡Н‡fl П‡ТТ‡, Ф Л НУЪУ УИ Ы˜ВЪ ЪУО¸НУ ‚МВ¯МЛı ТЛО, ‰ВИТЪ‚Ы˛˘Лı М‡ ˝ОВНЪ УМ, ‰‡ВЪ ЛТЪЛММУВ БМ‡˜ВМЛВ ЫТНУ ВМЛfl ˝ОВНЪ УМ‡ ‚ Н ЛТЪ‡ООВ. m* М‡Б˚‚‡ВЪТfl ˝ЩЩВНЪЛ‚МУИ П‡ТТУИ ˝ОВНЪ УМ‡, УФЛТ˚‚‡˛˘ВИ В„У ‰‚ЛКВМЛВ ‚ Н ЛТЪ‡ООВ.
аМЪВ ВТМУ, ˜ЪУ ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡ ПУКВЪ МВ ЪУО¸НУ ТЛО¸МУ УЪОЛ˜‡Ъ¸Тfl УЪ m0 , МУ Л ЛПВЪ¸ УЪ Лˆ‡- ЪВО¸МУВ БМ‡˜ВМЛВ. йЪ Лˆ‡ЪВО¸М‡fl П‡ТТ‡ УБМ‡˜‡ВЪ, ˜ЪУ ˝ОВНЪ УМ ЫТНУ flВЪТfl ‚ М‡Ф ‡‚ОВМЛЛ, Ф УЪЛ‚У- ФУОУКМУП М‡Ф ‡‚ОВМЛ˛ Ф ЛОУКВММУИ ‚МВ¯МВИ ТЛ- О˚. щЪУЪ, Н‡Б‡ОУТ¸ ·˚, М‚ УflЪМ˚И ВБЫО¸Ъ‡Ъ ПУКМУ ОВ„НУ ФУМflЪ¸.
к‡ТТПУЪ ЛП ‰‚ЛКВМЛВ ЪВО‡ ФУ‰ ‰ВИТЪ‚ЛВП ТЛО˚ ЪflКВТЪЛ (F‚̯) ‚ МВНУЪУ УИ Т В‰В. з‡ ˝ЪУ ЪВОУ Н УПВ
70 |
лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹1, 1999 |
ТЛО˚ ЪflКВТЪЛ ‰ВИТЪ‚Ы˛Ъ Ъ‡НКВ ТЛО‡ Ъ ВМЛfl Л ТЛО‡ А ıЛПВ‰‡. йТМУ‚˚‚‡flТ¸ М‡ Ы ‡‚МВМЛЛ (6) ·Ы‰ВП‡ТТП‡Ъ Л‚‡Ъ¸ ‚ВНЪУ МЫ˛ ТЫППЫ ˝ЪЛı ТЛО Н‡Н
F‚ÌÚ = FА ı + FÚ Л ЛТФУО¸БЫВП ‰Оfl УФ В‰ВОВМЛfl m* ÙÓ ÏÛÎÛ (7). ÖÒÎË ÛÒÍÓ ÂÌË Ú· Ì‡Ô ‡‚ÎÂÌÓ ‚ÌËÁ
ÔÓ Ì‡Ô ‡‚ÎÂÌ˲ ÛÒÍÓ ÂÌËfl g, ЪУ ˝ЩЩВНЪЛ‚М‡fl П‡Т- Т‡ ·Ы‰ВЪ ФУОУКЛЪВО¸М‡:
F‚̯
m* = -------------, a0
Ф Л˜ВП, ˜ВП ПВМ¸¯В ЫТНУ ВМЛВ, ЪВП ·УО¸¯В ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡, ˜ЪУ ЩЛБЛ˜ВТНЛ УБМ‡˜‡ВЪ Ы‚ВОЛ˜ВМЛВ ‚МЫЪ ВММЛı ТЛО, Ф ВФflЪТЪ‚Ы˛˘Лı ‰‚ЛКВМЛ˛ ЪВО‡.
З ЪУП КВ ТОЫ˜‡В, НУ„‰‡ ТЛО‡ А ıЛПВ‰‡ Ф В‚˚¯‡- ВЪ ТЛОЫ ЪflКВТЪЛ Л ЫТНУ ВМЛВ ЪВО‡ М‡Ф ‡‚ОВМУ ‚‚В ı Ф УЪЛ‚ М‡Ф ‡‚ОВМЛfl ЫТНУ ВМЛfl g, ЪУ, ˜ЪУ·˚ УФЛ- Т‡Ъ¸ ˝ЪУЪ ВБЫО¸Ъ‡Ъ, ‡ТТП‡Ъ Л‚‡fl ЪУО¸НУ ТЛОЫ ЪflКВТЪЛ, Ф ЛıУ‰ЛЪТfl Т˜ЛЪ‡Ъ¸ ˝ЩЩВНЪЛ‚МЫ˛ П‡ТТЫ ЪВО‡ УЪ Лˆ‡ЪВО¸МУИ (7):
F‚̯
m* = –-------------. a0
нУ˜МУ Ъ‡Н КВ ˜‡ТЪУЪ‡ Ф ВˆВТТЛЛ ω ‚У ‚МВ¯МВП
ÔÓΠB ‚ Í ËÒÚ‡ÎΠÓÔ Â‰ÂÎflÂÚÒfl Ì χÒÒÓÈ ÔÓÍÓfl ˝ÎÂÍÚ Ó̇ m0 , ‡ МВНУЪУ УИ ˝ЩЩВНЪЛ‚МУИ П‡ТТУИ m*, Ы˜ЛЪ˚‚‡˛˘ВИ ‰ВИТЪ‚ЛВ М‡ ˝ОВНЪ УМ ‚МЫЪ ВММЛı ТЛО. лУУЪ‚ВЪТЪ‚ВММУ ‚ПВТЪУ П‡„МВЪУМ‡ ЕУ ‡ ‰Оfl Т‚У·У‰МУ„У ˝ОВНЪ УМ‡ ПУКМУ ‚‚ВТЪЛ ˝ЩЩВНЪЛ‚М˚И П‡„МВЪУМ ЕУ ‡
µe"
* = ---------, 2m*c
„‰Â m*c – ТФЛМУ‚‡fl ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡.
á‡ÏÂ̇ m0 ˝ЩЩВНЪЛ‚МУИ П‡ТТУИ Ф Л‚У‰ЛЪ Н ТПВ- ˘ВМЛ˛ ˝МВ „ВЪЛ˜ВТНЛı Ы У‚МВИ М‡ ЛТ. 2. уВП ПВМ¸¯В ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡, ЪВП ·УО¸¯В Ф Л Б‡‰‡М- МУП Ç ‚ВОЛ˜ЛМ‡ У ·ЛЪ‡О¸МУ„У (Т‚flБ‡ММУ„У Т Ф В- ˆВТТЛВИ ˝ОВНЪ УМ‡) ‡Т˘ВФОВМЛfl Ы У‚МВИ "ω = = "eB/m*, Л ‡М‡ОУ„Л˜МУ, ˜ВП ПВМ¸¯В ТФЛМУ‚‡fl ˝Щ- ЩВНЪЛ‚М‡fl П‡ТТ‡, ЪВП ·УО¸¯В ТФЛМУ‚УВ ‡Т˘ВФОВМЛВ "e B ⁄ m*c .
абеЦзЦзаЦ лЗйвлнЗ ЗЦфЦлнЗД ика дЗДзнйЗДзаа щзЦкЙаа З еДЙзанзйе ийгЦ
䂇МЪУ‚‡МЛВ ˝МВ „ЛЛ ˝ОВНЪ УМУ‚ Ф Л‚У‰ЛЪ Н ‚УБМЛНМУ‚ВМЛ˛ ФВ ЛУ‰Л˜ВТНЛ ‡ТФУОУКВММ˚ı (М‡ ¯Н‡ОВ ˝МВ „ЛЛ) П‡НТЛПЫПУ‚ ‚ ФОУЪМУТЪЛ ˝ОВНЪ УМ- М˚ı ТУТЪУflМЛИ (˜ЛТОВ ˝ОВНЪ УМУ‚, Ф ЛıУ‰fl˘ЛıТfl М‡ В‰ЛМЛ˜М˚И ЛМЪВ ‚‡О ˝МВ „ЛЛ). к‡ТТЪУflМЛВ "ω ПВК‰Ы П‡НТЛПЫП‡ПЛ Ы‚ВОЛ˜Л‚‡ВЪТfl Ф Л Ы‚ВОЛ˜В-
ÌËË ÔÓÎfl B , Ъ‡Н ˜ЪУ Т УТЪУП ФУОfl П‡НТЛПЫП˚ ФВ-ЛУ‰Л˜ВТНЛ ФВ ВТВН‡˛Ъ Ы У‚ВМ¸ оВ ПЛ %F . щЪУ Ф Л‚У‰ЛЪ Н УТˆЛООflˆЛflП ‚ П‡„МЛЪМУП ФУОВ (Ф Л
МЛБНЛı ЪВПФВ ‡ЪЫ ‡ı) ‚ТВı Ф‡ ‡ПВЪ У‚ Н ЛТЪ‡ОО‡, УФ В‰ВОflВП˚ı ˝ОВНЪ УМ‡ПЛ: Ф У‚У‰ЛПУТЪЛ (˝ЩЩВНЪ тЫ·МЛНУ‚‡–‰В Й‡‡Б‡), П‡„МЛЪМУИ ‚УТФ ЛЛП˜Л‚УТЪЛ (˝ЩЩВНЪ ‰В Й‡‡Б‡–‚‡М АО¸ЩВМ‡), ЪВФОУВПНУТЪЛ, ЪВФОУФ У‚У‰МУТЪЛ Л Ъ.‰. е˚ МВ ·Ы‰ВП ‡ТТП‡Ъ Л‚‡Ъ¸ ˝ЪЛ ˝ЩЩВНЪ˚, ‡ У· ‡ЪЛП ‚МЛП‡МЛВ М‡ ЪУ, ˜ЪУ П‡„- МЛЪМУВ ФУОВ ПУКВЪ Ф Л‚У‰ЛЪ¸ Н ТПВ˘ВМЛ˛ „ ‡МЛˆ ˝МВ „ВЪЛ˜ВТНЛı БУМ.
щМВ „ВЪЛ˜ВТНЛИ ТФВНЪ ˝ОВНЪ УМУ‚ ‚ Н ЛТЪ‡ОО‡ı ТУТЪУЛЪ ЛБ ˜В В‰Ы˛˘ЛıТfl ЛМЪВ ‚‡ОУ‚ ‡Б В¯ВММ˚ı Л Б‡Ф В˘ВММ˚ı БМ‡˜ВМЛИ ˝МВ „ЛЛ [4]. з‡ ‰МВ БУМ˚ ˝МВ „Лfl ПЛМЛП‡О¸М‡, Ы ФУЪУОН‡ БУМ˚ П‡НТЛП‡О¸М‡ ( ЛТ. 3).
ᇂЛТЛПУТЪ¸ ˝МВ „ЛЛ УЪ ЛПФЫО¸Т‡ ˝ОВНЪ УМ‡ М‡- Б˚‚‡ВЪТfl Б‡НУМУП ‰ЛТФВ ТЛЛ. З·ОЛБЛ ПЛМЛПЫП‡ ˝МВ „ЛЛ Б‡НУМ ‰ЛТФВ ТЛЛ Н‚‡‰ ‡ЪЛ˜ВМ:
P2
%= ----------. 2m*
è Ë Û‚Â΢ÂÌËË ê ‡ÒÚÂÚ % ( ËÒ. 3, ‡). лОВ‰У‚‡ЪВО¸- МУ, ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡ m* > 0.
З·ОЛБЛ П‡НТЛПЫП‡ ˝МВ „ЛЛ Ф Л Ы‚ВОЛ˜ВМЛЛ % ЛПФЫО¸Т ˝ОВНЪ УМ‡, УЪТ˜ЛЪ‡ММ˚И УЪ ЪУ˜НЛ, ‚ НУЪУ-УИ ˝МВ „Лfl П‡НТЛП‡О¸М‡, ЫПВМ¸¯‡ВЪТfl. щЪУ УБМ‡- ˜‡ВЪ, ˜ЪУ Ы ˝ОВНЪ УМУ‚, Б‡МЛП‡˛˘Лı ˝МВ „ВЪЛ˜ВТНЛВ ТУТЪУflМЛfl ‚·ОЛБЛ ФУЪУОН‡ БУМ˚, ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡ m* < 0. йЪ Лˆ‡ЪВО¸МУВ БМ‡˜ВМЛВ ˝ЩЩВНЪЛ‚- МУИ П‡ТТ˚ Ф Л‚У‰ЛЪ Н УЪ Лˆ‡ЪВО¸МУПЫ БМ‡˜ВМЛ˛ ‚ВОЛ˜ЛМ˚ "ω. щЪУ УБМ‡˜‡ВЪ, ˜ЪУ ˝ОВНЪ УМ Ы ФУЪУОН‡ БУМ˚ Ф ВˆВТТЛ ЫВЪ ‚ ФУОВ ‚ М‡Ф ‡‚ОВМЛЛ, У· ‡ЪМУП
% ‡
0 P4 P3
%4 |
P |
%3
%2 %1
0 P1P2 |
P |
% |
· |
|
|
0 |
|
|
n = 0 |
|
n = 1 |
|
n = 2 |
|
B ± 0 |
êËÒ. 3. ᇂЛТЛПУТЪ¸ ˝МВ „ЛЛ УЪ ЛПФЫО¸Т‡ ‚·ОЛБЛ ВВ ˝НТЪ ВП‡О¸М˚ı БМ‡˜ВМЛИ ‚ ˝МВ „ВЪЛ˜ВТНУИ БУМВ. аПФЫО¸Т УЪТ˜ЛЪ˚‚‡ВЪТfl УЪ ЪУ˜ВН ˝НТЪ ВПЫПУ‚:
‡ – Ç = 0. á̇˜ÂÌËflÏ ˝Ì „ËË %1 < %2 Ы ‰М‡ БУМ˚ ТУУЪ‚ВЪТЪ‚Ы˛Ъ ЛПФЫО¸Т˚ ê1 < P2 . м ФУЪУОН‡ БУМ˚ Ф Л Ы‚ВОЛ˜ВМЛЛ ˝МВ „ЛЛ (%3 < %4) ЛПФЫО¸Т ˝ОВН- Ъ УМ‡ ЫПВМ¸¯‡ВЪТfl (ê3 > P4); · – Ç 0. лıВП‡ ˝МВ „ВЪЛ˜ВТНЛı Ы У‚МВИ ‚·ОЛБЛ ФУЪУОН‡ БУМ˚. зЫПВ ‡ˆЛfl Ы У‚МВИ Л‰ВЪ Т‚В ıЫ ‚МЛБ, Ъ‡Н ˜ЪУ ФУЪУОУН БУМ˚ ‚ П‡„МЛЪМУП ФУОВ УФ В‰ВОflВЪТfl ФУОУКВМЛВП Ы У‚Мfl n = 0 Т У ЛВМЪ‡ˆЛВИ ТФЛМ‡, М‡Ф ‡‚- ОВММУИ ‚МЛБ (БВОВМ‡fl ТЪ ВОН‡)
ЕкДзСн з.Е. оДбйЗхЦ иЦкЦпйСх З еДЙзанзйе ийгЦ |
71 |
М‡Ф ‡‚ОВМЛ˛ Ф ВˆВТТЛЛ Ы ‰М‡ БУМ˚. иУ˝ЪУПЫ ВТОЛ УЪТ˜ЛЪ˚‚‡Ъ¸ ˝МВ „Л˛ УЪ ВВ П‡НТЛП‡О¸МУ„У БМ‡˜В- МЛfl ‚ БУМВ, ЪУ МЫПВ ‡ˆЛfl ‚УБМЛН‡˛˘Лı ‚ П‡„МЛЪМУП ФУОВ Ы У‚МВИ %n ·Ы‰ВЪ Л‰ЪЛ УЪ ФУЪУОН‡ БУМ˚ ‚МЛБ ( ЛТ. 3, ·).
иЫТЪ¸ БУМ‡ ˜‡ТЪЛ˜МУ Б‡ФУОМВМ‡ ˝ОВНЪ УМ‡ПЛ. ЕЫ‰ВП УЪТ˜ЛЪ˚‚‡Ъ¸ ˝МВ „Л˛ УЪ ВВ БМ‡˜ВМЛfl М‡ ‰МВ БУМ˚ Ф Л Ç = 0. ЗЛ‰МУ ( ЛТ. 2), ˜ЪУ ‚ П‡„МЛЪМУП ФУОВ БМ‡˜ВМЛВ ПЛМЛП‡О¸МУИ ˝МВ „ЛЛ (ФУОУКВМЛВ ‰М‡ БУМ˚) УФ В‰ВОflВЪТfl ‡БМУТЪ¸˛
"ω |
– |
|
c B |
|
= |
e" |
1 |
– |
1 |
|
(8) |
------- |
|
|
------ --- |
--- |
--- |
B. |
|||||
2 |
|
|
|
|
|
2 m* |
mc* |
|
|||
ÖÒÎË m* < m*c , ÚÓ ‰ÌÓ ÁÓÌ˚ ÔÓ‰ÌËχÂÚÒfl ‚ ÔÓÎÂ, ÂÒÎË, Ì‡Ó·Ó ÓÚ, m* > m*c , ЪУ ‰МУ БУМ˚ ·Ы‰ВЪ ТПВ- ˘‡Ъ¸Тfl ‚МЛБ (ФУ ˝МВ „ЛЛ) ‚ П‡„МЛЪМУП ФУОВ.
иУОУКВМЛВ ФУЪУОН‡ БУМ˚ ‚ ФУОВ УФ В‰ВОflВЪТfl‡БМУТЪ¸˛
|
"ω |
|
c B |
|
= e" |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||||||||
– |
+ |
|
-– |
|
+ |
B. |
(9) |
|||||
|
2 |
|
|
|
2 |
|
m* |
|
| mc* | |
|
||
|
|
|
|
|
|
|
||||||
è Ë m* < m*c ФУЪУОУН БУМ˚ УФЫТН‡ВЪТfl ‚МЛБ, Ф Л m* > m*c , Ì‡Ó·Ó ÓÚ, ÔÓ‰ÌËχÂÚÒfl ‚‚ ı.
еЦнДггх, ийгмикйЗйСзада, СащгЦднкада
иУ УФ В‰ВОВМЛ˛, Н ПВЪ‡ОО‡П УЪМУТflЪТfl Ф У‚У‰- МЛНЛ ˝ОВНЪ Л˜ВТНУ„У ЪУН‡, Ы НУЪУ ˚ı НУМˆВМЪ ‡ˆЛfl НУООВНЪЛ‚ЛБЛ У‚‡ММ˚ı ˝ОВНЪ УМУ‚ МВ Б‡‚ЛТЛЪ УЪ ЪВПФВ ‡ЪЫ ˚ ‚У ‚ТВП ЛМЪВ ‚‡ОВ ЪВПФВ ‡ЪЫ УЪ í = = 0 д ‰У ЪУ˜НЛ ФО‡‚ОВМЛfl. м ФУОЫФ У‚У‰МЛНУ‚ НУМˆВМЪ ‡ˆЛfl МУТЛЪВОВИ ЪУН‡ ЫПВМ¸¯‡ВЪТfl Ф Л ФУМЛКВМЛЛ ЪВПФВ ‡ЪЫ ˚ Л Ф Л í = 0 д У· ‡˘‡ВЪТfl ‚ МЫО¸. м ‰Л˝ОВНЪ ЛНУ‚ ˝ОВНЪ УММ‡fl Ф У‚У‰ЛПУТЪ¸ Ф ‡Н- ЪЛ˜ВТНЛ УЪТЫЪТЪ‚ЫВЪ ‚У ‚ТВИ У·О‡ТЪЛ ЪВПФВ ‡ЪЫ .
мН‡Б‡ММУВ ‡БОЛ˜ЛВ УФ В‰ВОflВЪТfl ‡БОЛ˜ЛВП ‚ ТЪ ЫНЪЫ В ˝МВ „ВЪЛ˜ВТНУ„У ТФВНЪ ‡ Н ЛТЪ‡ООУ‚. щМВ „ВЪЛ˜ВТНЛИ ТФВНЪ “У‰МУПВ МУ„У” ПВЪ‡ОО‡, ТУТЪУfl˘В„У ЛБ ˆВФУ˜НЛ ‡ЪУПУ‚, ТУТЪУЛЪ ЛБ fl‰‡ ˝МВ „ВЪЛ˜ВТНЛı БУМ, ‡Б‰ВОВММ˚ı Ф УПВКЫЪН‡ПЛ Б‡Ф В˘ВММ˚ı БМ‡˜ВМЛИ ˝МВ „ЛЛ ЛОЛ, Н‡Н Ф ЛМflЪУ „У‚У ЛЪ¸, ˝МВ „ВЪЛ˜ВТНЛПЛ ˘ВОflПЛ [4]. З “У‰МУПВ МУП” ТОЫ˜‡В БУМ˚ МВ ФВ ВН ˚‚‡˛ЪТfl. иУТНУО¸- НЫ ˜ЛТОУ ПВТЪ ‚ БУМВ ‡‚МУ 2N (N – ˜ЛТОУ ‡ЪУПУ‚ ‚ ˆВФУ˜НВ) [4], ЪУ Ы У‰МУ‚‡ОВМЪМ˚ı ПВЪ‡ООУ‚ ФВ ‚‡fl БУМ‡ Б‡ФУОМВМ‡ М‡ФУОУ‚ЛМЫ, Ы Ъ Вı‚‡ОВМЪМ˚ı ФВ - ‚‡fl Б‡ФУОМВМ‡ ФУОМУТЪ¸˛, ‡ ‚ЪУ ‡fl – ЪУО¸НУ М‡ФУОУ‚ЛМЫ. щЪУ БМ‡˜ЛЪ, ˜ЪУ У‰МУПВ М˚В Н ЛТЪ‡ОО˚, У·-‡БУ‚‡ММ˚В ‡ЪУП‡ПЛ МВ˜ВЪМУИ ‚‡ОВМЪМУТЪЛ, ‚ТВ„‰‡ ПВЪ‡ОО˚. и Л ˜ВЪМУИ ‚‡ОВМЪМУТЪЛ У‰М‡ ЛОЛ ‰‚В БУ- М˚ Б‡ФУОМВМ˚ ФУОМУТЪ¸˛ ˝ОВНЪ УМ‡ПЛ, ‡ ‡ТФУОУКВММ‡fl ‚˚¯В БУМ‡ ФЫТЪ‡. ЦТОЛ ˝МВ „ВЪЛ˜ВТН‡fl ˘ВО¸ ПВК‰Ы МЛПЛ ‚ВОЛН‡, ЪУ ‚В˘ВТЪ‚У – ‰Л˝ОВНЪ ЛН. ЦТОЛ ˘ВО¸ П‡О‡, ЪУ ˝ОВНЪ УМ˚ ЛБ Б‡ФУОМВММУИ БУМ˚ ФУ‰ ‰ВИТЪ‚ЛВП ЪВФОУ‚УИ ˝МВ „ЛЛ kí (k – НУМТЪ‡МЪ‡ ЕУО¸ˆП‡М‡) ФВ В· ‡Т˚‚‡˛ЪТfl ‚ ‚В ıМ˛˛ ФЫТЪЫ˛ БУМЫ, ‚ ВБЫО¸Ъ‡ЪВ ˜В„У ‚ ‚В ıМВИ БУМВ ФУfl‚Оfl˛ЪТfl
˝ОВНЪ УМ˚ Ф У‚У‰ЛПУТЪЛ, ‡ ‚ МЛКМВИ БУМВ – Ы ВВ ФУЪУОН‡ МВБ‡ФУОМВММ˚В ТУТЪУflМЛfl. и Л í  0 НУМˆВМЪ ‡ˆЛfl ЪВ ПЛ˜ВТНЛ ‚УБ·ЫК‰ВММ˚ı МУТЛЪВОВИ ЪУН‡ У· ‡˘‡ВЪТfl ‚ МЫО¸. н‡НЛВ ‚В˘ВТЪ‚‡ fl‚Оfl˛Ъ- Тfl ФУОЫФ У‚У‰МЛН‡ПЛ.
0 НУМˆВМЪ ‡ˆЛfl ЪВ ПЛ˜ВТНЛ ‚УБ·ЫК‰ВММ˚ı МУТЛЪВОВИ ЪУН‡ У· ‡˘‡ВЪТfl ‚ МЫО¸. н‡НЛВ ‚В˘ВТЪ‚‡ fl‚Оfl˛Ъ- Тfl ФУОЫФ У‚У‰МЛН‡ПЛ.
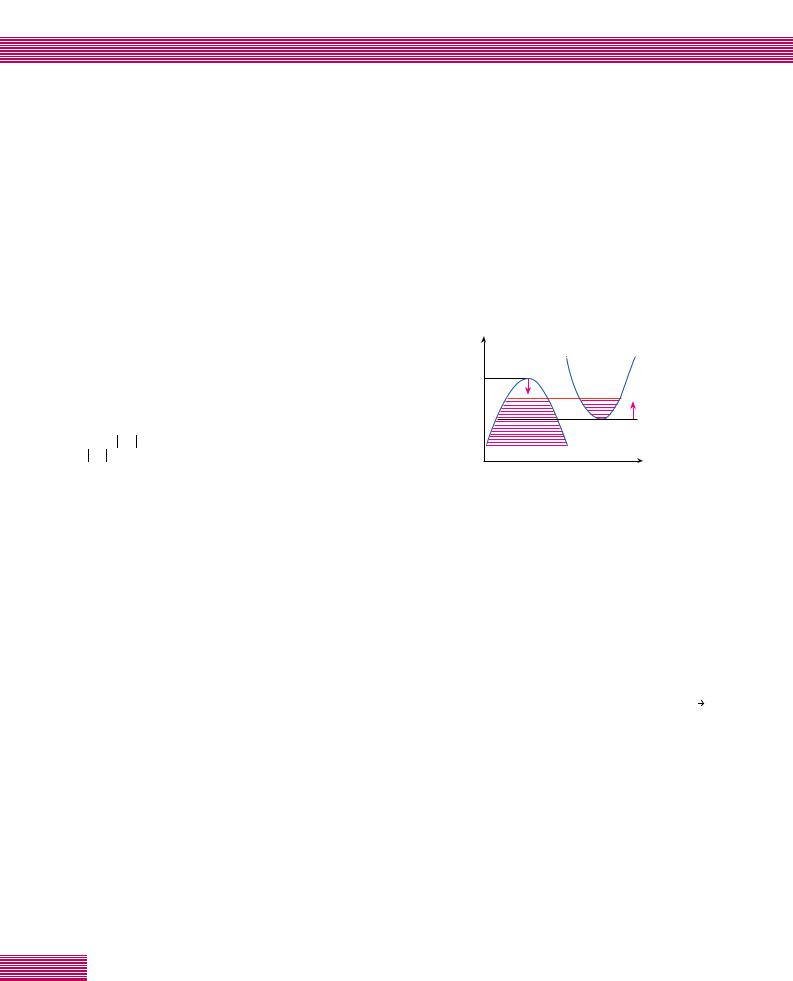
м В‡О¸М˚ı ‰‚ЫıЛОЛ Ъ ВıПВ М˚ı Н ЛТЪ‡ООУ‚ ‚ВБЫО¸Ъ‡ЪВ ‡МЛБУЪ УФЛЛ БУМ˚ ПУ„ЫЪ ФВ ВН ˚‚‡Ъ¸Тfl, ЪУ ВТЪ¸ ФУЪУОУН МЛКМВИ БУМ˚ ПУКВЪ ‡ТФУО‡„‡Ъ¸Тfl ‚˚¯В ‰М‡ ТОВ‰Ы˛˘ВИ БУМ˚. З ˝ЪУП ТОЫ˜‡В Н ЛТЪ‡О- О˚, У· ‡БУ‚‡ММ˚В ‰‚Ыı‚‡ОВМЪМ˚ПЛ ‡ЪУП‡ПЛ, ·Ы‰ЫЪ У·О‡‰‡Ъ¸ ПВЪ‡ООЛ˜ВТНУИ Ф У‚У‰ЛПУТЪ¸˛ ‚ ВБЫО¸Ъ‡- ЪВ ЪУ„У, ˜ЪУ ˜‡ТЪ¸ ˝ОВНЪ УМУ‚ ЛБ ФУОМУТЪ¸˛ Б‡ФУОМВММУИ МЛКМВИ БУМ˚ ФВ ВЪВ˜ВЪ ‚ ФЫТЪЫ˛ БУМЫ, Т НУЪУ УИ УМ‡ ФВ ВН ˚‚‡ВЪТfl ( ЛТ. 4).
% |
|
|
%1 |
I |
II |
%F |
|
|
%2 |
|
|
0 |
|
P |
êËÒ. 4. иУОУКВМЛВ Ы У‚Мfl оВ ПЛ %F Ы ‰‚Ыı‚‡- ОВМЪМУ„У ПВЪ‡ОО‡ Т ФВ ВН ˚‚‡˛˘ЛПЛТfl ˝МВ „В- ЪЛ˜ВТНЛПЛ БУМ‡ПЛ. %1 – ФУОУКВМЛВ ФУЪУОН‡ БУМ˚ I; %2 – ФУОУКВМЛВ ‰М‡ БУМ˚ II. у‡ТЪ¸ ˝ОВНЪ УМУ‚ ЛБ БУМ˚ I ФВ ВЪВНО‡ ‚ БУМЫ II
оДбйЗхЦ иЦкЦпйСх еЦнДгг–СащгЦднкад а СащгЦднкад–еЦнДгг З еДЙзанзйе ийгЦ
З˚·В ВП ‚ Н‡˜ВТЪ‚В У·˙ВНЪ‡ ЛТТОВ‰У‚‡МЛfl ПВ- Ъ‡ОО, Ы НУЪУ У„У ‰‚В ТУТВ‰МЛВ БУМ˚ ФВ ВН ˚‚‡˛ЪТfl Л ˜ЛТОУ Б‡ФУОМВММ˚ı ТУТЪУflМЛИ ‚ ‚В ıМВИ БУМВ ‡‚- МУ ˜ЛТОЫ ФЫТЪ˚ı ПВТЪ ‚ МЛКМВИ ( ЛТ. 4).
иЫТЪ¸ ТУУЪМУ¯ВМЛВ ˝ЩЩВНЪЛ‚М˚ı П‡ТТ m* Ë m*c
Ъ‡НУ‚У, ˜ЪУ ФУЪУОУН МЛКМВИ БУМ˚ %1 УФЫТН‡ВЪТfl ‚ B (Í ‡Ò̇fl ÒÚ ÂÎ͇), ‡ ‰ÌÓ ‚ ıÌÂÈ ÁÓÌ˚ %2 ФУ‰МЛП‡- ВЪТfl. нУ„‰‡ ‚ П‡„МЛЪМУП ФУОВ ‚ВОЛ˜ЛМ‡ ФВ ВН ˚ЪЛfl БУМ %1 − %2 ЫПВМ¸¯‡ВЪТfl Л Ф Л УФ В‰ВОВММУП Н ЛЪЛ- ˜ВТНУП БМ‡˜ВМЛЛ ФУОfl BÍ У· ‡ЪЛЪТfl ‚ МЫО¸. и Л ‰‡О¸МВИ¯ВП Ы‚ВОЛ˜ВМЛЛ ФУОfl ПВК‰Ы БУМ‡ПЛ У· ‡- БЫВЪТfl ˝МВ „ВЪЛ˜ВТН‡fl ˘ВО¸, Ы‚ВОЛ˜Л‚‡˛˘‡flТfl Т Ç. З ВБЫО¸Ъ‡ЪВ ˝ЪУ„У НУМˆВМЪ ‡ˆЛfl МУТЛЪВОВИ ЪУН‡ (Ф Л МЛБНЛı ЪВПФВ ‡ЪЫ ‡ı) ·Ы‰ВЪ ·˚ТЪ У ЫПВМ¸- ¯‡Ъ¸Тfl Л ‚ ‰УТЪ‡ЪУ˜МУ ТЛО¸МУП ФУОВ У· ‡ЪЛЪТfl ‚ МЫО¸. щЪУ БМ‡˜ЛЪ, ˜ЪУ Ф Л Ç = ÇÍ Ф УЛТıУ‰ЛЪ ФВ ВıУ‰ ЛБ ПВЪ‡ООЛ˜ВТНУ„У, ТМ‡˜‡О‡ ‚ ФУОЫФ У‚У‰МЛНУ‚УВ, ‡ Б‡ЪВП ‰Л˝ОВНЪ Л˜ВТНУВ ТУТЪУflМЛВ. и Л˜ВП ˝ЪУЪ ФВ-ВıУ‰ МВ ТУФ У‚УК‰‡ВЪТfl ЛБПВМВМЛВП ТЪ ЫНЪЫ ˚ Н ЛТЪ‡ООЛ˜ВТНУИ В¯ВЪНЛ Л ФУОМУТЪ¸˛ У· ‡ЪЛП Ф Л ЛБПВМВМЛЛ ‚ВОЛ˜ЛМ˚ ФУОfl.
72 |
лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹1, 1999 |

к‡ТТПУЪ ЛП ЪВФВ ¸ ‰Л˝ОВНЪ ЛН (ЛОЛ ФУОЫФ У- ‚У‰МЛН), Ы НУЪУ У„У Ф Л Ç = 0 МЛКМflfl БУМ‡ ФУОМУТЪ¸˛ Б‡ФУОМВМ‡ ˝ОВНЪ УМ‡ПЛ, ‡ ТОВ‰Ы˛˘‡fl, УЪ‰В- ОВММ‡fl ˝МВ „ВЪЛ˜ВТНУИ ˘ВО¸˛ ФЫТЪ‡. иЫТЪ¸ ‚ П‡„МЛЪМУП ФУОВ ФУЪУОУН МЛКМВИ БУМ˚ ФУ‰МЛП‡ВЪТfl, ‡ ‰МУ МЛКМВИ УФЫТН‡ВЪТfl. нУ„‰‡ Ф Л ФУОВ Ç = ÇÍ ˝Ì „ÂÚ˘ÂÒ͇fl ˘Âθ Ó· ‡ÚËÚÒfl ‚ ÌÛθ Ë Ô Ë ‰‡Î¸- ÌÂȯÂÏ ÓÒÚÂ Ç ‚УБМЛНМВЪ ФВ ВН ˚ЪЛВ БУМ Т ФУfl‚- ОВМЛВП ˝ОВНЪ УМУ‚ Ф У‚У‰ЛПУТЪЛ ‚ ‚В ıМВИ БУМВ Л ФЫТЪ˚ı ПВТЪ ‚ МЛКМВИ. З ˝ЪУП ТОЫ˜‡В Ф Л Ç = ÇÍ Ф У- ЛТıУ‰ЛЪ Щ‡БУ‚˚И ФВ ВıУ‰ ЛБ ‰Л˝ОВНЪ Л˜ВТНУ„У ‚ ПВЪ‡ООЛ˜ВТНУВ ТУТЪУflМЛВ, ТУФ У‚УК‰‡˛˘ЛИТfl ВБНЛП Ы‚ВОЛ˜ВМЛВП ˝ОВНЪ УФ У‚У‰МУТЪЛ.
ЕЦлфЦгЦЗйЦ лйлнйьзаЦ
З˚¯В ‡ТТП‡Ъ Л‚‡О‡Т¸ ТЛЪЫ‡ˆЛfl, НУ„‰‡ П‡НТЛПЫП˚ Л ПЛМЛПЫП˚ ˝МВ „ЛЛ ‚ БУМ‡ı ‡ТФУОУКВМ˚ Ф Л ‡БОЛ˜М˚ı БМ‡˜ВМЛflı ЛПФЫО¸Т‡ ( ЛТ. 4). й‰М‡- НУ ‚ МВНУЪУ ˚ı ТОЫ˜‡flı (Н‡Н, М‡Ф ЛПВ , Ы МВНУЪУ-˚ı ФУОЫФ У‚У‰МЛНУ‚ [4]) П‡НТЛПЫП МЛКМВИ БУМ˚ Л ПЛМЛПЫП ˝МВ „ЛЛ ‚ ‚В ıМВИ ‡ТФУОУКВМ˚ ‰ Ы„ М‡‰ ‰ Ы„УП Ф Л У‰МУП Л ЪУП КВ БМ‡˜ВМЛЛ ЛПФЫО¸Т‡.
уЪУ ·Ы‰ВЪ, ВТОЛ УМЛ ТПВ˘‡˛ЪТfl ‚ П‡„МЛЪМУП ФУОВ М‡‚ТЪ В˜Ы ‰ Ы„ ‰ Ы„Ы? щЪУЪ ТОЫ˜‡И УТУ·ВММУ ЛМЪВ ВТВМ, Ъ‡Н Н‡Н ФУ Б‡НУМ‡П Н‚‡МЪУ‚УИ ПВı‡МЛНЛ БУ- М˚ МВ ПУ„ЫЪ ‚УИЪЛ У‰М‡ ‚ ‰ Ы„Ы˛. иУ˝ЪУПЫ БУМ˚ ФВ ВПВ˘‡˛ЪТfl МВБ‡‚ЛТЛПУ ОЛ¯¸ ‰У ЪВı ФУ , ФУН‡ ˝МВ „ВЪЛ˜ВТН‡fl ˘ВО¸ ПВК‰Ы МЛПЛ МВ У· ‡ЪЛЪТfl ‚ МЫО¸. б‡ЪВП БУМ˚ Н‡Н ·˚ УЪ ‡К‡˛ЪТfl ‰ Ы„ УЪ ‰ Ы„‡ Л Ф Л Ы‚ВОЛ˜ВМЛЛ ФУОfl М‡˜ЛМ‡˛Ъ ‡ТıУ‰ЛЪ¸Тfl, Ъ‡Н ˜ЪУ ˘ВО¸ ПВК‰Ы МЛПЛ Ы‚ВОЛ˜Л‚‡ВЪТfl. и Л УФ В‰В- ОВММУП БМ‡˜ВМЛЛ ФУОfl ÇÍ, НУ„‰‡ БУМ˚ ТУ¯ОЛТ¸, У·-‡БЫВЪТfl МУ‚УВ, МВ ТЫ˘ВТЪ‚Ы˛˘ВВ ‚ У·˚˜М˚ı ЫТОУ‚Л- flı ТУТЪУflМЛВ ‚В˘ВТЪ‚‡, НУЪУ УВ ФУОЫ˜ЛОУ М‡Б‚‡МЛВ ·ВТ˘ВОВ‚У„У. З ˝ЪУП ТУТЪУflМЛЛ ‚В˘ВТЪ‚У МВ fl‚ОflВЪТfl МЛ ФУОЫФ У‚У‰МЛНУП, МЛ ПВЪ‡ООУП Л У·О‡‰‡ВЪ ТУ‚В ¯ВММУ МВУ·˚˜М˚ПЛ Т‚УИТЪ‚‡ПЛ.
дДд Ехга йндкхнх оДбйЗхЦ иЦкЦпйСх З еДЙзанзйе ийгЦ
уЪУ·˚ У·М‡ ЫКЛЪ¸ Щ‡БУ‚˚В ФВ ВıУ‰˚ ‚ П‡„МЛЪМУП ФУОВ, Ф Л¯ОУТ¸ М‡ИЪЛ В¯ВМЛВ fl‰‡ Ф У·ОВП. и ВК‰В ‚ТВ„У ˝ЪУ ‚˚·У М‡Л·УОВВ Ы‰У·МУ„У У·˙ВНЪ‡ ЛТТОВ‰У‚‡МЛИ. з‡‰У ·˚ОУ М‡ИЪЛ Ъ‡НУВ ‚В˘ВТЪ‚У, Ы НУЪУ У„У, ‚У-ФВ ‚˚ı, ФВ ВН ˚ЪЛВ БУМ (‰Оfl ПВЪ‡О- ОУ‚) ЛОЛ ˝МВ „ВЪЛ˜ВТН‡fl ˘ВО¸ (‰Оfl ФУОЫФ У‚У‰МЛНУ‚) Ф Л Ç = 0 ·˚ОЛ ·˚ ‰УТЪ‡ЪУ˜М˚ П‡О˚, ˜ЪУ·˚ ФВ-ВıУ‰˚ ПУКМУ ·˚ОУ М‡·О˛‰‡Ъ¸ ‚ ‰УТЪЛКЛП˚ı П‡„МЛЪМ˚ı ФУОflı. ЗУ-‚ЪУ ˚ı, Ы ЛТТОВ‰ЫВПУ„У ‚В˘В- ТЪ‚‡ ˝ЩЩВНЪЛ‚М˚В П‡ТТ˚ У ·ЛЪ‡О¸МУ„У ‰‚ЛКВМЛfl ˝ОВНЪ УМУ‚ m* Л ТФЛМУ‚‡fl m*c ‰ÓÎÊÌ˚ ÒÛ˘ÂÒÚ‚ÂÌÌÓ‡Á΢‡Ú¸Òfl. ÑÎfl Ò‚Ó·Ó‰Ì˚ı ˝ÎÂÍÚ ÓÌÓ‚, ÍÓÚÓ ˚ ‰Ó ˝ÚÓ„Ó ‡ÒÒÏ‡Ú Ë‚‡ÎËÒ¸ ‚ ÚÂÓ ÂÚ˘ÂÒÍËı ‡·ÓÚ‡ı, m* = m*c = m0, Ъ‡Н ˜ЪУ „ ‡МЛˆ˚ БУМ ‚УУ·˘В МВ ТПВ- ˘‡˛ЪТfl ‚ ФУОВ. ЗУФ УТ У ТУУЪМУ¯ВМЛЛ П‡ТТ m* Ë m*c ‚ ЪУ ‚ ВПfl ·˚О Ф ‡НЪЛ˜ВТНЛ МВ ЛТТОВ‰У‚‡М. З-Ъ ВЪ¸Лı, ‚В˘ВТЪ‚У ‰УОКМУ ·˚Ъ¸ ПУМУН ЛТЪ‡ООУП.
С Ы„‡fl Ф У·ОВП‡ ПВЪУ‰Л˜ВТН‡fl. зЫКМУ ·˚ОУ ЛПВЪ¸ ‚УБПУКМУТЪ¸ Ф У‚У‰ЛЪ¸ ЛТТОВ‰У‚‡МЛfl Ф Л МЛБНЛı ЪВПФВ ‡ЪЫ ‡ı, ‚·ОЛБЛ ‡·ТУО˛ЪМУ„У МЫОfl, ˜ЪУ·˚ П‡НТЛП‡О¸МУ ЫПВМ¸¯ЛЪ¸ ˝ЩЩВНЪ ЪВ ПЛ˜ВТНУ„У ФВ В· УТ‡ МУТЛЪВОВИ ЪУН‡ ˜В ВБ ˘ВО¸, ˜ЪУ ФУБ- ‚УОЛОУ ·˚ М‡·О˛‰‡Ъ¸ ФВ ВıУ‰˚ М‡Л·УОВВ УЪ˜ВЪОЛ- ‚У, ‚ ЫБНУП ЛМЪВ ‚‡ОВ П‡„МЛЪМ˚ı ФУОВИ. СОfl ˝ЪУИ ˆВОЛ М‡‰У ·˚ОУ ТУБ‰‡Ъ¸ ЫТЪ‡МУ‚НЫ, ФУБ‚УОfl˛˘Ы˛ ФУОЫ˜‡Ъ¸ Ф В‰ВО¸МУ ТЛО¸М˚В П‡„МЛЪМ˚В ФУОfl, Л ЛПВЪ¸ ‚УБПУКМУТЪ¸ ЛБПВ flЪ¸ ˝ОВНЪ Л˜ВТНУВ ТУФ У- ЪЛ‚ОВМЛВ У· ‡БˆУ‚ Н‡Н ЩЫМНˆЛ˛ П‡„МЛЪМУ„У ФУОfl. иУОЫ˜‡Ъ¸ ТЛО¸М˚В П‡„МЛЪМ˚В ФУОfl ПУКМУ ЪУО¸НУ ‚ ‚Л‰В НУ УЪНЛı ЛПФЫО¸ТУ‚ [6], Л ФУ˝ЪУПЫ Ф У‚В‰ВМЛВ ЛБПВ ВМЛИ ‚ Ъ‡НЛı ЫТОУ‚Лflı, Н ЪУПЫ КВ Ф Л У˜ВМ¸ МЛБНЛı ЪВПФВ ‡ЪЫ ‡ı, Т‡ПУ ФУ ТВ·В ‰УТЪ‡ЪУ˜МУ ТОУКМ‡fl Б‡‰‡˜‡. д УПВ ЪУ„У, М‡‰У ·˚ОУ ЛПВЪ¸ ‚ ‚Л- ‰Ы, ˜ЪУ ВТОЛ У· ‡БВˆ У·О‡‰‡ВЪ ‚˚ТУНУИ ˝ОВНЪ УФ У- ‚У‰МУТЪ¸˛ σ, ЪУ ЪУО˘ЛМ‡ ТНЛМ-ТОУfl
1 |
|
–-- |
|
δ (νσ) 2 |
(10) |
(ФУ‚В ıМУТЪМУ„У ТОУfl, ‚ НУЪУ ˚И Ф УМЛН‡ВЪ ФВ В- ПВММУВ ˝ОВНЪ УП‡„МЛЪМУВ ФУОВ Т ˜‡ТЪУЪУИ ν), Ф Л НУ УЪНУП ЛПФЫО¸ТВ ФУОfl УН‡Б˚‚‡ВЪТfl ПВМ¸¯В ‡Б- ПВ У‚ У· ‡Бˆ‡. З ВБЫО¸Ъ‡ЪВ Ф УМЛН‡˛˘ВВ ‚ У· ‡БВˆ П‡„МЛЪМУВ ФУОВ УН‡Б˚‚‡ВЪТfl ТЛО¸МУ МВУ‰МУ У‰М˚П.
аБ ˜ЛТЪ˚ı ˝ОВПВМЪУ‚ ЫН‡Б‡ММ˚П ‚˚¯В Ъ В·У‚‡- МЛflП Ы‰У‚ОВЪ‚У fl˛Ъ ФУОЫПВЪ‡ОО˚ Bi, Sb, As, „ ‡- ЩЛЪ. аБ МЛı ПЛМЛП‡О¸МЫ˛ ‚ВОЛ˜ЛМЫ ФВ ВН ˚ЪЛfl БУМ ЛПВВЪ Bi. аТФУО¸БЫfl ЛБ‚ВТЪМ˚В ‰‡ММ˚В У· ˝Щ- ЩВНЪЛ‚М˚ı П‡ТТ‡ı m* Ë m*c Ы Bi, ПУКМУ ·˚ОУ УˆВМЛЪ¸ ‚ВОЛ˜ЛМЫ ФУОfl ÇÍ , Ф Л НУЪУ УП Bi ‰УОКВМ Ф В- ‚ ‡ЪЛЪ¸Тfl ‚ ‰Л˝ОВНЪ ЛН. йН‡Б‡ОУТ¸, ˜ЪУ БМ‡˜ВМЛВ ÇÍ ТУТЪ‡‚ОflВЪ 100 нО. д ТУК‡ОВМЛ˛, ФУОfl Ъ‡НУИ ‚ВОЛ- ˜ЛМ˚ ‚ ЪУ ‚ ВПfl ФУОЫ˜ЛЪ¸ ·˚ОУ МВО¸Бfl. нУ„‰‡ ‚УБМЛН- О‡ Л‰Вfl УЪН‡Б‡Ъ¸Тfl УЪ ЛТТОВ‰У‚‡МЛfl ˝ОВПВМЪ‡ М˚ı ПВЪ‡ООУ‚ Л ФУФ˚Ъ‡Ъ¸Тfl М‡ИЪЛ ФУОЫПВЪ‡ООЛ˜ВТНЛВ ТФО‡‚˚, Ы НУЪУ ˚ı ‚ВОЛ˜ЛМ‡ ФВ ВН ˚ЪЛfl ПВМ¸¯В, ˜ВП Ы Bi. д Ъ‡НЛП ТФО‡‚‡П УЪМУТflЪТfl, ‚ ˜‡ТЪМУТЪЛ, Ъ‚В ‰˚В ‡ТЪ‚У ˚ Sb ‚ Bi. и Л Ы‚ВОЛ˜ВМЛЛ НУМˆВМ- Ъ ‡ˆЛЛ Sb ФВ ВН ˚ЪЛВ БУМ Ы Bi ЫПВМ¸¯‡ВЪТfl, ‡ ‡Б- ОЛ˜ЛВ БМ‡˜ВМЛИ m* Ë m*c ÒÓı ‡ÌflÂÚÒfl.
и Л ·УО¸¯Лı НУМˆВМЪ ‡ˆЛflı Sb ТФО‡‚˚ ФВ ВıУ- ‰flЪ ‚ ФУОЫФ У‚У‰МЛНУ‚УВ ТУТЪУflМЛВ, Ф Л˜ВП, ЛБПВМflfl НУМˆВМЪ ‡ˆЛ˛ Sb, ПУКМУ ‚‡ ¸Л У‚‡Ъ¸ ‚ВОЛ˜Л- МЫ ˝МВ „ВЪЛ˜ВТНУИ ˘ВОЛ. а М‡НУМВˆ, УН‡Б‡ОУТ¸, ˜ЪУ ТУУЪМУ¯ВМЛВ П‡ТТ m* Ë m*c Ы ТФО‡‚У‚ Bi–Sb Б‡‚ЛТЛЪ УЪ У ЛВМЪ‡ˆЛЛ П‡„МЛЪМУ„У ФУОfl УЪМУТЛЪВО¸МУ Н Л- ТЪ‡ООУ„ ‡ЩЛ˜ВТНЛı УТВИ Н ЛТЪ‡ОО‡, ˜ЪУ ‰‡ВЪ ‚УБПУКМУТЪ¸, ЛБПВМflfl У ЛВМЪ‡ˆЛ˛ У· ‡Бˆ‡ ‚ ФУОВ, ТУ- Б‰‡‚‡Ъ¸ ТЛЪЫ‡ˆЛ˛, НУ„‰‡ m* > m*c Ë, Ì‡Ó·Ó ÓÚ, ÍÓ„‰‡ m* < m*c . еУМУН ЛТЪ‡ОО˚, ‚˚ ‡˘ВММ˚В ЛБ ТФО‡‚У‚ Bi–Sb, Л ·˚ОЛ ЛТФУО¸БУ‚‡М˚ ‰Оfl ЛБПВ ВМЛИ.
凄МЛЪМ˚В ФУОfl ‰ОЛЪВО¸МУТЪ¸˛ 10 ПНТ ТУБ‰‡- ‚‡ОЛТ¸ ФЫЪВП ‡Б fl‰‡ ·‡Ъ‡ ВЛ НУМ‰ВМТ‡ЪУ У‚ ˜В ВБ ТУОВМУЛ‰ Т П‡О˚П ТУФ УЪЛ‚ОВМЛВП Л Т‡ПУЛМ‰ЫНˆЛВИ, УıО‡К‰ВММ˚И КЛ‰НЛП ‡БУЪУП. ЗУ ‚МЫЪ ВММВП УЪ‚В ТЪЛЛ ТУОВМУЛ‰‡ М‡ıУ‰ЛОТfl ЫБНЛИ НУМВˆ ТУТЫ‰‡ С¸˛‡ ‡, Б‡ФУОМВММУ„У КЛ‰НЛП „ВОЛВП (ЪВПФВ ‡ЪЫ ‡
ЕкДзСн з.Е. оДбйЗхЦ иЦкЦпйСх З еДЙзанзйе ийгЦ |
73 |
НЛФВМЛfl Ф Л МУ П‡О¸МУП ‰‡‚ОВМЛЛ 4,2 д), ‚ НУЪУ-УП ПУМЪЛ У‚‡ОТfl У· ‡БВˆ. уЪУ·˚ У·ВТФВ˜ЛЪ¸ КВТЪНУВ Н ВФОВМЛВ У· ‡Бˆ‡, ТЪ‡Н‡М˜ЛН, ‚ НУЪУ УП М‡- ıУ‰ЛОТfl У· ‡БВˆ, Б‡ФУОМflОТfl Ъ ‡МТЩУ П‡ЪУ М˚П П‡ТОУП, НУЪУ УВ Б‡ПВ Б‡ОУ Ф Л УıО‡К‰ВМЛЛ. уЪУ·˚ У·ВТФВ˜ЛЪ¸ У‰МУ У‰МУТЪ¸ П‡„МЛЪМУ„У ФУОfl ‚МЫЪ Л У· ‡Бˆ‡, П‡„МЛЪМУВ ФУОВ ТУБ‰‡‚‡ОУТ¸ ‚ ‰‚В ТЪЫФВМЛ: ТМ‡˜‡О‡ „ВМВ Л У‚‡ОТfl (Ф Л ФУПУ˘Л ПМУ„У‚ЛЪНУ- ‚У„У ТУОВМУЛ‰‡, М‡ıУ‰fl˘В„УТfl ‚ ‚‡ММВ Т КЛ‰НЛП ‡БУЪУП) ‰ОЛММУФВ ЛУ‰М˚И ЛПФЫО¸Т П‡„МЛЪМУ„У ФУОfl, М‡Ф flКВММУТЪ¸˛ ‚ МВТНУО¸НУ ‰ВТflЪНУ‚ НЛОУ˝ Т- ЪВ‰ ТЪУО¸ МЛБНУИ ˜‡ТЪУЪ˚ ν, ˜ЪУ П‡„МЛЪМУВ ФУОВ ФУОМУТЪ¸˛ Ф УМЛН‡ОУ ‚ У· ‡БВˆ („ОЫ·ЛМ‡ Ф УМЛНМУ‚ВМЛfl δ ‚ МВТНУО¸НУ ‡Б Ф В‚˚¯‡О‡ ‡БПВ ˚ У·-‡Бˆ‡). иУТНУО¸НЫ ‚ П‡„МЛЪМУП ФУОВ Ф У‚У‰ЛПУТЪ¸ ‚ТВ„‰‡ ЫПВМ¸¯‡ВЪТfl, ЪУ ‚ ˝ЪУП МЛБНУ˜‡ТЪУЪМУП ФУОВ БМ‡˜ВМЛВ δ Ы‚ВОЛ˜Л‚‡ОУТ¸ В˘В Л ЛБ-Б‡ ЫПВМ¸¯ВМЛfl σ, Ф Л˜ВП М‡ТЪУО¸НУ, ˜ЪУ Ф Л М‡ОУКВМЛЛ М‡ ‚ЪУ УП ˝Ъ‡ФВ ‚˚ТУНУ˜‡ТЪУЪМУ„У ФУОfl „ОЫ·ЛМ‡ Ф УМЛНМУ‚В- МЛfl δ (10) УТЪ‡‚‡О‡Т¸ ·УО¸¯В ‡БПВ У‚ У· ‡Бˆ‡, ˜ЪУ Л У·ВТФВ˜Л‚‡ОУ У‰МУ У‰МУТЪ¸ П‡„МЛЪМУ„У ФУОfl ‚ В„У У·˙ВПВ.
щЪ‡ ЫТЪ‡МУ‚Н‡ ФУБ‚УОflО‡ ‚ФВ ‚˚В ‚ ПЛ В ФУОЫ˜‡Ъ¸ П‡„МЛЪМ˚В ФУОfl ‰У 60 нО Л Ф У‚У‰ЛЪ¸ ЛБПВ ВМЛfl ˝ОВНЪ УФ У‚У‰МУТЪЛ Л П‡„МЛЪМУИ ‚УТФ ЛЛП˜Л‚УТЪЛ У·-‡БˆУ‚ ‚ Ъ‡НЛı ФУОflı Ф Л ЪВПФВ ‡ЪЫ ‡ı 1,5–4,2 д.
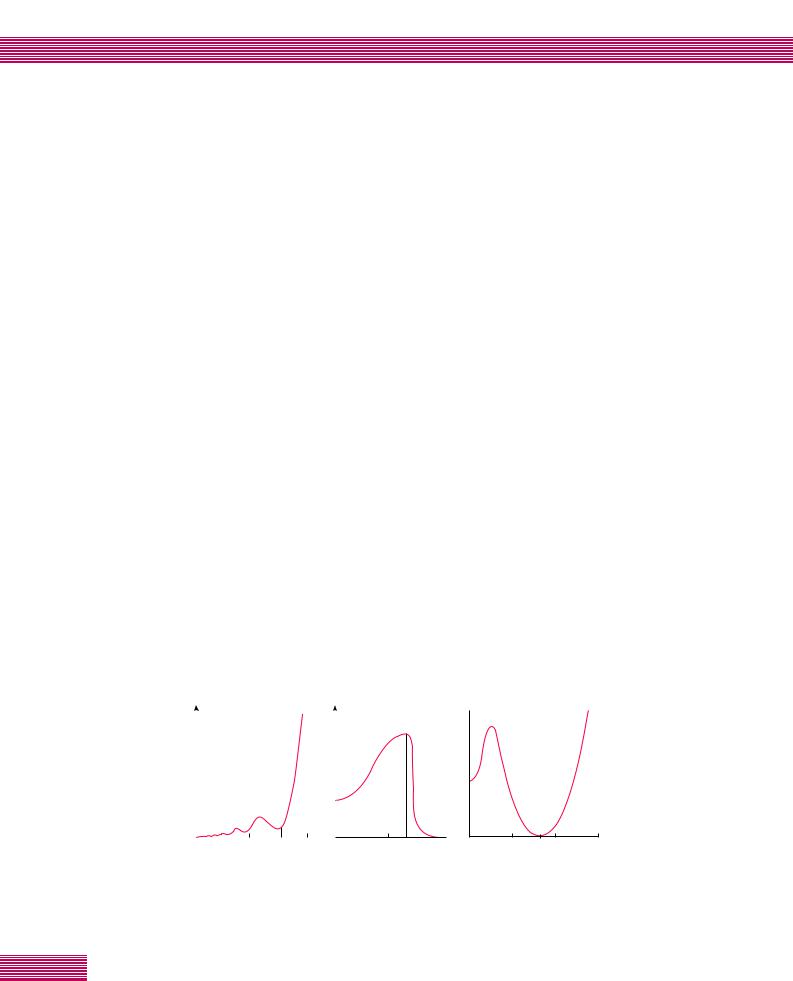
з‡Л·УОВВ М‡„Оfl‰М˚ ВБЫО¸Ъ‡Ъ˚, ФУОЫ˜ВММ˚В Ф Л ЛБПВ ВМЛЛ ˝ОВНЪ Л˜ВТНУ„У ТУФ УЪЛ‚ОВМЛfl У·-‡БˆУ‚. кЛТ. 5, ‡ ЛОО˛ТЪ Л ЫВЪ ı‡ ‡НЪВ ЛБПВМВМЛfl ТУФ УЪЛ‚ОВМЛfl ПУМУН ЛТЪ‡ООЛ˜ВТНУ„У У· ‡Бˆ‡ ТФО‡‚‡ Bi–Sb, НУЪУ ˚И Ф Л Ç = 0 М‡ıУ‰ЛЪТfl ‚ ПВЪ‡О- ОЛ˜ВТНУП ТУТЪУflМЛЛ (‰‚В ТУТВ‰МЛВ БУМ˚ ФВ ВН ˚‚‡- ˛ЪТfl). и Л Ы‚ВОЛ˜ВМЛЛ П‡„МЛЪМУ„У ФУОfl ТУФ УЪЛ‚- ОВМЛВ ТМ‡˜‡О‡, Н‡Н У·˚˜МУ, ПУМУЪУММУ ‚УБ ‡ТЪ‡ВЪ. з‡ ЩУМВ ПУМУЪУММУ„У УТЪ‡ УЪ˜ВЪОЛ‚У ‚Л‰М˚ УТˆЛООflˆЛЛ тЫ·МЛНУ‚‡–‰В Й‡‡Б‡. б‡ЪВП УТˆЛООflˆЛЛ, ı‡ ‡НЪВ М˚В ЛТНО˛˜ЛЪВО¸МУ ‰Оfl ПВЪ‡ООЛ˜ВТНУ„У ТУТЪУflМЛfl Т ЩЛНТЛ У‚‡ММ˚П БМ‡˜ВМЛВП ˝МВ „ЛЛ оВ ПЛ %F , ЛТ˜ВБ‡˛Ъ Л ТУФ УЪЛ‚ОВМЛВ М‡˜ЛМ‡ВЪ ˝НТФУМВМˆЛ‡О¸МУ ·˚ТЪ У Ы‚ВОЛ˜Л‚‡Ъ¸Тfl, ˜ЪУ ЫН‡Б˚‚‡ВЪ
|
‡ |
· |
|
r |
|
r |
|
|
|
|
|
М‡ ФУfl‚ОВМЛВ ˘ВОЛ ‚ ˝МВ „ВЪЛ˜ВТНУП ТФВНЪ В ˝ОВН- Ъ УМУ‚. З ˝ЪУП ТУТЪУflМЛЛ МЛКМflfl БУМ‡ УН‡Б˚‚‡ВЪТfl ФУОМУТЪ¸˛ Б‡ФУОМВМ‡ ˝ОВНЪ УМ‡ПЛ, ‡ ‚В ıМflfl, УЪ- ‰ВОВММ‡fl ˘ВО¸˛ ФЫТЪ‡. З ·УОВВ ТЛО¸М˚ı ФУОflı ТУ- Ф УЪЛ‚ОВМЛВ ТЪ‡МУ‚ЛЪТfl М‡ТЪУО¸НУ ‚ВОЛНУ, ˜ЪУ В„У МВ Ы‰‡ВЪТfl ЛБПВ ЛЪ¸.
й· ‡ЪМ˚И ФВ ВıУ‰ ЛБ ФУОЫФ У‚У‰МЛНУ‚У„У (‰Л- ˝ОВНЪ Л˜ВТНУ„У Ф Л í = 0) ТУТЪУflМЛfl ‚ ПВЪ‡ООЛ˜ВТНУВ, ‚ НУЪУ УП БУМ˚ ФВ ВН ˚‚‡˛ЪТfl, ЛОО˛ТЪ Л Ы- ВЪТfl ЛТ. 5, ·. З ˝ЪУП ТОЫ˜‡В Ф Л Ы‚ВОЛ˜ВМЛЛ ФУОfl ТУФ УЪЛ‚ОВМЛВ ТМ‡˜‡О‡ ‚УБ ‡ТЪ‡ВЪ, ˜ЪУ Т‚flБ‡МУ Т М‡- ОЛ˜ЛВП МВ·УО¸¯У„У НУОЛ˜ВТЪ‚‡ ЪВ ПЛ˜ВТНЛ ‚УБ- ·ЫК‰ВММ˚ı ˝ОВНЪ УМУ‚. б‡ЪВП, Ф Л ФУОflı ‚˚¯В ÇÍ , НУ„‰‡ БУМ˚ М‡˜ЛМ‡˛Ъ ФВ ВН ˚‚‡Ъ¸Тfl, ТУФ УЪЛ‚ОВМЛВ ВБНУ ЫПВМ¸¯‡ВЪТfl Л Ф ЛУ· ВЪ‡ВЪ ПВЪ‡ООЛ˜ВТНЛИ ı‡ ‡НЪВ .
ç‡ ËÒ. 5, ‚ Ф Л‚В‰ВМ‡ Б‡‚ЛТЛПУТЪ¸ ТУФ УЪЛ‚ОВМЛfl УЪ ЛМ‰ЫНˆЛЛ ФУОfl Ç, ı‡ ‡НЪВ М‡fl ‰Оfl ТЛЪЫ‡ˆЛЛ, НУ„‰‡ ‚УБМЛН‡ВЪ ·ВТ˘ВОВ‚УВ ТУТЪУflМЛВ. щЪУЪ В- БЫО¸Ъ‡Ъ М‡Л·УОВВ ЛМЪВ ВТВМ. З ЛТıУ‰МУП ТУТЪУflМЛЛ У· ‡БВˆ fl‚ОflВЪТfl ФУОЫФ У‚У‰МЛНУП (БУМ˚ ‡Б‰ВОВ- М˚ ˘ВО¸˛). ЕО‡„У‰‡ fl М‡ОЛ˜Л˛ ЪВ ПЛ˜ВТНЛ ‚УБ·ЫК- ‰ВММ˚ı МУТЛЪВОВИ ‚ ‚В ıМВИ БУМВ ТУФ УЪЛ‚ОВМЛВ ТМ‡˜‡О‡, Н‡Н У·˚˜МУ, Ы‚ВОЛ˜Л‚‡ВЪТfl. и Л У· ‡БУ‚‡- МЛЛ ·ВТ˘ВОВ‚У„У ТУТЪУflМЛfl ТУФ УЪЛ‚ОВМЛВ ТЛО¸МУ ЫПВМ¸¯‡ВЪТfl. щЪУ Ф УЛТıУ‰ЛЪ ‚ ВБЫО¸Ъ‡ЪВ Ы‚ВОЛ˜В- МЛfl НУМˆВМЪ ‡ˆЛЛ ЪВ ПЛ˜ВТНЛ ‚УБ·ЫК‰ВММ˚ı МУТЛЪВОВИ Ф Л У· ‡˘ВМЛЛ ˝МВ „ВЪЛ˜ВТНУИ ˘ВОЛ ‚ МЫО¸ Л Ы‚ВОЛ˜ВМЛЛ Лı ‰ОЛМ˚ Т‚У·У‰МУ„У Ф У·В„‡ [4] ‚ ˝ОВНЪ Л˜ВТНУП ФУОВ; ‚˚¯В ЫН‡Б˚‚‡ОУТ¸, ˜ЪУ ˝ЪУ УТУ·УВ ТУТЪУflМЛВ Т УТУ·˚П Б‡НУМУП ‰ЛТФВ ТЛЛ. б‡- ЪВП БУМ˚ М‡˜ЛМ‡˛Ъ ‡ТıУ‰ЛЪ¸Тfl, НУМˆВМЪ ‡ˆЛfl МУТЛЪВОВИ ЫПВМ¸¯‡ВЪТfl Л ТУФ УЪЛ‚ОВМЛВ ‚МУ‚¸ М‡˜Л- М‡ВЪ ‡ТЪЛ.
бДдгыуЦзаЦ
к‡ТТПУЪ ВММ˚В Щ‡БУ‚˚В ФВ ВıУ‰˚ ‚В˘ВТЪ‚ ‚ П‡„МЛЪМУП ФУОВ ЫН‡Б˚‚‡˛Ъ М‡ УЪМУТЛЪВО¸М˚И ı‡ ‡НЪВ ‡Б‰ВОВМЛfl ‚В˘ВТЪ‚ М‡ ПВЪ‡ОО˚, ФУОЫФ У-
‚
r 
0 |
30 BÍ 60 |
0 |
30 BÍ |
0 |
20 BÍ 40 |
60 |
|
|
|
B, íÎ |
|
|
|
êËÒ. 5. ᇂЛТЛПУТЪЛ ˝ОВНЪ Л˜ВТНУ„У ТУФ УЪЛ‚ОВМЛfl r У· ‡БˆУ‚ Ф Л Щ‡БУ‚˚ı ФВ ВıУ‰‡ı ‚ П‡„МЛЪМУП ФУОВ Ç: ‡ – ЛБ ПВЪ‡ООЛ˜ВТНУ„У ‚ ‰Л˝ОВНЪ Л˜ВТНУВ ТУТЪУflМЛВ; · – ЛБ ФУОЫФ У‚У‰МЛНУ‚У„У (‰Л˝ОВНЪ Л˜ВТНУ„У Ф Л í = 0 д) ‚ ПВ- Ъ‡ООЛ˜ВТНУВ; ‚ – ФУТОВ‰У‚‡ЪВО¸МУ ЛБ ФУОЫФ У‚У‰МЛНУ‚У„У Ф Л Ç = 0 ‚ ·ВТ˘ВОВ‚УВ Л ЛБ ·ВТ˘ВОВ‚У„У ТМУ‚‡ ‚ ФУОЫФ У‚У‰МЛНУ‚УВ ТУТЪУflМЛВ. ÇÍ – ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ Н ЛЪЛ˜ВТНЛВ БМ‡˜ВМЛfl ЛМ‰ЫНˆЛЛ ‰Оfl ˝ЪЛı ФВ ВıУ‰У‚
74 |
лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹1, 1999 |

‚У‰МЛНЛ Л ‰Л˝ОВНЪ ЛНЛ. ЗУ ‚ТflНУП ТОЫ˜‡В ТОВ‰ЫВЪ ЛПВЪ¸ ‚ ‚Л‰Ы, ˜ЪУ Ъ‡Н‡fl НО‡ТТЛЩЛН‡ˆЛfl ТФ ‡‚В‰ОЛ‚‡ ОЛ¯¸ Ф Л УЪТЫЪТЪ‚ЛЛ ‚МВ¯МЛı, М‡Ф ЛПВ П‡„МЛЪМУ„У, ФУОВИ. З П‡„МЛЪМУП ФУОВ У‰МУ Л ЪУ КВ ‚В˘ВТЪ- ‚У ‚ Ф ЛМˆЛФВ ПУКВЪ ·˚Ъ¸ Л ‰Л˝ОВНЪ ЛНУП, Л ФУОЫ- Ф У‚У‰МЛНУП, Л ПВЪ‡ООУП.
аБ‚ВТЪМУ, ˜ЪУ ‚У ЗТВОВММУИ, ‚ ˜‡ТЪМУТЪЛ ‚ ‡ИУ- М‡ı МВИЪ УММ˚ı Б‚ВБ‰, ПУ„ЫЪ ТЫ˘ВТЪ‚У‚‡Ъ¸ МВУ- ·˚˜‡ИМУ ТЛО¸М˚В П‡„МЛЪМ˚В ФУОfl, ‰УТЪЛ„‡˛˘ЛВ Щ‡МЪ‡ТЪЛ˜ВТНУИ ‚ВОЛ˜ЛМ˚ 108–109 нО. ЗВ˘ВТЪ‚У, ФУФ‡‰‡˛˘ВВ ‚ Ъ‡НЛВ ФУОfl, ПУКВЪ Н‡˜ВТЪ‚ВММУ ЛБПВМЛЪ¸ Т‚УЛ Т‚УИТЪ‚‡: ‰Л˝ОВНЪ ЛН ПУКВЪ Ф ЛУ· ВТЪЛ ПВЪ‡ООЛ˜ВТНЫ˛ Ф У‚У‰ЛПУТЪ¸ Л, М‡У·У УЪ, ПВЪ‡ОО ТЪ‡Ъ¸ ‰Л˝ОВНЪ ЛНУП.
З О‡·У ‡ЪУ Лflı ПЛ ‡ ‚В‰ЫЪТfl ‡·УЪ˚ ФУ ТУБ‰‡- МЛ˛ МУ‚˚ı ПВЪУ‰У‚ ФУОЫ˜ВМЛfl ТЛО¸М˚ı Л Т‚В ı- ТЛО¸М˚ı П‡„МЛЪМ˚ı ФУОВИ [6]. З М‡ТЪУfl˘ВВ ‚ ВПfl Ы‰‡ВЪТfl ФУОЫ˜‡Ъ¸ ФУОfl Т ЛМ‰ЫНˆЛВИ ‚ МВТНУО¸НУ Ъ˚- Тfl˜ ЪВТО‡. щЪУ УЪН ˚‚‡ВЪ МУ‚˚В ‚УБПУКМУТЪЛ ‰Оfl ЛТТОВ‰У‚‡МЛfl ‡БОЛ˜МУ„У ЪЛФ‡ Щ‡БУ‚˚ı ФВ ВıУ‰У‚ ‚В˘ВТЪ‚‡ ‚ П‡„МЛЪМУП ФУОВ Л ТЫ˘ВТЪ‚ВММУ ‡Т¯Л-flВЪ ˜ЛТОУ ‚УБПУКМ˚ı У·˙ВНЪУ‚ ‰Оfl Ф У‚В‰ВМЛfl ЛБПВ ВМЛИ. З ˜‡ТЪМУТЪЛ, ЫКВ ТВИ˜‡Т ‚УБПУКМУ У·М‡ Ы- КЛЪ¸ ФВ ВıУ‰ ЛБ ПВЪ‡ООЛ˜ВТНУ„У ‚ ‰Л˝ОВНЪ Л˜ВТНУВ ТУТЪУflМЛВ Ы Bi, Sb Л, ФУ-‚Л‰ЛПУПЫ, „ ‡ЩЛЪ‡.
з‡НУМВˆ, ‡ТТПУЪ ВММ˚В ФВ ВıУ‰˚ ПУКМУ ЛТФУО¸БУ‚‡Ъ¸ Н‡Н ВФВ М˚В ЪУ˜НЛ Ф Л „ ‡‰ЫЛ У‚НВ ¯Н‡О˚ Т‚В ıТЛО¸М˚ı П‡„МЛЪМ˚ı ФУОВИ.
ь‚ОВМЛВ Щ‡БУ‚˚ı ˝ОВНЪ УММ˚ı ФВ ВıУ‰У‚ ·˚ОУ УЪН ˚ЪУ ‡‚ЪУ УП ТЪ‡Ъ¸Л ТУ‚ПВТЪМУ Т Ц.А. л‚ЛТЪУ- ‚УИ, л.е. уЫ‰ЛМУ‚˚П Л А.А. А· ЛНУТУ‚˚П Л ‚МВТВ-
ÌÓ ‚ ÉÓÒÛ‰‡ ÒÚ‚ÂÌÌ˚È ÂÂÒÚ ÓÚÍ ˚ÚËÈ ëëëê ÔÓ‰ ÌÓÏ ÓÏ 156.
ганЦкДнмкД
1.АÁ·Âθ å.ü., Å ‡Ì‰Ú ç.Å. // èËҸχ ‚ Üùíî. 1965. í. 48. ë. 1206–1209.
2.Å ‡Ì‰Ú ç.Å., ë‚ËÒÚÓ‚‡ Ö.А. // ìÒÔÂıË ÙËÁ. ̇ÛÍ. 1970. í. 101, ‹ 2. ë. 249–272.
3.åflÍ˯‚ É.ü., ÅÛıÓ‚ˆÂ‚ Å.Å. оЛБЛН‡ 10. е.: и УТ‚В- ˘ВМЛВ, 1987. ЙО. п.
4.Å ‡Ì‰Ú ç.Å. зУ‚˚И НО‡ТТ ЩУЪУФ У‚У‰fl˘Лı ‡‰Л‡- ˆЛУММУТЪУИНЛı ФУОЫФ У‚У‰МЛНУ‚˚ı П‡ЪВ Л‡ОУ‚ // лУ УТУ‚ТНЛИ й· ‡БУ‚‡ЪВО¸М˚И ЬЫ М‡О. 1997. ‹ 4. л. 65–72.
5.ÅÛıÓ‚ˆÂ‚ Å.Å., дОЛПУМЪУ‚Л˜ ы.г., åflÍ˯‚ É.ü. оЛБЛН‡ 9. е.: и УТ‚В˘ВМЛВ, 1988. ЙО. XI.
6.ɇȉÛÍÓ‚ û.è. оЛБЛ˜ВТНЛВ УТМУ‚˚ Л ПВЪУ‰˚ ФУОЫ- ˜ВМЛfl П‡„МЛЪМУ„У ФУОfl // лУ УТУ‚ТНЛИ й· ‡БУ‚‡- ЪВО¸М˚И ЬЫ М‡О. 1996. ‹ 4. л. 97–105.
* * *
зЛНУО‡И ЕУ ЛТУ‚Л˜ Е ‡М‰Ъ, ‰УНЪУ ЩЛБЛНУ-П‡- ЪВП‡ЪЛ˜ВТНЛı М‡ЫН, Ф УЩВТТУ , Б‡‚. УЪ‰ВОВМЛВП ЩЛБЛНЛ Ъ‚В ‰У„У ЪВО‡ ЩЛБЛ˜ВТНУ„У Щ‡НЫО¸ЪВЪ‡ еЙм, Б‡ТОЫКВММ˚И ‰ВflЪВО¸ М‡ЫНЛ клолк, Б‡ТОЫКВММ˚И Ф УЩВТТУ еЙм, О‡Ы В‡Ъ ЙУТЫ‰‡ ТЪ‚ВММ˚ı Ф ВПЛИ лллк Л кУТТЛЛ, Ф ВПЛЛ ЛП. з.С. и‡Ф‡ОВНТЛ Л бУОУЪУИ ПВ‰‡ОЛ ЛП. и.з. г·‰‚‡ Аз лллк,
гУПУМУТУ‚ТНЛı Ф ВПЛИ еЙм. й·О‡ТЪ¸ М‡Ы˜М˚ı ЛМЪВ ВТУ‚ – ЩЛБЛН‡ МЛБНЛı ЪВПФВ ‡ЪЫ . А‚ЪУ ‰‚Ыı УЪН ˚ЪЛИ, 30 Ф‡ЪВМЪУ‚ Л ЛБУ· ВЪВМЛИ, ТВПЛ Ы˜В·- МЛНУ‚ Л ПУМУ„ ‡ЩЛИ, 27 ПУМУ„ ‡ЩЛ˜ВТНЛı У·БУ У‚ Л ·УОВВ 500 М‡Ы˜М˚ı ‡·УЪ.
ЕкДзСн з.Е. оДбйЗхЦ иЦкЦпйСх З еДЙзанзйе ийгЦ |
75 |

76 |
лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹1, 1999 |
