На материальную точку действуют и

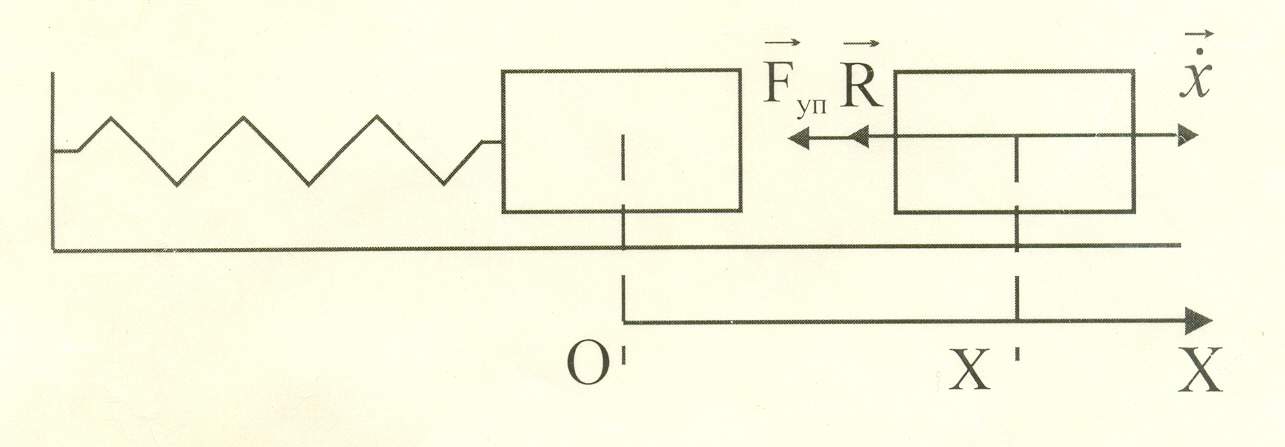
Дифференциальное уравнение движения:

, если заменить , то (Б)

Движение материальной точки при наличии вязкого сопротивления описывается дифференциальным уравнением второго порядка линейным однородным с постоянными коэффициентами. Поэтому свободные колебания и свободные колебания при вязком сопротивлении называются линейными колебаниями.

Характеристическое уравнение дифференциального уравнения (Б) будет:

, его корни

Возможны случаи:

I Случай (относительно малое сопротивление). Корни:

, где

Общее решение уравнения (Б)

(Б^/)

Сменив постоянные интегрирования на а и

, получим

(Б^//)

График движения будет:

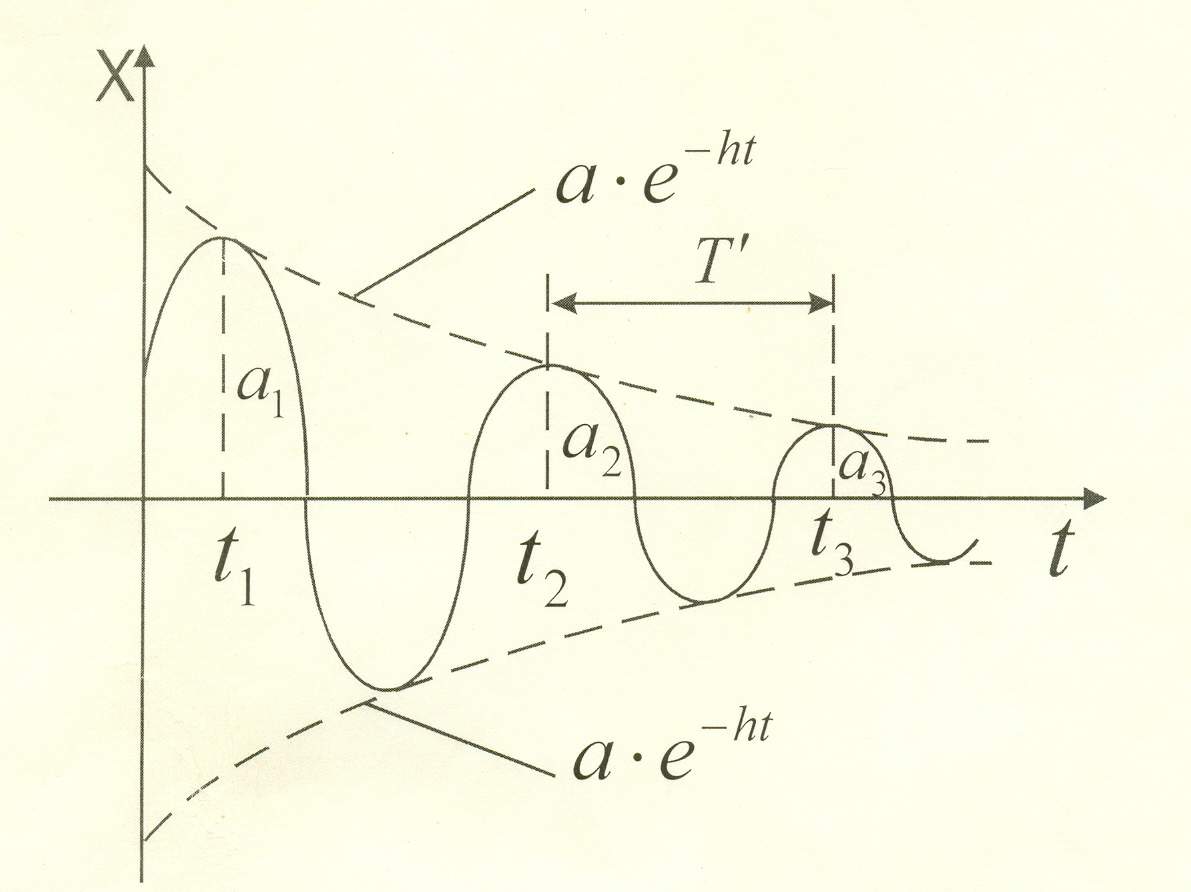
Проанализируем уравнение (Б^//).

1. При действии на материальную точку восстановительной силы 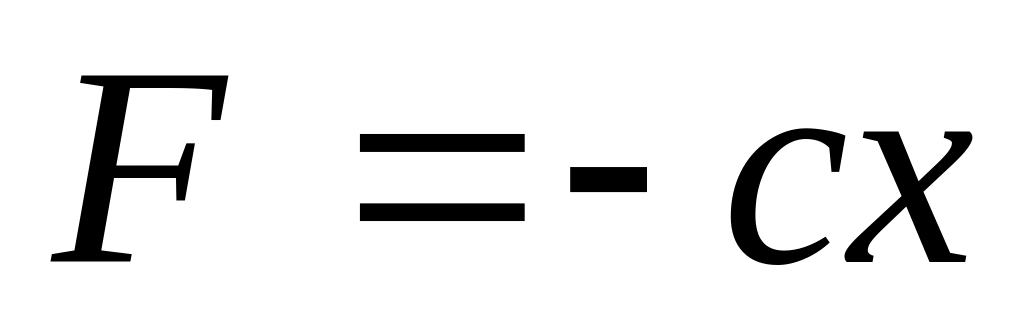и силы сопротивления 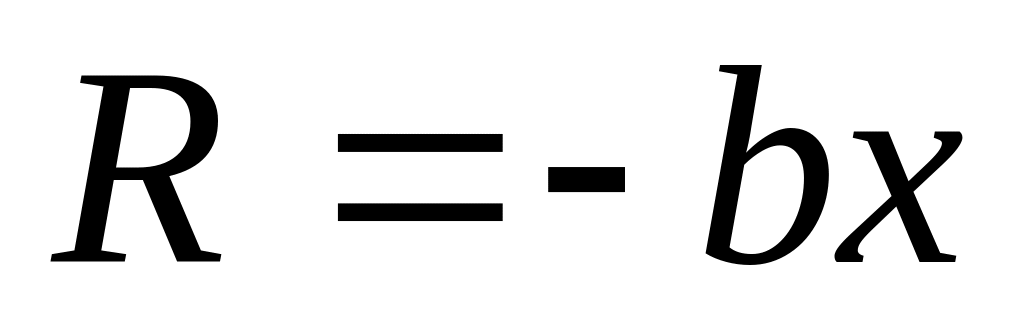малой по сравнению с F(k h) точка совершает колебания.

2. Причем максимальные отклонения (размахи) точки от положения равновесия со временем уменьшается, но повторяется через одинаковые промежутки времени Т^/.

Такие колебания называются свободными затухающими при вязком сопротивлении.

3. Составив выражения Т^/ и Т можно заключить, что при одинаковых параметрах с и m период затухающих колебаний больше периода колебаний без вязкого сопротивления (Т^/> Т).

Характеристикой быстроты затухания является декремент колебаний:

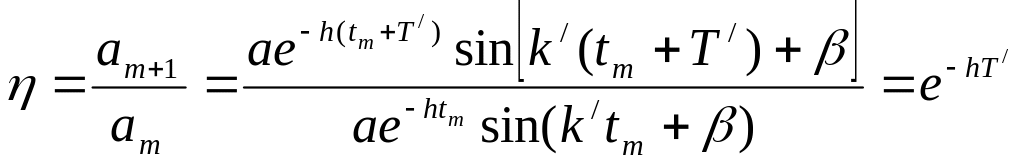
или логарифмический декремент –hT^/.

II Случай (редкий)

, тогда решение уравнения (Б)

, подставив начальные условия

Частное решение:

Возможны разные графики движения при различных начальных условиях

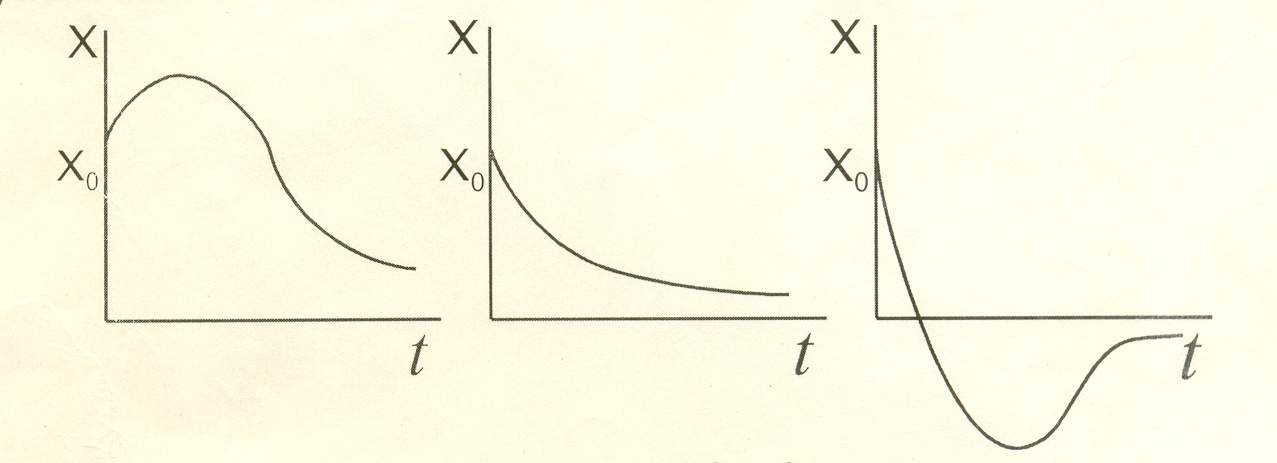
III Случай

– оба корня вещественные и отрицательные.

Общее решение уравнения (Б)

Графики движения аналогичны случаю 2. При действии на материальную точку восстанавливающей силы и достаточно большой силы вязкого сопротивления движение будет апериодическим и носит ­затухающий характер.

Вынужденные колебания.

На материальную точку действует восстанавливающая сила и возмущающая сила .

Рассмотрим частный случаи гармонической возмущающей силы, часто встречающийся в практике.

Дифференциальное уравнение движения:

, или обозначив ;

(В)

Решение уравнения (В): , где

– общее решение соответствующего однородного уравнения.

– частное решение уравнения (В), которое будем искать в форме правой части.

Постоянную А найдем из условия удовлетворения уравнения (В):

или

Из условия соблюдения полученного равенства при любом t

Т.о. полное решение уравнения (В) будет:

При наличии гармонической возмущающей силы движение материальной точки складывается из двух колебаний:

• колебаний с частотой "k" свободных колебаний, называемых собственным

• колебаний с частотой возмущающей силы, называемых вынужденными

Амплитуда "а" собственных колебаний определяется начальными условиями, но она не равна амплитуде свободных колебаний, т.к. она зависит так же от параметров возмущающей силы.

В частности, при нулевых начальных условиях собственные колебания существуют при .

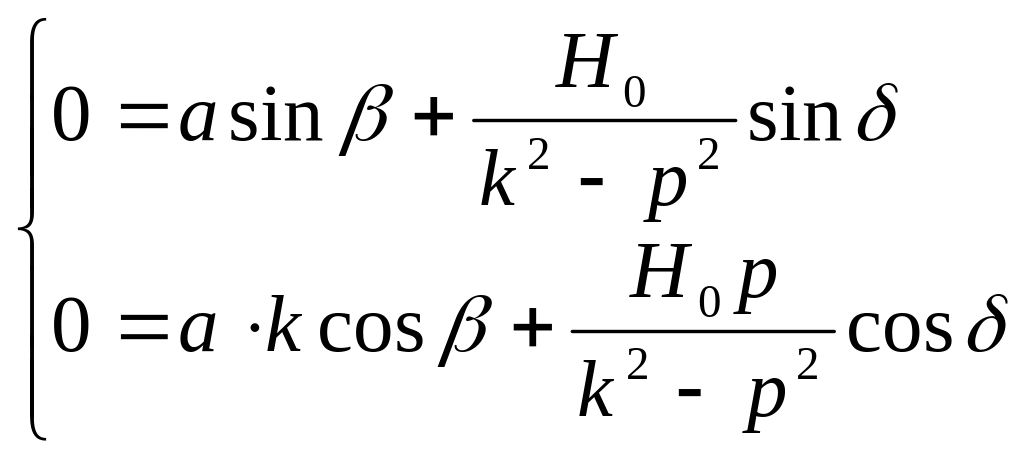, откуда

Амплитуда А вынужденных колебаний зависит от соотношения частот k и р. Преобразуем выражение для А

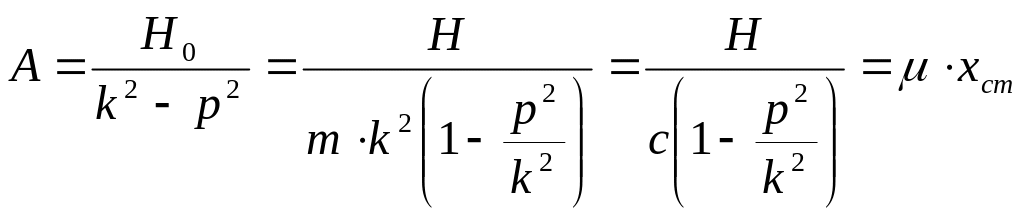
здесь – статическое отклонение материальной точки при приложении максимально возможной силы.

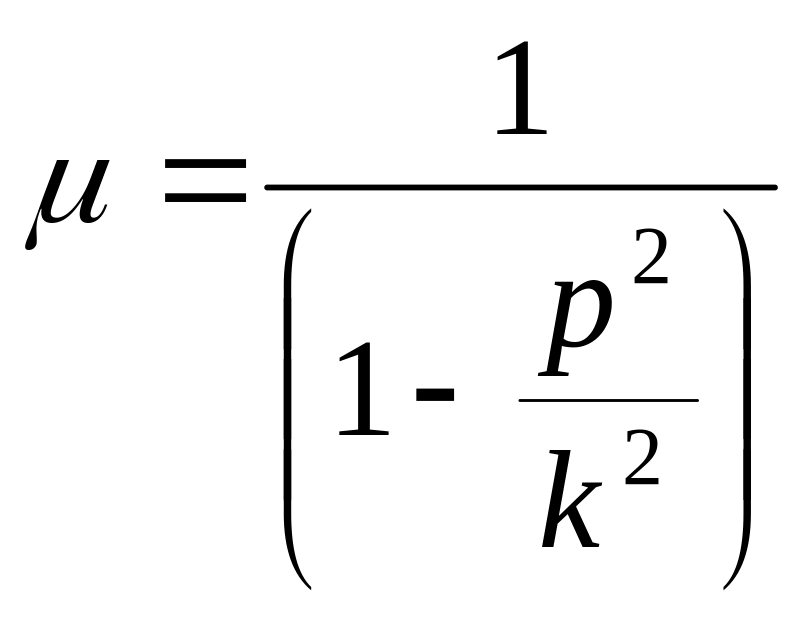– коэффициент динамичности, характеризует амплитуду вынужденных колебаний при данных параметрах системы (с) и возмущающей силы (Н).

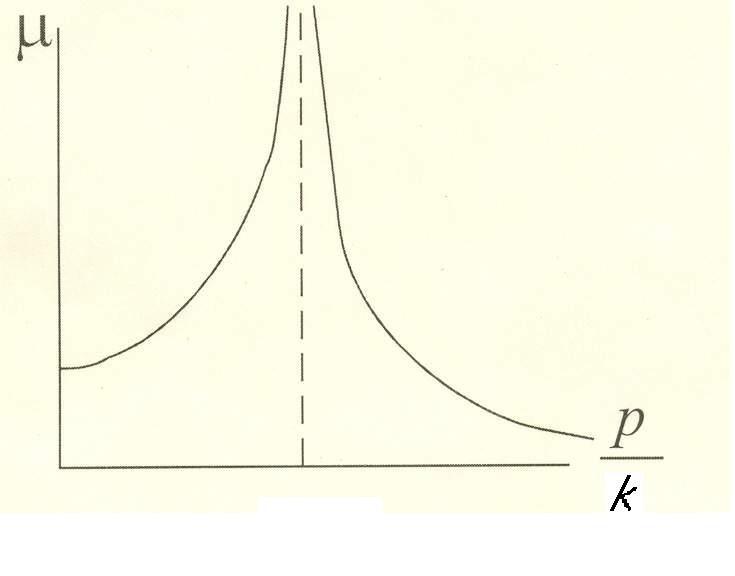
При малых, по сравнению с k частотах вынужденных колебаний р

При больших частотах ( ) А – малы. При – явление резонанса.

Вынужденные колебания при вязком сопротивлении.

На материальную точку действуют силы и .

Дифференциальное уравнение движения:

(Г)

Полное решение уравнения (Г) будет , где

– общее решение соответствующего однородного уравнения (Б)

– частное решение в форме правой части.

Постоянные А и из условий удовлетворяющих уравнениям:

полное решение:

(Г^/)

При наличии вязкого сопротивления движение материальной точки под действием F и Q складывается из колебаний с частотой k^/ собственных затухающих колебаний и колебаний вынужденных с частотой р возмущающей силы Q. Первое слагаемое из-за затухающего характера интереса не представляет.