§ 5. Смешанная краевая задача для уравнения параболического типа. Нестационарный теплообмен при перевозке нефти трубопроводом.

5.1. Постановка задачи

П одогретый до температуры θ₁ (град.) нефть перевозится по подземному трубопроводу.

Глубина прокладки нефтепровода Н(м).

Считая, ч то теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.

х Н О

Рис. 14

5.2. Математическая модель.

Ось ОХ направим вертикально вверх (рис. 14). На оси ОХ выделим элемент с координатами х и х + Δх. Тогда приращение энергии в направлений оси х за время Δt будет

(7.1)

С другой стороны, согласно закону сохранения энергий,

(7.2)

Левые части (7.1) и (7.2) равны, поэтому

где ρ– плотность грунта [кг/м³];

с – массовая теплоемкость грунта [кдж/кг.град];

λ – коэффициент теплопроводности грунта [вт/м·град.].

При х = 0 задается температура 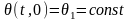. На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).

В основу изучения конвективного теплообмена положен закон Ньютона-Рихмана

где q – плотность теплового потока, вт/м²;

θ₀ – температура воздуха, ⁰С;

θ_гр – температура поверхности грунта,⁰С;

α – коэффициент теплоотдачи, вт/(м²·град);

Согласно закону сохранения энергии, количество теплоты, отдаваемый единицей поверхности тела окружающей среде за единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.

(7.3)

Равенство (7.3) является математической формулировкой граничного условия третьего рода; оно является действительной для каждого момента времени t.

называется граничным условием первого рода.

Получена задача: найти решение нестационарного параболического уравнения со смешанными граничными условиями, т.е.

(7.4)

θ(t,0) = θ₁ = const (7.5)

(7.6)

(7.7)

Теорема 1. При определенных условиях на ρ(θ), с(θ) и λ(θ) задача (7.4) - (7.7) имеет единственное решение.

7.3. Приближенный метод решения задачи (7.4) – (7.6).

Решение задачи (7.4) – (7.6) зависит от двух переменных , где t – время, час; х – координата точки грунта, м. Поэтому задача (7.4) – (7.6) решается в области

Q= (0, Т_max)·(0,H),

Сетка. Отрезок [0, H] разбиваем на N равных частей с шагом h = H/N, а отрезок [0, T_max] на М равных частей с шагом ∆t = T_max /M. Тогда получается сетка (рис. 2).

В рис.2 «крестиками» - х обозначены граничные узлы, а «ноликами» - 0 обозначены внутренние узлы.

Н х х х х х х о о о о х о о о о х х х х х t Тmax Рис. 2

А ппроксимация выражений

т.е. функций ρ(θ) и с(θ) определяются на нижних слоях. В начальный момент времени, т.е. при

.

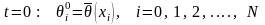Вместо задачи (7.4) – (7.7) решается приближенная задача

(7.8)

(7.9)

(7.10)

В системе (7.8) i = 1, 2, …, N-1 при каждом j=0,1,…,M-1.