20. Циклические коды. Порождающий многочлен циклического кода, проверочный многочлен;

Синдром циклического кода, теорема о синдроме циклического кода.

Пусть C – код в пространстве , тогда C называется циклическим если

Пример (могут просить написать):

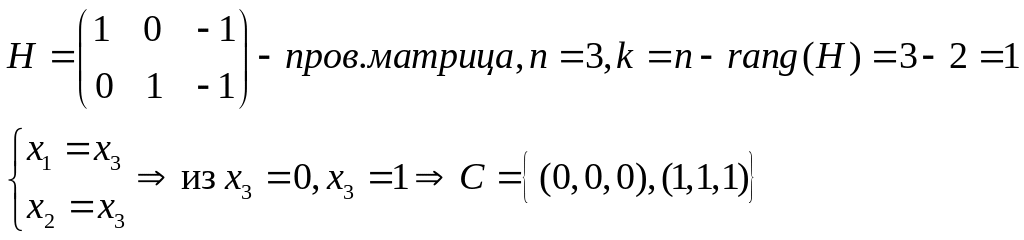
Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ — коды), коды Рида-Соломона. Введем преобразование, называемое циклическим сдвигом . Данное преобразование - линейное преобразование.Циклические коды в - это в точности все инвариантные подпространства относительно циклического сдвига.

Запись элементов из в виде многочленов (описание циклических кодов как идеалов в кольце многочленов): Можно записать элементы поля в виде многочленов и тогда рассматривать циклические коды как иделы в кольце многочленов. - сопоставление.

Для многочленов, степень которых меньше или равна n-1, соответствие взаимно однозначное.

Рассмотрим множество многочленов вида , - поржденный им идеал в кольце многочленов . Рассмотрим факторкольцо: . Оно состоит из различных правых (левых) смежных классов по идеалу . Для удобства каждый такой класс можно заменить на его представителя, а в качестве различных представителей взять многочлены из степень которых не превышает . Т.о., фактор-кольцо можно считать состоящим из многочленов степени, не большей, чем с коэффициентами из . Сложение и умножение в этом кольце осуществляется по модулю многочлена . М/у элементами данного факторкольца и элементами пространства существует взаимнооднозначное соответствие, причем при данном соответствии сохраняются операции сложения и умножения на скаляр.

Опр. Подкольцо – подмножество кольца, которое само являющееся кольцом относительно главных бинарных операций кольца.

Опр. Идеал. Правый (левый) идеал – такое подкольцо кольца, умножение всех элементов которого справа(слева) на элемент кольца принадлежит идеалу. Если верны оба утверждения, множество называется двусторонним идеалом. Если операция коммутативна, используется понятие идеал.

Теорема «О представлении циклического кода в виде идеала»: Пусть С – линейный код в . С является цикличным кодом тогда и только тогда ( ), когда соответствующее ему множество многочленов в кольце является идеалом.

Доказательство: Предположим, что С- циклический код: , соответствующий ему многочлен имеет вид: , Необходимо показать что является идеалом кольца . Проверим. Очевидно, что - подкольцо, т.к. - замкнуто по сложению, поскольку , то и . Для того, чтобы показать что произведение элементов из вновь находится в , докажем утверждение:

Доказательство утверждения: a) . Т.к в кольце К где результат циклического сдвига. Т.к. С- цикличен, то и , то

б) .

из свойства «а» для идеалов следует, что , но тогда из свойства «б» следует, что . При умножении одного многочлена на другой получим сумму указанных произведений, каждое из которых принадлежит I. Но так как I замкнуто по сложению, получим что произведение 2-х многочленов, один из которых принадлежит кольцу К, а второй подкольцу I лежит в I. . Из данного включения следует, что является подкольцом и идеалом кольца К. что и требовалось показать.

1) Рассмотрим множество и пусть - идеал. Необходимо показать, что код С – цикличен. Возьмем произвольное . Необходимо показать, что . По условию: . Т.к. - идеал, то . Другими словами: , т.е. .Что и требовалось доказать.

Порождающий и проверочный многочлен циклического кода.

Предположим, что код С имеет ненулевую размерность. Среди многочленов, входящих в С, отличных от нуля, найдем многочлен с наименьшей степенью (таких многочленов может быть и несколько).

Утверждение «О многочлене »:

Доказательство: поделим многочлен на многочлен с остатком. Получим:

. Т.к. С – идеал, то . Но ; . В противном случае получаем противоречие с корректностью выбора .

Замечание: Заметим, что , который был описан выше, обладает свойством: или (что одно и то же) , т.е. С порождается . Это следует из того, что С – идеал и последнего утверждения, в котором мы получаем, что все многочлены из С представимы через .

Опр.: Многочлен циклического кода С, описанный выше, называется порождающим многочленом данного кода.

Замечание: Заметим, что два различных порождающих многочлена одного и того же кода получаются друг из друга путем умножения на константу. Поэтому в качестве берут тот, у которого старший коэффициент равен 1.

Теорема «О порождающем многочлене»: Пусть - порождающий многочлен циклического кода С в , тогда многочлен делит многочлен .

Доказательство: Поделим многочлен на с остатком. Получим: . В кольце К: . Поскольку .

Эта теорема позволяет перечислять все циклические коды определенной длинны, указывая их порождающие многочлены.

Опр.: Пусть С – циклический код с порождающим многочленом и длиной кодового слова равной , тогда проверочным многочленом кода С называется многочлен вида: .

Замечание: Т.к. все порождающие многочлены одного кода отличаются друг от друга на константу, то и все проверочные многочлены отличаются на константу. Обычно, в качестве проверочного многочлена выбирают тот, у которого коэффициент при старшем члене равен 1.

Требование к порождающему полиному при кодировании – его вес не должен быть меньше минимального кодового расстояния

В теории информации циклические коды часто записываются как и k соответствует числу информационных символов, а m- проверочных

С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:

• несистематическое кодирование осуществляется путём умножения кодируемого вектора на g(x): c(x) = u(x)g(x) – векторы сначала переписываются в виде соответствующих полиномов, а затем перемножаются, после чего записывается вектор, соответствующий ответу

• систематическое кодирование осуществляется путём «дописывания» к кодируемому слову остатка от деления 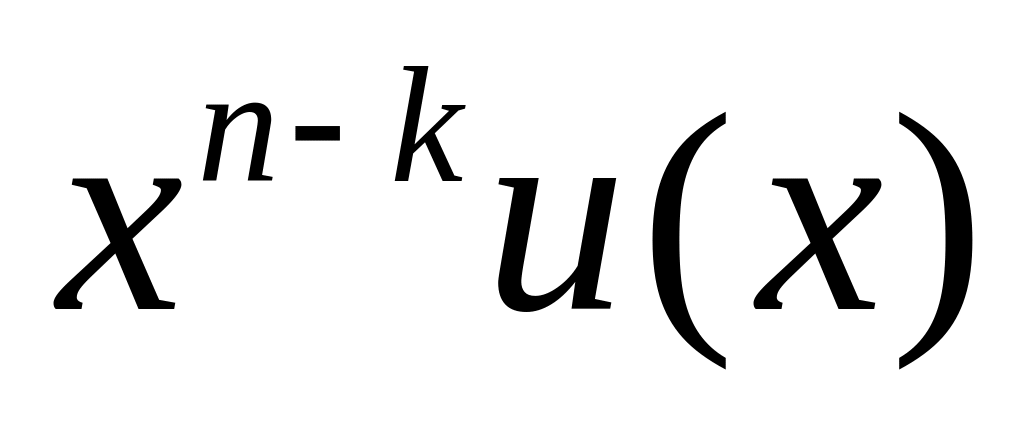на g(x), deg(g(x)) = n-k, 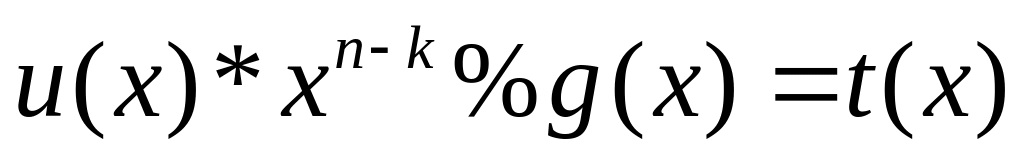то есть .

deg(u(x))=k-1; x^n-i - t_i(x)=ci(x)- линейно независимые кодовые многочлены, получаем t_i(x) имеющий макс степень n-k-1; , по ним строим порождающую матрицу:

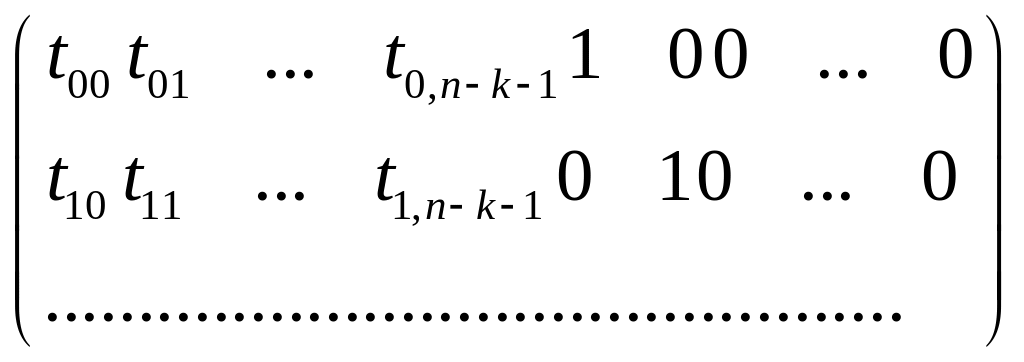, проверочная матрица строится исходя из формулы G=[T:E] ->H=[E:T^t]

Обнаружение ошибок кодирования (при передаче в канале с помехами)

Будем рассматривать несистематическое кодирование. Пусть мы получили сообщение

Очевидно, что если сообщение будет передано без ошибок , то для полученного кодового слова будет выполняться , если же в ходе передачи возникли ошибки, то остаток будет отличен от нуля. При этом заметим, что так как вычисления идут по модулю многочлена - это и есть смысл выбора проверочного многочлена

Теорема:

Если а(х)∈С, то а(х)*h(x)=0;

Если а(х) С, то а(х)*h(x)≠0;

Доказательство:

1) а(х)∈С --> a(x)=b(x)*g(x);

a(x)*h(x)=b(x)*g(x)*h(x)=b(x)(xⁿ+1)=0 mod(xⁿ+1);

2) а(х) С --> a(x)=b(x)*g(x)+r(x);

a(x)*h(x)=b(x)(xn+1)+r(x)h(x)

deg(a(x))=n-k; deg(h(x))=k; deg(r(x)h(x))<=n-1;

а(х)*h(x)=r(x)*h(x)≠0

Доказано.

Синдром – это вектор (в указанном определении –вектор-строка) - определяемый через проверочную матрицу. Можно записать соответствующий ему многочлен .

Учитывая, что получим, сто синдром равен

И соответственно по синдрому можно определить вектор ошибок. (На практике такой поиск обычно осуществляют по заранее составленным таблицам).

Свойства синдрома:

1) .

2) .

3) .

4) (равенство смежных классов).

Доказательство:

1. Следует из определения проверочной матрицы.

2. .

3. .

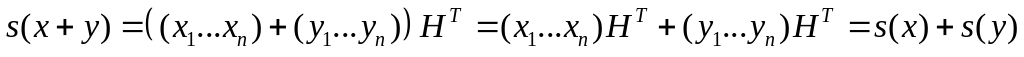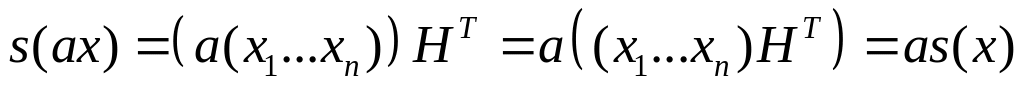4. Используем критерий равенства правых смежных классов в абелевой группе ( - группа, (С, +) - подгруппа):

.

Опр.: Пусть - подмножество, ( - непустое множество), тогда х≠0 – лидер М, если он имеет минимальный вес Хэменга, т.е. .

Утверждение «О ближайшем соседе»: Пусть С – код в , его проверочная матрица. , тогда будет ближайшим элементом к элементу , в смысле расстояния Хэменга, элемент будет лидером смежного класса с синдромом .

Доказательство: Заметим, что действительно содержится в классе, определяемом :

. Пусть х – ближайший сосед, т.е Если элемент пробегает все кодовые слова, то элемент пробегает все элементы смежного класса , т.е. . Другими словами, лидер смежного класса .

Пусть - лидер смежного класса . Т.е. . Другими словами: . Следовательно, х – ближайший сосед. Утверждение доказано.

Алгоритм декодирования с помощью синдромов и лидеров:

1. Найти проверочную матрицу для кода С.

2. Перечислить все смежный классы по и для каждого класса указать соответствующий ему синдром и выбрать какого-либо лидера этого класса.

3. Для полученного сообщения вычисляется его синдром .

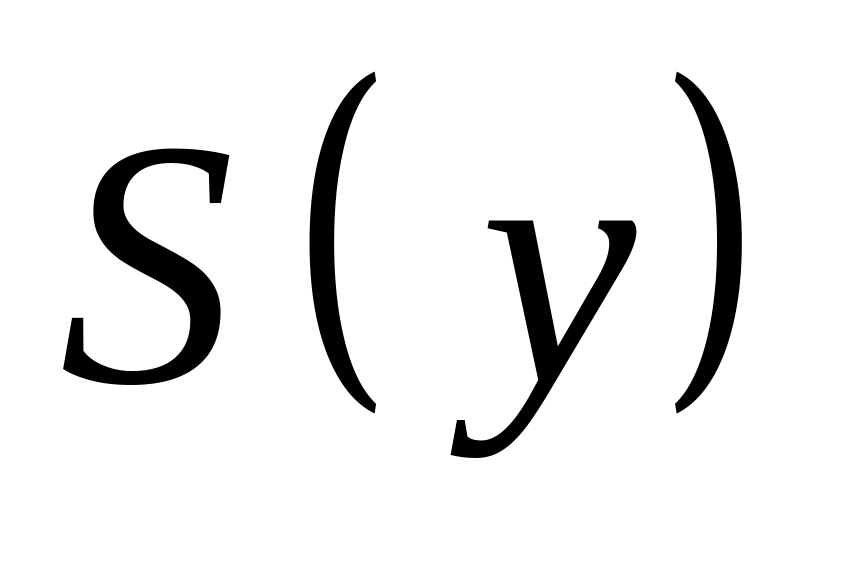4. По полученному синдрому найти соответствующий ему лидер

5. Декодировать , где

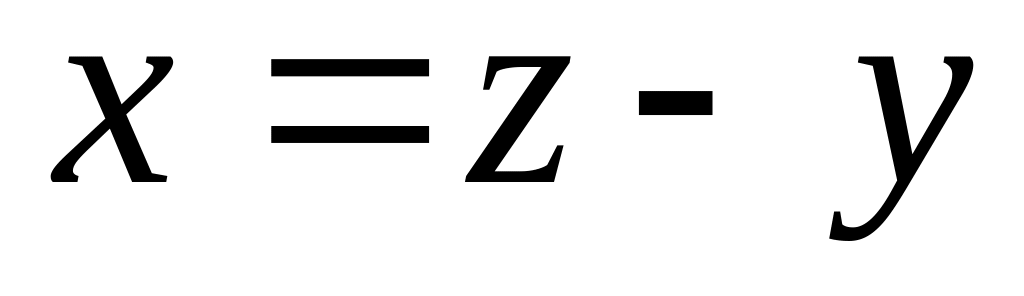
Можно написать алгоритм и для случая использования многочленов

В этом случае процедура декодирования имеет следующий вид:

1. Найдем синдромный многочлен

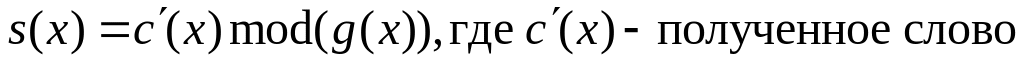
2. Для каждого вычислим до тех пор, пока не будет найден такой, что максимальное число ошибок, исправляемых кодом.

3. Полином ошибки есть

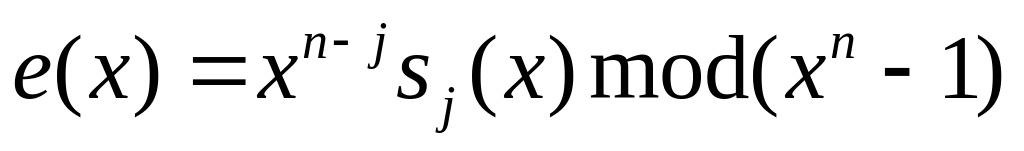
Так, для кодов Хэмминга получаемый синдром просто совпадает с вектором ошибок

Циклический код не обнаружит ошибок в полученной комбинации только в том случае, если количество ошибок таково, что перевело одну разрешенную кодовую комбинацию в другую( то есть полученное нами слово так же принадлежит коду), и не сможет исправить ошибки в том случае, если их количество превысит число проверочных символов.

Однако, обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации

(на всякий случай - было в лекциях по кодированию)

Теорема о синдроме циклического кода:

Пусть d* - минимальное кодовое растояние циклического кода. Каждому многочлену ошибок веса < соответствует единственный синдромный многочлен.

Доказательство:

Даны многочлены соотв векторам ошибок e1(x), e2(x), w(e1)< , w(e2)< , e1(x) = c1(x)+S(x), e2(x)=c2(x)+S(x), e1(x)-e2(x)=c1(x)-c2(x)

e1(x)=e2(x)+c(x); w(e1(x)-e2(x))<d*; e1-e2 ->e1(x)-e2(x)=0 ->e1(x)=e2(x)

Доказано.

Теорема «О порождающей матрице циклического кода»: Пусть С – циклический код над с длинной кодового слова и порождающим многочленом . Тогда в качестве порождающей матрицы кода С можно взять матрицу вида:

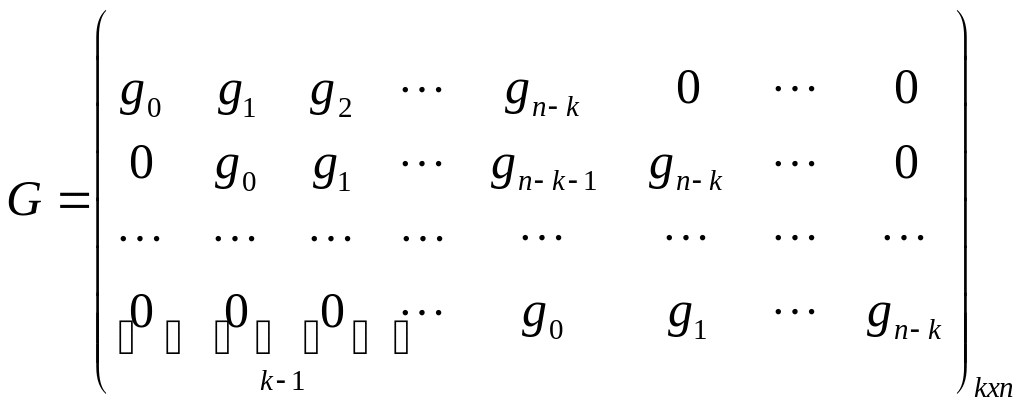
Доказательство: Для доказательства теоремы необходимо и достаточно показать, что вектора:

, , являются базисом кода С.

Запишем многочлены, которые соответствуют данным кодовым словам:

; ;

Так как код С является идеалом, порожденным многочленом , то

Покажем, что элементы - линейно независимы. Рассмотрим линейную комбинацию:

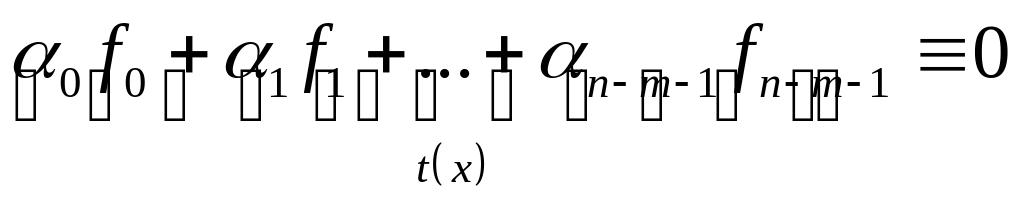
Заметим, что многочлен имеет степень не большую, чем , т.к. этот многочлен тождественно равен нулю в кольце . Значит мы можем сказать, что все коэффициенты указанной линейной комбинации равны 0. Запишем равенство коэффициентов нулю в виде системы:

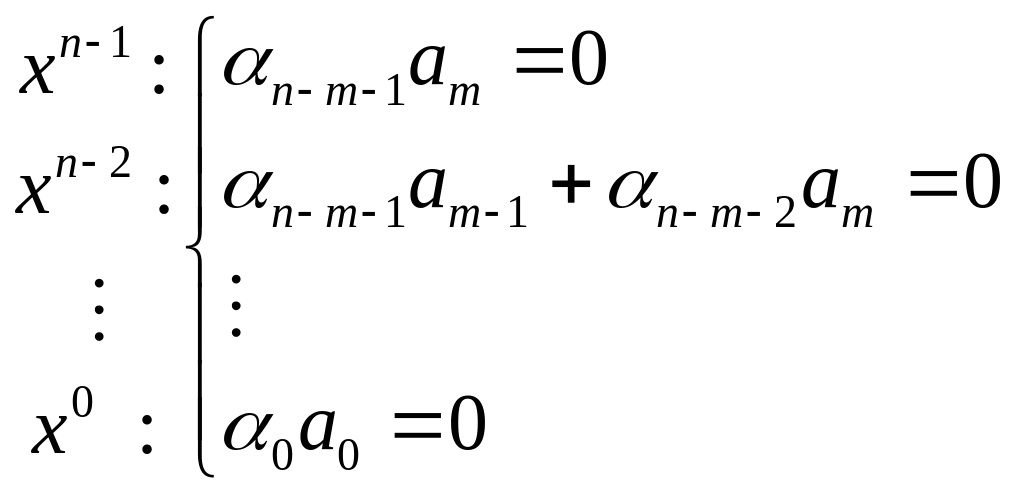
Поскольку , то . Из второго уравнения: . И так далее до . Таким образом, мы показали, что система линейно независима. Покажем, что данная система является полной в С. Возьмем произвольный многочлен . можно выбрать таким образом, что бы он представлялся в виде: , где . Но тогда имеет вид: , где . Следовательно: . Таким образом матрица действительно порождающая матрица. Следствие: Пусть циклический код С с длинной кодового слова и порождающим многочленом , таким что: . Тогда .

Теорема «О проверочной матрице циклического кода»: Пусть циклический код С с длинной кодового слова и проверочным многочленом , . Тогда в качестве проверочной матрицы кода С можно взять матрицу вида:

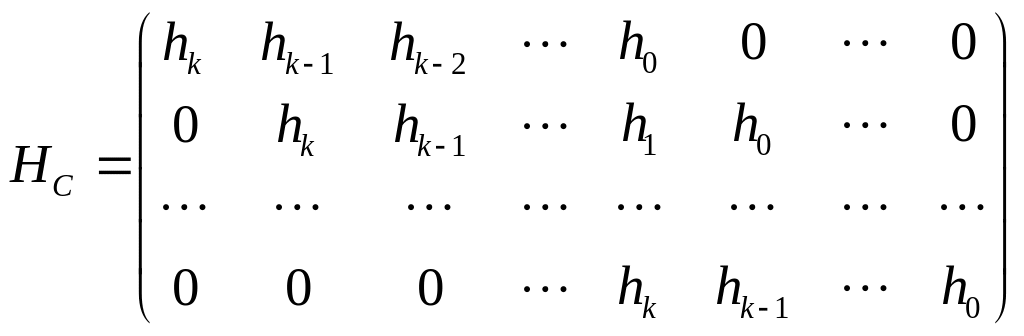Д оказательство: Т.к. проверочный многочлен , где - порождающий многочлен, то:

в кольце . В самом деле: в кольце, так как С – идеал. Если делится нацело на . Следовательно: . Приравнивая к нулю коэффициенты при соответствующих степенях в произведении , получим систему линейных уравнений с матрицей вида:

М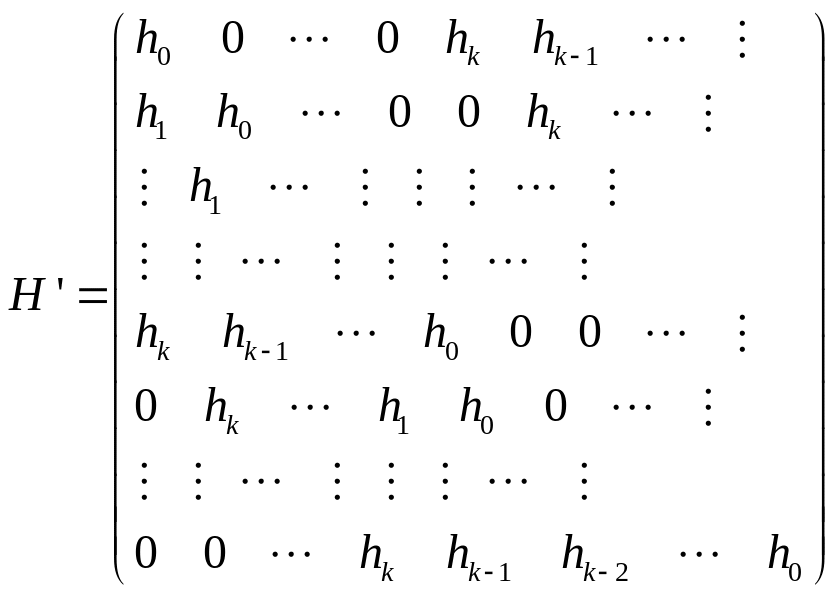 атрица будет являться одной из проверочных матриц для кода С. Из соображений размерности получим: . Легко заметить, что последнее строк матрицы линейно независимы, поэтому предыдущие строки можно отбросить и получить в качестве проверочной матрицы матрицу Н из условия теоремы.

20