18. Математическая модель канала связи.

Опр.: Канал называется дискретным по входу (выходу), если множество входных (выходных) сигналов конечно. Канал называется с дискретным временем, если сигналы на входе и выходе представляют собой конечные или бесконечные последовательности элементов алфавита Х на входе канала и алфавита Y на выходе. Дискретный по входу и выходу канал с дискретным временем будем называть дискретным каналом.

Опр.: Дискретный канал называется каналом без памяти (ДКПБ) если для любого n и любых последовательностей и имеет место равенство:

. Дискретный канал без памяти (ДКБП) обозначается как , где X и Y – входные и выходные алфавиты, а - переходные вероятности канала.

Опр.: Кодом длинны n и объемом М для канала называется множество из М пар , где последовательности длины n, образованные входными сигналами канала и называемые кодовыми словами , и - решающие области, образованные выходными последовательностями канала, причем при множества и не пересекаются.

Если решающие области заданы, то декодирование выполняется след образом: если y принадлежит А_i, то декодируем y в U_i

Опр.: Скоростью кода (или скоростью передачи) называется величина , где M – объем кода, n - его длинна. Скорость кода представляет собой максимальное количество информации, которое может быть передано с помощью одного сигнала (символа кода). Такое количество информации передается по каналу, если кодовые слова имеют одинаковую вероятность появления. Скорость кода измеряется в битах на символ.

Опр.: Пропускной способностью канала называется максимальное число С, такое что для любого сколь угодно малого и любого R, R<C существует код G(n,R) такой, что средняя вероятность ошибки удовлетворяет неравенству . где - средняя вероятность ошибки декодирования.

Опр. - вероятность ошибки декодирования i-го кодового слова. 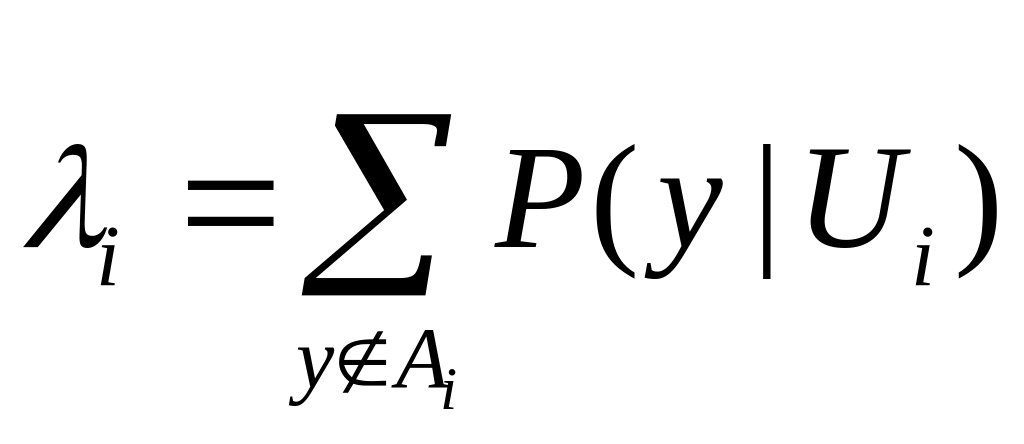. Средняя вероятность ошибки декодирования . Если известно распределение вероятностей кодовых слов на входе канала p(U), тогда

Опр.: Информационная емкость С* дискретного канала без памяти определяется соотношением: , где максимум берется по всем входным распределениям вероятностей p(x) на X.

I(X, Y) - взаимная информация источников X и Y. MI(*,*) = I(X, Y), где *- фиксир. элемент из соотв. множества.

I(X,Y)=0 <=> источники X и Y независимы. I(X,Y) =H(Y) - H(Y|X) = H(X) - H(X|Y)/

Для двоично симметричного канала С*= 1 - h(p), h(p)=plog(1/p) + (1-p)log(1/(1-p));

Формулировка теоремы Шеннона о кодировании в канале:

C = C*.

Словами: пропускная способность канала равна информационной емкости канала.

19. Линейные коды. Порождающая матрица линейного кода, проверочная матрица. Минимальное кодовое расстояние, теорема Хемминга. Синдромное декодирование. Код Хэмминга, декодирование кодов Хемминга.

• Линейные коды. Порождающая матрица линейного кода, проверочная матрица.

Линейным кодированием называется отображение , удовлетворяющее требованиям:

1. - линейное отображение ( , )

2. - инъективно (разные элементы множества X переводятся в разные элементы множества Y).

Пусть - линейное кодирование, тогда линейным кодом соответствующим кодированию называется множество (образ )

Заметим, что линейный код является подпространством пространства , а т.к. - инъективно, то размерность .

Пусть - линейное кодирование, тогда порождающей матрицей линейного кода С, соответствующего называется матрица отображения в стандартных базисах:

В столбцах порождающей матрицы записаны координаты образов базисных векторов пространства и следовательно столбцы этой матрицы образуют базис кода С как векторного пространства. Линейные коды в пространстве - это в точности все возможные подпространства данного пространства. Если задан какой либо линейный код, то он может соответствовать различным линейным кодированиям, соответственно имеет различные порождающие матрицы.

Обозначение: если С – это подпространство размерности k пространства , то будем говорить что С является (n, k) кодом. Где длинна кода, а - его размерность

Пусть С - линейный (n, k) код над полем , тогда матрица с элементами из называется проверочной матрицей для кода С, если выполняются следующие условия:

1. (количество столбцов в равно )

2. 

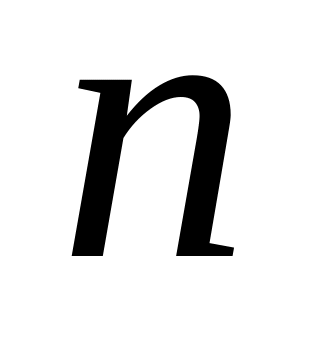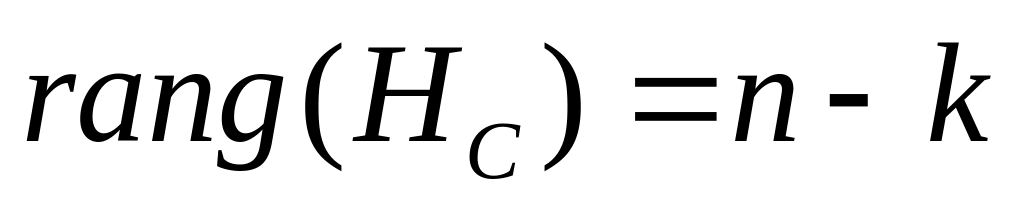
Теорема о связи порождающей и проверочной матрицы.

Пусть С – линейный (n,k) код, , - его порождающие и проверочные матрицы. Тогда будут справедливы следующие утверждения:

1. (нулевая матрица)

2. Если матрица имеющая размерность с элементами из , удовлетворяет условию 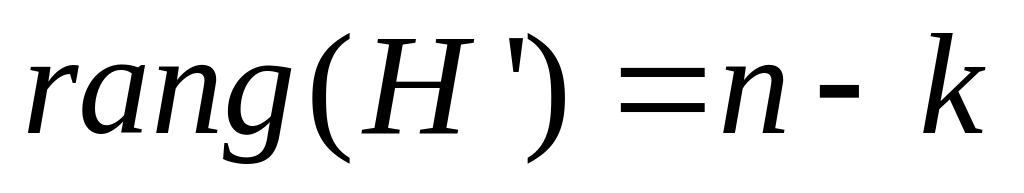такова что 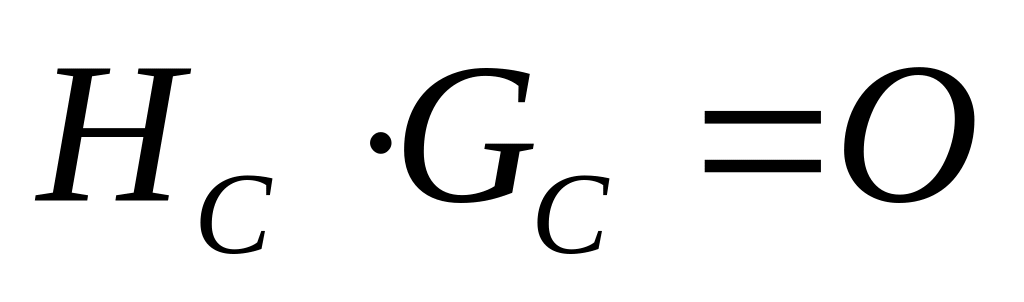, то будет являться проверочной матрицей для кода С

Теорема о проверочной матрице

Пусть С- (n,k) код, и d_min = d;

1. d>=S+1 <=> любые s столбцов проверочной матрицы линейно независимы

2. d<=n-k +1(теорема Синглтона)

3.d=n-k+1 <=> любые n-k столбцов лиейно независимы.

Доказательство:

1. =>: Пусть d>=S+1 и пусть найдутся <=S линейно независимых столбцов в матрице H. Значит существует вектор с' , w(c')<=S т.ч. H*c'=0 ->d_min = d <=S противоречие.

<=:

Существует вектор с', т.ч. H*c'^t = 0; ->d_min=d <=s

Пусть 0<w(c')<=S. 0= H*c't= - сумма не более чем S столбцов матрицы H. Существует не более чем S линейно зависимых столбцов, по условию они линейно независимы, тогда получим нулевую комбинацию с ненулевыми коэффициентами, тогда выполняется w(c')>=S+1, значит d_min=min(w(c'))>=S+1

2.согласно доказанному утверждению d не может быть > n -k +1; если это так то любые n-k+1 будут независимы, это не возможно т.к. rangH=n-k, т.е. любые n-k+1 столбцов линейно зависисмы

3. d=n-k+1 - любые n-k столбцов линейно независимы - больше быть не может.

Доказано.

Одну через другую можно найти следующим образом:

G=[E_k :P]; H= [P^t : E_n-k]

• Минимальное кодовое расстояние, теорема Хемминга.

Опр. Определим расстояние Хемминга на следующим образом по правилу d(x,y) = количеству координат, по которым x и y отличаются.

Теорема о свойствах расстояния Хемминга

Расстояние Хемминга над является метрикой, т.е. для него выполнены аксиомы:

1. (положительная определенность)

2. (симметричность)

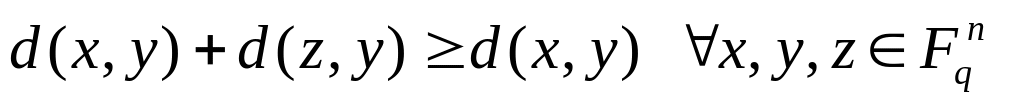3. (неравенство треугольника)

Опр. Весом Хемминга элемента называется число

Свойства веса Хемминга: 1) ; 2)

Теорема о декодировании по принципу максимальной вероятности

Пусть С - код над . Предположим, что все кодовые слова могут с одинаковой вероятностью встречаться в отправленном сообщении. Предположим, что в результате передачи некоторого кодового слова из С по информационному каналу было получено сообщение . Тогда наиболее вероятным будет следующее событие: отправлено сообщение

Опр. Пусть С – линейный код в , тогда минимальным кодовым расстоянием данного кода будет называться число

Замечание: Тогда по свойству расстояний Хемменга несложно заметить закономерность, характерную только для линейных кодов: .

Опр.: Будем говорить, что код С обнаруживает ошибок, если любое сообщение, содержащее ошибок ( ), будет интерпретировано получателем как ошибочное.

Опр.: Будем говорить, что код С исправляет ошибок тогда и только тогда, когда любое сообщение, содержащее ошибок ( ), будет декодировано верно.

Пример: Рассмотрим код с повторением , т.е.

Код позволяет обнаружить две ошибки, а исправляет одну.

Пример: Рассмотрим код с проверкой на четность: , т.е. . Указанный код обнаруживает одну ошибку. Не исправляет ни одной.

Теорема «О связи минимального расстояния с количеством обнаруживаемых и исправляемых ошибок»: Пусть С – код в (не обязательно линейный) и , тогда данный код обнаруживает ошибку, а исправляет ( целая часть ) ошибок. Доказательство:

1. Предположим, что было получено сообщени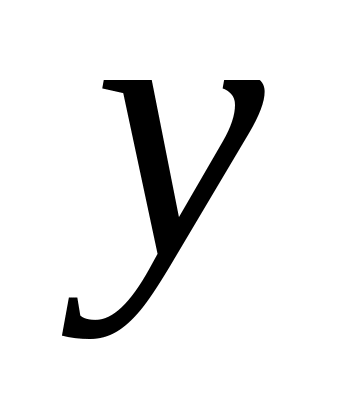е , содержащее ошибок, где , а отправлено сообщение , т.е. . Т.к. кодовое слово, а , то не может быть кодовым словом. Следовательно, ошибочное сообщение.

2. Покажем теперь, что данный код исправляет указанное количество ошибок. Пусть отправлено , а получено , содержащее ошибок, где .

От противного.Пусть декодировано неверно.Это возможно если , но тогда справедливо: . Получили противоречие с определением минимального расстояния.

• Синдромное декодирование

Опр. Пусть - проверочная матрица линейного кода в . Пусть , тогда синдромом вектора y называется вектор столбец, вычисленный по правилу

S(y)=y*H^t

Свойства синдрома:

1) 2) 3)

4) (равенство смежных классов)

Опр. Пусть , тогда x называется лидером множества M, если он имеет минимальный вес Хемминга

Утверждение о ближайшем соседе

Пусть С – линейный код в , - проверочная матрица, , тогда будет ближайшим к элементу y в смысле расстояния Хемминга элемент будет лидером смежного класса с синдромом S(y)

Алгоритм декодирования с помощью синдромов и лидеров

1. Найти проверочную матрицу

2. Перечислить все смежные классы по С и для каждого смежного класса указать соответствующий ему синдром и выбрать какого-либо лидера этого класса.

3. Для полученного сообщения вычислить его синдром

4. По полученному синдрому найти соответствующий этому синдрому лидер z

5. Декодировать , где

Пример ,

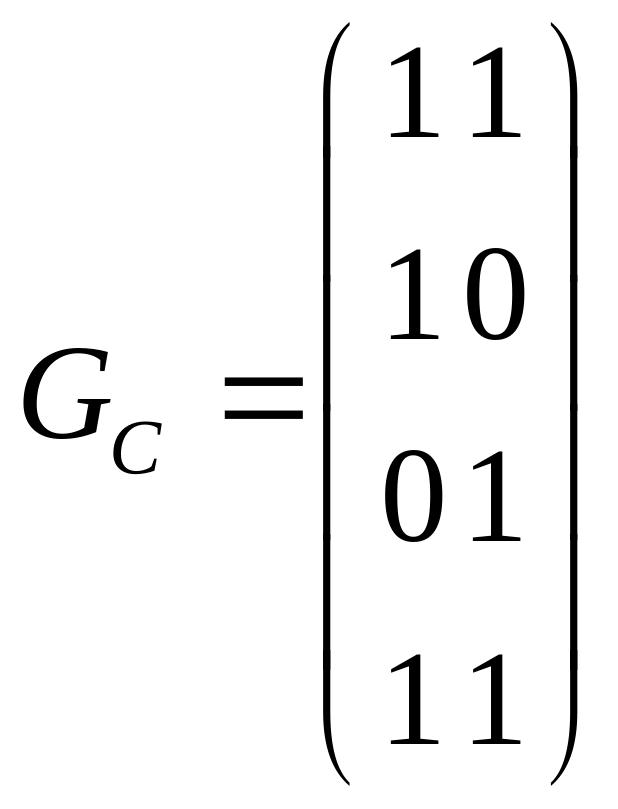1. Поиск по : а) записать слу б) Найти фундаментальную систему решений; в) вектора фунд. сист. Решений записать в строки проверочной матрицы

2. 

(лидеры подчеркнуты, в 3м классе смежности 2 лидера, значит декодирование неоднозначное)

3. Лидер – Синдром

4. . Соответствует лидеру

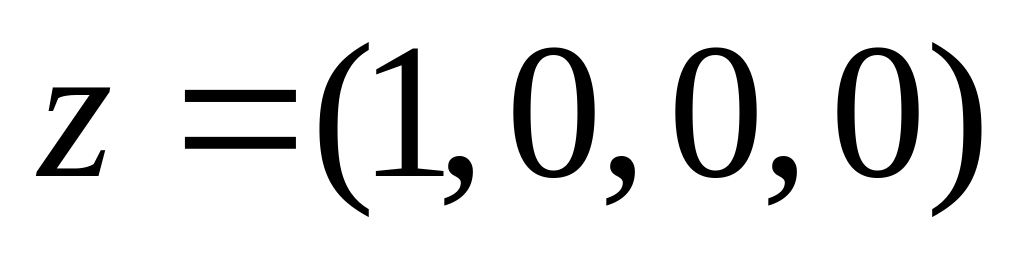
5. Декодирование:

• Код Хэмминга, декодирование кодов Хемминга

Опр. Пусть ( ), тогда кодом Хемминга с параметром m называется бинарный код, проверяющая матрица которого состоит из всех ненулевых различных бинарных столбцов высоты m.

Замечание. Обычно в качестве проверочной матрицы кода Хемминга берут упорядоченную проверочную матрицу , у которой в i-ом столбце содержится бинарная запись числа i.

n=2^m-1; k=2^m-m-1. (n, k) - код Хэмминга

Пример. ,

Теорема о коде Хемминга

Пусть код Хемминга с параметром m, тогда справедливо:

1) 2) - совершенный код, исправляющий 1 ошибку

((n, k) код совершенный, если в границе Хемминга для него достигается равенство: )

Декодирование кодов Хемминга

Предположим, что нам требуется декодировать сообщение , если известно, что было отправлено кодовое слово принадлежащее коду Хемминга с параметром m.

Т.к. С_m это совершенный код, исправляющий 1 ошибку, то для сообщения y т.ч .

Поэтому . Представим , где , где е – вектор ошибок.

Пусть - упорядоченная проверочная матрица. Вычислим синдром y, относительно этой матрицы. ( )

Случай 1. Если

Случай 1. Если 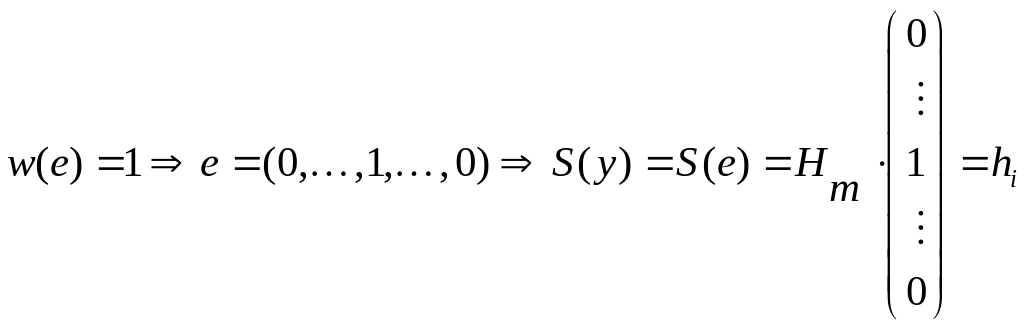i – столбец матрицы

В упорядоченной матрице i-ый столбец содержит бинарную запись числа i S(y) – бинарная запись номера той координаты в которой произошла ошибка.

Алгоритм декодирования:

1. Вычислить S(y) относительно упорядоченной матрицы

2. По виду S(y) определить номер координаты, в которой произошла ошибка (S(y)-бинарная запись этого номера)

3. Изменить координату, в которой произошла ошибка на ее отрицание

Пример Декодировать сообщение , если оно принадлежит

1)

2)100 – запись числа 4, N=4, значит меняем 4ю координату. 3)