
- •Высшая математика
- •Введение
- •Глава I. Неопределенные и определенные интегралы
- •1.Неопределенный интеграл
- •Непосредственное интегрирование.
- •Интегралы вида .
- •Интегралы вида
- •Основные методы вычисления определенных интегралов
- •Формула Ньютона – Лейбница.
- •2.Замена переменной в определенном интеграле.
- •Интегрирование по частям в определенном интеграле.
- •3. Несобственные интегралы
- •4. Приложения определенных интегралов
- •Глава 2. Дифференциальные уравнения
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка. Уравнение Бернулли
- •3. Дифференциальные уравнения, допускающие понижение порядка Уравнение вида .
- •Уравнение вида .
- •4. Линейные дифференциальные уравнения - го порядка.
- •5. Системы дифференциальных уравнений
- •Глава 3. Дифференциальное исчисление функций многих переменных
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Предел и непрерывность функции
- •Частные производные. Дифференциал функции
- •Производная в данном направлении. Градиент
- •Экстремумы функции нескольких переменных
- •Оглавление
- •Глава I. Неопределенные и определенные интегралы………….…3
- •3. Несобственные интегралы ……………………………………………….15
- •4. Приложения определенных интегралов ………………………………...17
- •Глава II. Дифференциальные уравнения ……………………………...18
- •Глава III. Дифференциальное исчисление функций многих переменных ……………………………………………………………………31
Глава 3. Дифференциальное исчисление функций многих переменных
Теоретические вопросы
1. Определение функции многих переменных.
2. Предел и непрерывность функции многих переменных.
3. Частные производные.
4. Дифференциал функции.
5. Производная по направлению. Градиент.
6. Касательная плоскость и нормаль к поверхности.
7. Экстремум функции нескольких переменных.
Литература
1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.: Высш. шк., 1998. Ч. 1,2.
1. Основные понятия
Пусть
![]() -
произвольное множество точек n
- мерного арифметического пространства.
Если каждой точке
-
произвольное множество точек n
- мерного арифметического пространства.
Если каждой точке
![]() поставлено в соответствие некоторое
действительное число
поставлено в соответствие некоторое
действительное число
![]() ,
то говорят, что на множестве
,
то говорят, что на множестве
![]() задана функция
задана функция
![]() от
n
переменных
от
n
переменных
![]() .
Множество
называется областью
определения,
а множество
.
Множество
называется областью
определения,
а множество
![]() -
областью
значений функции
-
областью
значений функции
![]() .
В частном случае, если n=2,
имеем функцию двух переменных:
.
В частном случае, если n=2,
имеем функцию двух переменных:
![]() .
.
2. Предел и непрерывность функции
Число
![]() называется пределом
функции
называется пределом
функции
![]() при
при
![]() ,
если для любого числа
,
если для любого числа
![]() найдется такая
найдется такая
![]() -
окрестность
точки
-
окрестность
точки
![]() :
:
![]() ,
что для любой точки
,
что для любой точки
![]() из этой окрестности имеет место
неравенство:
из этой окрестности имеет место
неравенство:
![]() .
.
Записывают этот факт следующим образом:
![]() .
(1)
.
(1)
Заметим, что свойства пределов и действия над пределами для функции многих переменных аналогичны свойствам пределов и действиям над пределами для функции одной переменной.
Функция
называется
непрерывной в точке
![]() ,
если:
,
если:
1)
![]() ;
;
2)
![]() .
(2)
.
(2)
Свойства непрерывных функций многих переменных и действия над непрерывными функциями многих переменных аналогичны свойствам непрерывных функции одной переменной и действиям над непрерывными функциями одной переменной.
Точка называется точкой разрыва непрерывности функции , если в этой точке функция не является непрерывной, т.е. если нарушено хотя бы одно из условий определения непрерывности.
Частные производные. Дифференциал функции
Частной производной функции по переменной в точке называется предел:
![]() ,
(3)
,
(3)
где
![]() -
приращение аргумента
.
Аналогично определяется частная
производная функции
по переменной
в точке
:
-
приращение аргумента
.
Аналогично определяется частная
производная функции
по переменной
в точке
:
![]() ,
(4)
,
(4)
где
![]() -
приращение аргумента
.
Частные производные функции
по переменной
обозначают различными способами,
например:
-
приращение аргумента
.
Частные производные функции
по переменной
обозначают различными способами,
например:
![]()
Аналогично частные производные функции по переменной обозначают следующим образом:
![]()
Заметим, что в силу определения частной производной все правила и формулы дифференцирования, введенные для функции одной переменной, сохраняются. Следует лишь помнить, что во всех этих правилах и формулах при нахождении частной производной по какому-либо аргументу все остальные аргументы считаются постоянными.
Частные производные
![]() и
и
![]() функции
также являются функциями двух переменных
и
.
Поэтому эти функции, в свою очередь,
могут иметь частные производные, которые
называются частными
производными второго порядка
исходной
функции
и обозначаются следующим образом:
функции
также являются функциями двух переменных
и
.
Поэтому эти функции, в свою очередь,
могут иметь частные производные, которые
называются частными
производными второго порядка
исходной
функции
и обозначаются следующим образом:
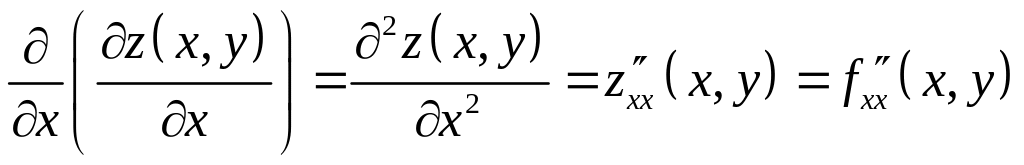 - вторая
частная
производная
функции
по переменной
;
- вторая
частная
производная
функции
по переменной
;
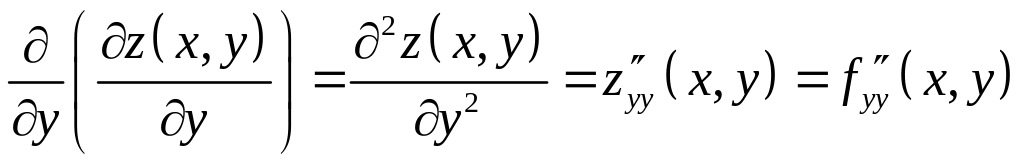 -
вторая частная
производная
функции
по переменной
;
-
вторая частная
производная
функции
по переменной
;
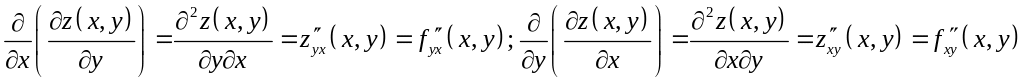 -
смешанные
производные второго порядка функции
.
-
смешанные
производные второго порядка функции
.
Выражение
![]()
называется полным приращением функции в точке , а выражение
![]()
- полным дифференциалом функции .
Аналогичные
формулы имеют место и для функции трех
переменных
![]() .
.
Задание.
Показать, что функция
![]() удовлетворяет уравнению:
удовлетворяет уравнению:
![]() .
.
Решение. Найдем соответствующие частные производные, входящие в данное уравнение:
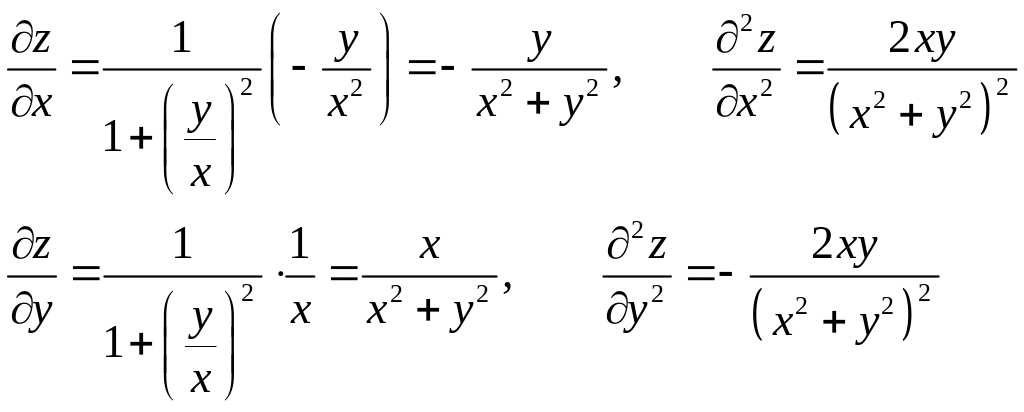
Подставим полученные значения частных производных второго порядка от функции в исходное уравнение. Получим:
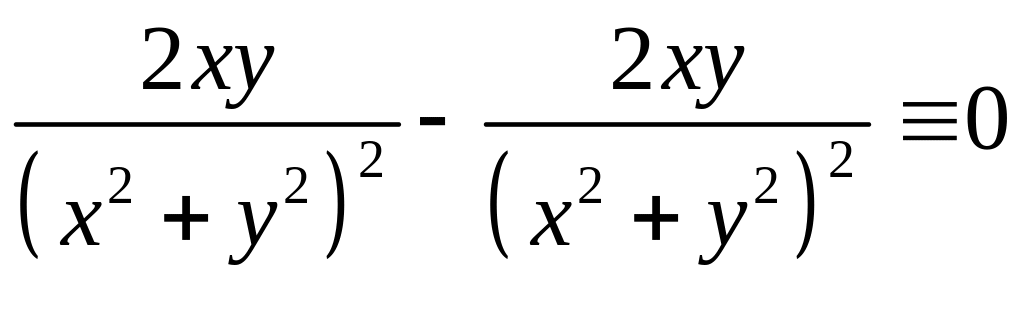 .
.
Следовательно, функция удовлетворяет данному уравнению.
