§5 Замена переменных в двойном интеграле.

При вычислении двойного интеграла часто применяется метод подстановки, то есть совершается преобразование переменных .

Пусть совершена подстановка

где и - новые независимые переменные. Эти функции имеют непрерывные частные производные. С помощью этих функций каждая т. обл. D в пл. xoy отображается в т. обл пл. .

При этом отображении внутренние точки отображаются во внутренние, а граничные в граничные.

При этом отображении элементарная площадь 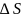преобразуется в элементарную площадь , получается следующая формула преобразования переменных в двойном интеграле:

где - якобиан перехода и вычисляется по формуле

Рассмотрим двойной интеграл в полярной системе координат.

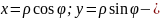
– формулы связывающие декартовы координаты с полярными.

Пример: Вычислить двойной интеграл

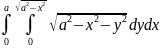
Построим обл. D: x=0 x=a

y=0 y=

Преобразуем интеграл перейдя к полярным координатам

y= - окружность

в полярных координатах

6. Вычисление площадей и объёмов с площадью двойных интегралов.

Нам известно уже, что объём тела, ограниченного поверхностью z= f(x, y), где f(x, y)≥0, пл. z=0 и цилиндрической поверхностью, образующие которой параллельны оси OZ, а направляющей служит граница.

Объем V вычисляется по формуле:

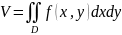
Если тело ограничено поверхностям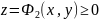и:

и ,

п ричем ,

то обём тела равен разности объёмов тел, ограничено поверхностью ,

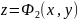а  .

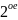
Поэтому объём тела будет равен:

или

Пример: Вычислить объём тела, ограниченного поверхностями

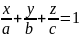, x=0, y=0, z=0

Построим это тело

Тело ограничено координатами плоскостями и пл.

y

b

D

0

a

0

x

Сверху тело ограничено плоскостью

;

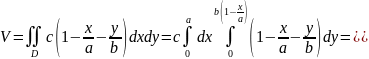
Замечание: Если ф – ия f(x, y) в обл. D меняет знак, то обл. D разбиваем на части:

а) обл. , где f(x, y)≥0

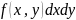
б) обл. , где f(x, y)<0

Тогда:

Вычислим площадь плоской обл. D

Пусть функция f(x,y)≡1 в обл. D,

тогда интегральная сумма для двойного интеграла будет иметь вид

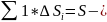площадь обл. D.

т

.е.

Пример: Вычислить площадь фигуры, ограниченной линиями

Из ;

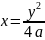0≤ y ≤ 2a Из ;

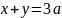
§7 Тройной интеграл, масса неоднородного тела.

Пусть в декартовой системе координат oxyz дано неоднородное тело Т, ограниченное замкнутой поверхностью S, его объём V, и пусть переменная плотность f(x,y,z) тела Т – есть непрерывная функция. Требуется вычислить массу m этого тела Т.

Разобьём это тело Т на n элементарных тел , объемом . Выберем в каждом элементарном теле произвольную т. и предположим что плотность f( ) – постоянна для всех т. тела . Тогда масса тела будет равна f( )* ,

а масса всего тела Т будет:

У

1

величивая число разбиений n, мы неограниченно уменьшаем объём тела и сумма имеет определённый предел при max Этот предел принимается за точную величину массы тела Т:

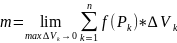
Эта сумма – есть интегральная сумма для функции f(x,y,z) по обл.V.

О

1

пределение: Тройным интегралом от функции f(x,y,z) по замкнутой трёхмерной обл. V называют предел интегральной суммы когда наибольший объём элементарной обл. :

или