Тема 7. Решение игры в смешанных стратегиях

Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение

называется ценой игры в смешанных стратегиях, а стратегии и для которых выполняются равенства

(и тогда это общее значение равно ), называются оптимальными смешанными стратегиями соответственно игроков А и В.

Таким образом, оптимальные смешанные стратегии и (которые, в частности, могут быть и чистыми) обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии.

Нетрудно показать, что

т. е. цена игры в смешанных стратегиях V не меньше нижней цены игры в чистых стратегиях а и не больше верхней цены игры в чистых стратегиях .

Полным решение игры в смешанных стратегиях называется совокупность множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий и цена игры V образуют частное решение в смешанных стратегиях.

Основная теорема теории игр, сформулированная и доказанная фон Нейманом¹, устанавливает существование решения любой конечной матричной игры.

Теорема 7.1 (основная теорема матричных игр фон Неймана). Любая матричная игра имеет решение в смешанных стратегиях, т. е. существуют цена игры в смешанных стратегиях V и оптимальные смешанные стратегии и соответственно игроков А и В, т. е.

Теорема 7.2 (свойство равнозначности седловых точек). Если и - седловые точки функции на декартовом произведении , то значения данной функции в этих точках совпадают:

Теорема 7.3 (критерий существования седловой точки). Для того чтобы функция , , , имела седловую точку на декартовом произведении , необходимо и достаточно, чтобы существовали

и

и выполнялось их равенство

Пример 7.1. Пусть и , т.е. х и у - скалярные переменные, и точки и , которые графически изображаются двумя вершинами прямоугольника (см. рис. 7.1), являются седловыми точками функции . Тогда по свойству взаимозаменяемости, сформулированному в теореме 9.3, остальные две вершины этого прямоугольника и также являются седловыми. В связи с этим иногда свойство взаимозаменяемости седловых точек называют свойством "прямоугольности".

Если, в частности, , то точки , лежат на одной вертикали , а если , то эти точки лежат на одной горизонтали ; поэтому в этих случаях взаимозамена неравных координат этих точек приводит к паре тех же точек и прямоугольник вырождается в отрезок.

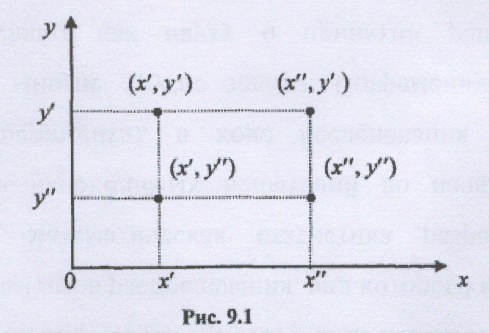
Рис. 7.1

Пример 9.3. Применяя критерий (теорема 9.4), определить, существует ли у функции

на декартовом квадрате [0,1]² седловые точки.

Решение. Очевидно, что

при любом ,

и, следовательно,

Также очевидно, что

, при любом

и потому

.

Итак, имеем

т.е. выполняются необходимые условия и потому на квадрате [0,1]² существуют седловые точки.

Тема 8. Критерии и свойства оптимальных стратегий

Теорема 8.1. Пусть V- цена игры, - функция выигрыша, За и - множества смешанных стратегий соответственно игроков А и В.

1. Для того чтобы стратегия игрока А была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство

для любого

т.е. выбор игроком А оптимальной стратегии гарантирует ему выигрыш , не меньший цены игры V, при любой стратегии игрока В.

2. Для того чтобы стратегия игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство

для любого ,

т. е. выбор игроком В одной из своих оптимальных стратегий гарантирует ему проигрыш, не больший цены игры У, при любой стратегии Р игрока А.

Теорема 8.2. Пусть V - цена игры, - функция выигрыша, и - множества чистых стратегий соответственно игроков А и В.

1. Для того чтобы стратегия игрока А была оптимальной, необходимо и достаточно, чтобы

2. Для того чтобы стратегия игрока В была оптимальной, необходимо и достаточно, чтобы

Пример. Рассмотрим матричную игру с платежной матрицей

А=
		0
		1

и смешанные стратегии и соответственно игроков А и В. В упражнении 9.2 было отмечено, что из примера 8.3 по теореме фон Неймана следует оптимальность стратегии и . Установим этот факт на основании теоремы 8.2.

Имеем, что цена игры .

Получаем следующие значения функции выигрыша:

Таким образом, и потому по достаточной части утверждения 1 теоремы 8.2 (см. (10.10)) стратегия является оптимальной стратегией игрока А.

Также имеют место неравенства , (которые на самом деле являются равенствами) и, следовательно, по достаточной части утверждения 2 теоремы 8.2 стратегия является оптимальной стратегией игрока В.

Пусть оптимальная смешанная стратегия игрока А. В общем случае, некоторые из вероятностей могут быть равными нулю. Если , где i - одно из чисел , то в оптимальной смешанной стратегии чистая стратегия не участвует и потому называется пассивной. Чистые стратегии , входящие в оптимальную стратегию Р° с положительной вероятностью , называются активными стратегиями игрока А. Таким же образом определяются активные стратегии игрока В. Понятно, что оптимальная чистая стратегия является активной. Следующая теорема об активных стратегиях играет существенную роль в решении игр.

Теорема 8.3(об активных стратегиях). Пусть V- цена игры, и - оптимальные стратегии соответственно игроков А и В. Тогда справедливы следующие утверждения.

1. Для любой активной стратегии игрока А выполняется равенство

.

2. Для любой активной стратегии игрока В выполняется равенство

.