3) «118» Общее решение линейного неоднородного уравнения высшего порядка

Теорема. Общее решение неоднородного линейного дифференциального уравнения высшего порядка состоит из суммы его частного решения и общего решения соответствующего однородного уравнения.

Билет №19

1. «56» Неопределенные выражения. Первый и второй замечательные пределы

2. «74» Асимптоты графика функции (вертикальная, горизонтальная, наклонная)

3. «113» Линейные уравнения первого порядка. Уравнения Бернулли

«114» Уравнения в полных дифференциалах. Теорема Коши

4. Теория вероятности

«56» Неопределенные выражения. Первый и второй замечательные пределы

Неопределённые выражения в математике, выражения, предел которых не может быть найден путём непосредственного применения теорем о пределах.

Неопределённые выражения:

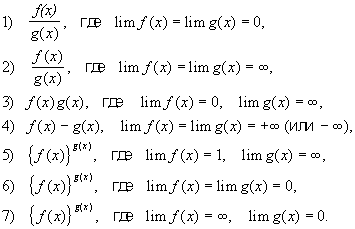Первый замечательный предел

Второй замечательный предел

2)«74» Асимптоты графика функции (вертикальная, горизонтальная, наклонная

Определение.Асимптотой графика функцииy=f{x) называется прямая, обладающая тем свойством, что расстояние от точки (х, flx))до этой прямой стремится к нулю при неограниченном удале­нии точки графика от начала координат:

На рис. 8.20а изображена вертикальная асимптота, на рис. 8.206 — горизонтальная асимптота, а на рис. 8.20в — наклонная.

Теорема 1. Пусть функция у =f(x)определена в некоторой окрест­ности точки Xо(исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х→x₀ - 0 (слева) или при х→х₀ +0 (справа) равен бесконечности, т.е. Iimf(x)= ∞ илиIimf(x)= ∞.

х→x0 – 0 х→х0 +0

Тогда прямая х =x₀является вертикальной асимптотой графика функции у=f(х).Вертикальную асимптоту следует искать в точках разрыва функции или на концах её области определения (а,b), если а, b – конечные числа.

Теорема 2. Пусть функция у =f(х) определена при достаточно больших х и существует конечный предел функцииlimf(x)=b; х→∞

Тогда прямая у =b есть горизонтальная асимптота графика функцииy=f(x)

Замечание. Если конечен только один из пределов limf(x)= b_nили limf(x)=b_п, то функция имеет лишь х→-∞ х→+∞

левостороннююу = b_я илиправостороннюю у=b_п-горизонтальную асимптоту.

В том случае, если limf(x)=cо, функция может иметь наклонную асимптоту х→∞

Теорема 3.Пусть функция у=f(х) определена при достаточно боль­ших х и существуют конечные пределыlim=f(x) и lim[f(x)- х→∞x

кх] =b.Тогда прямая у=кх±b является наклонной асимптотой гра­фика функции y=fix).Наклонная асимптота, так же,как и горизонтальная , может быть правосторонней или левосторонней

3. 113» Линейные уравнения первого порядка. Уравнения Бернулли «114» Уравнения в полных дифференциалах. Теорема Коши

Уравнение вида a(x)y' + b(x)y + c(x) = 0 или y' + p(x)y + q(x) = 0, где a(x), b(x), c(x), p(x), q(x) – непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Метод решения уравнения Бернуллиy' + p(x) y = q(x) yⁿ: где p(x), q(x) – непрерывные функции. Вводим новую функцию z(x)=y^1-n, тогда z'=(1-n)*y^-n*y'. Разделим обе части исходного уравнения на yⁿ: y^-ny' + p(x) y^1-n= а(x). Теперь переходим к новой функции (умнож. на (1-n)): z' + (1-n)*p(x)*z = (1-n)*q(x). Получили линейное уравнение отн. функции z(x), его метод решения неизв

Коши: Уравнение M(x,y)*dx + N(x,y)*dy = 0 называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции F(x,y). Это имеет место, если ∂M/∂y≡∂N/∂x.Метод решения: чтобы решить уравнение в полных дифференциалах, надо найти функцию F(x,y), для которой полный дифференциал равен левой части уравнения: dF(x,y) = M(x,y)*dx + N(x,y)*dy. Тогда общее решение исходного уравнения можно записать в виде F(x,y) = C, где С – произвольная постоянная. Для этого равенство d/dxF(x,y) = M(x,y). Интегрируем по переменной x, полагая при этом y постоянным, получаем F(x,y) = ∫M(x,y)dx + φ(y). Дифференцируя по y и приравнивая к N(x,y) получаем: d/dyF(x,y) = d/dy(∫M(x,y)dx) + N(x,y) φ(y) = -∫(d/dy∫M(x,y)dx)dy + ∫N(x,y)dy. F(x,y) = ∫M(x,y)dx - ∫(d/dy∫M(x,y)dy + ∫N(x,y)dy.Теорема Коши: пусть функция f(x,y,y') и её частные производные f'_y и f'_x непрерывны в некоторой области G пространства переменных (x,y,y'). Тогда для любой внутренней точки M₀(x₀,y₀,y'₀) этой области существует единственное решение уравнения вида y''=f(x,y,y'), удовлетворяет начальным условиям: x≠0; y=x₀; y'=y'₀

Билет №20

1. «93» Полный дифференциал функции нескольких переменных. Производная сложной функции

2. «133» Математическое ожидание, основные свойства

3. «1» Множества. Операции над множествами. Круги Эйлера

4. Исследовать сходимость ряда