7. Интегральное представление частичной суммы тригонометрического ряда Фурье. Теорема о сходимости ряда Фурье.

Интегральное представление частичной суммы тригонометрического ряда Фурье.

Рассмотрим функцию f(x) с периодом 2π и кусочно-непрерывную на любом конечном промежутке. Тогда ей можно сопоставить ряд Фурье:

(1), где k=0,1,2…, и k=1,2,…. Запишем 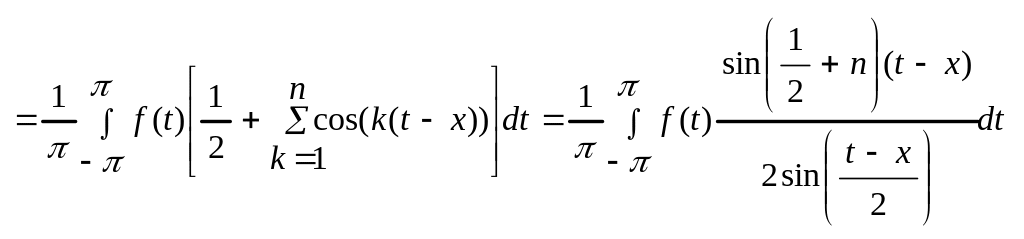. Получили интегральное представление. Сделаем замену t-x=z: 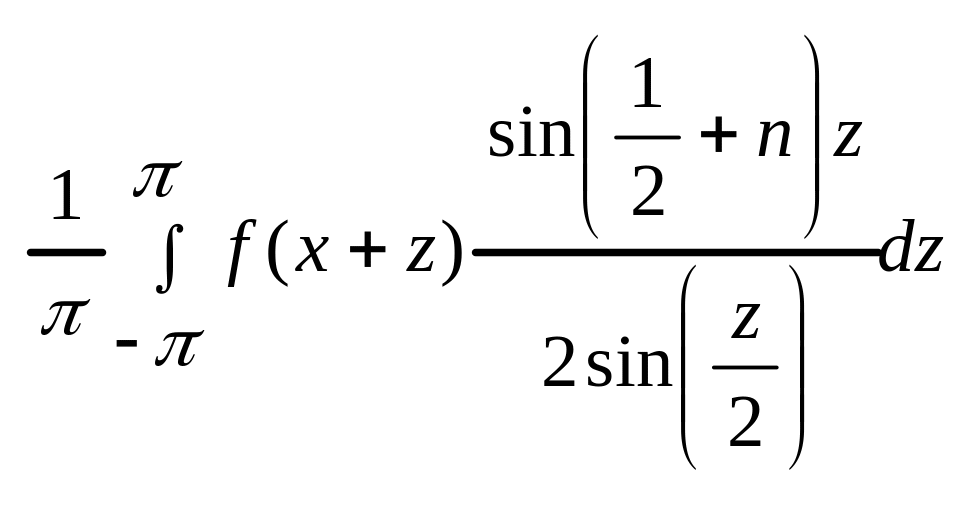. Т.о. = (разбивая промежуток [-π,π] на два: [-π,0] и [0,π] и меняя z на –z ) = . В частности если f(x)≡1, то все коэффициенты Фурье, кроме первого, обращаются в нуль  (***)

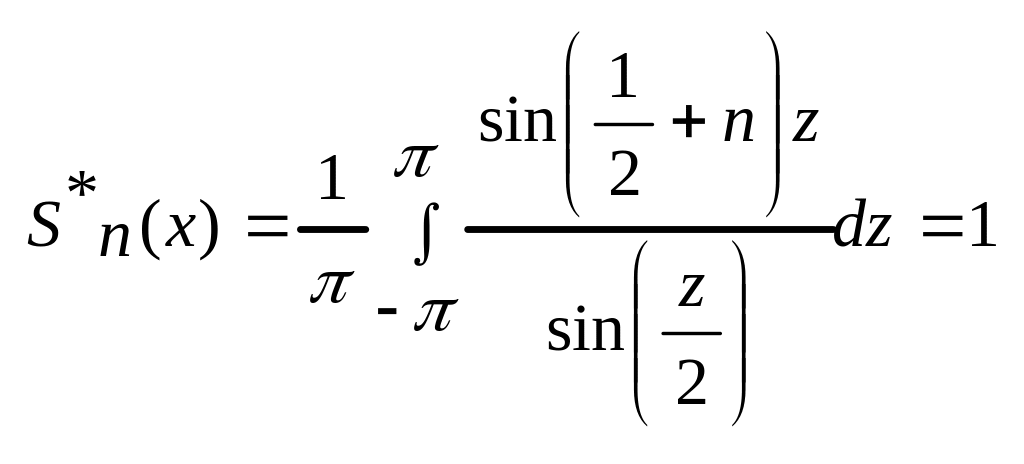Трм.1.:(о сходимости ряда Фурье к функции f(X)).

Если периодическая с периодом 2π функция f(x) и её производная f '(x) кусочно-непрерывны на любом конечном отрезке действительной оси, то ряд Фурье (1) для этой функции сх-ся в каждой точке к среднему арифметическому односторонних пределов функции f(x) в точке x. Т.е. для .

Док-во: Воспользуемся тождеством (***) и составим сумму: . Тогда для док-ва достаточно показать, что разность (3) имеет предел 0 при n∞, т.е. . Представим R_n(x) в интегральной форме.

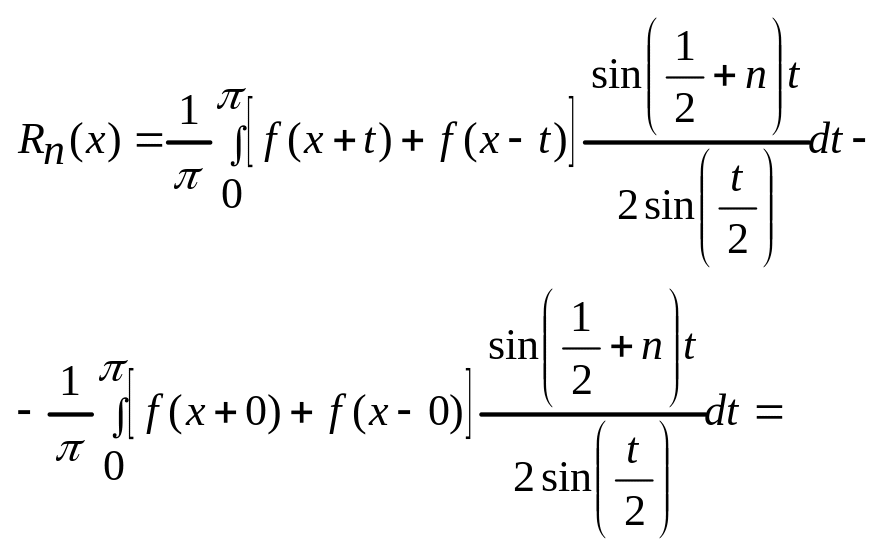(4) . Рассмотрим первый интеграл I₁ в (4) и заметим, что 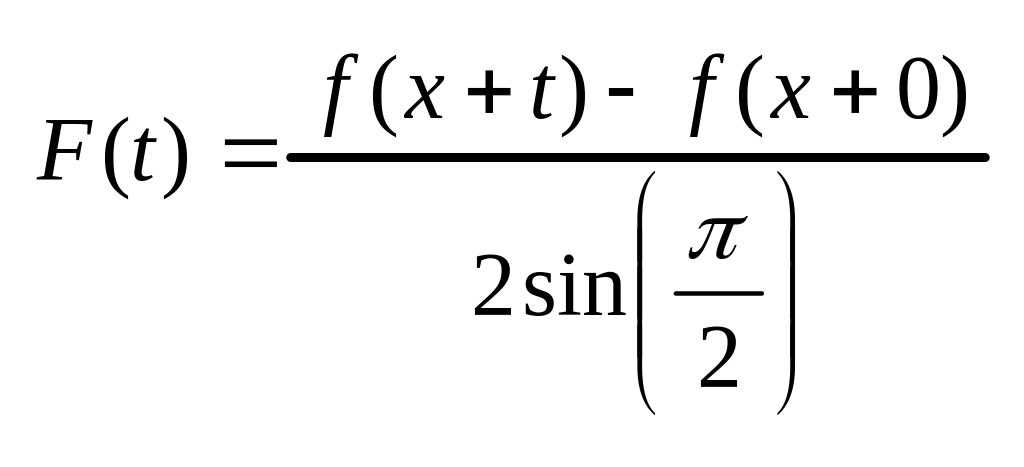, рассматриваемая на [0,π] в точке t=0, имеет устранимый разрыв, т.к. 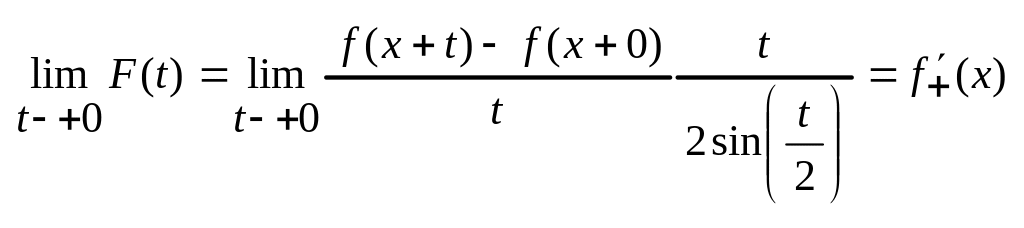. Тогда отсюда и из условия теоремы вытекает, что функция F(t) имеет либо устранимый разрыв, либо разрыв конечного скачка  она кусочно-непрерывна на [0,π]  (по св-ву конечно-непрерывных функций)  в любой точке x, ч.т.д.

Следствие: Если при соблюдении всех условий трм.1 функция ещё и непрерывна, то р. Фурье для неё сходится к значению этой функции в любой точке x.

8. Разложение кусочно-непрерывных на отрезке [а,b] функций в тригонометрические ряды Фурье. Теорема о равномерной сходимости тригонометрического ряда Фурье.

Разложение кусочно-непрерывных на отрезке [а,b] функций в тригонометрические ряды Фурье.

Рассмотрим кусочно-непрерывные функции с основным периодом 2π и рассмотрим их ОнСФ (ортонормированную сис-му ф-ий): 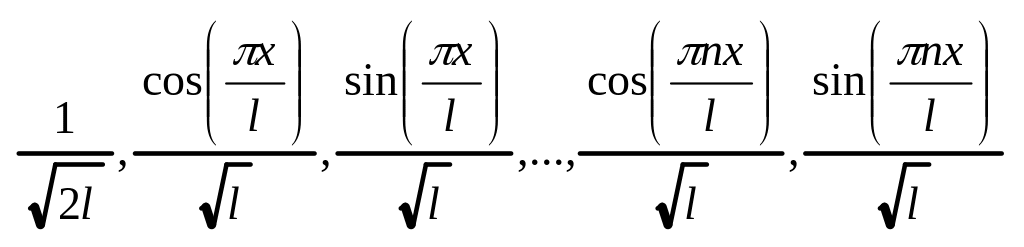. Тогда согласно определению тригонометрического ряда Фурье, для непрерывной на [-l,l] функции f(x) получаем: , где , , . Теорема о сх-ти ряда Фурье к функции f(x) остаётся справедливой и для периодической функции f(x) с периодом 2l. Рассмотрим случай чётных и нечётных периодических функций с периодом T=2π:

1) f(x) - чётная 

2) f(x) - нечётная  .

Трм.1.:(О равномерной сходимости ряда Фурье).

Если периодическая на всей действительной оси с основным периодом T=2π функция f(x) непрерывна и имеет кусочно-непрерывную производную на всей действительной оси, тогда ряд Фурье для f(x) сх-ся равномерно на всей действительной оси к этой функции f(x).

Док-во: Пусть a₁< a₂< a₃<…< a_k – точки разрыва производной f '(x) на [-π, π]. Тогда, интегрируя по частям и принимая во внимание, что f(π)=-f(-π) получаем: . Значит, сделав также для b_n, получим: , где - коэффициенты Фурье для кусочно-непрерывной f '(x). Тогда общий член ряда Фурье: . Но из теоремы о свойстве коэффициентов ряда Фурье следует, что ряд сх-ся. Но тогда, применяя признак Вейерштрассе к нашему ряду  наш ряд будет сходиться равномерно при всех x[-∞,∞] (где определена f(x)) и имеет место равенство .