13.Теорема о повторном интегрировании для кратного интеграла.
Пусть
J={(x1,…,xk)|ai≤xi≤bi
(i=1,…k)}
промежуток в Rk
и пусть J*={(x1,…,xm)|aj≤xj≤bj(j=1,…k)
1≤m≤k}
и пусть J*
- проекция J
на пространство
,а
J**={(xь,xm+1…,xm)|aj≤xj≤bj(j=m+1,…k)}
проекция J
на
,
f(x):(JcRk)→R
интегрируема по Риману на J
и пусть существует
(x1,x2,…,xm)cJ*,
тогда
Док-во совершенно аналогично случаю для R2 , если x1~u=u(x1,x2,…,xm), x2~u=u(xm+1,xm+2,…,xk)
14. Замена переменных в кратном интеграле. Полярные и сферические координаты.
Пусть функция
,
,
dx=dx1dx2…dxk,
dy=dy1dy2…dyk
-
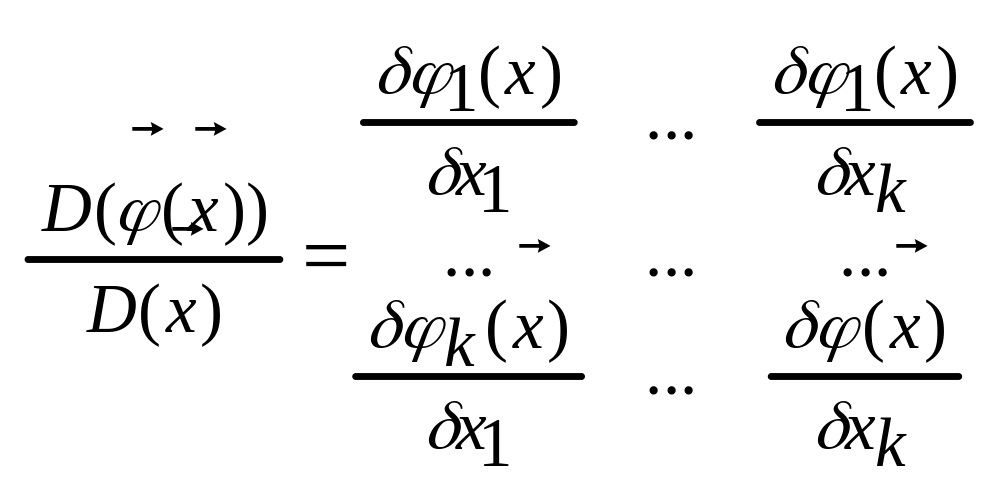якобиан преобразования
,
отличный от нуля почти всюду в E.
Пусть
интегрируема по Риману на этом мн-ве
E*=φ(E),
тогда
.
Теорема
принимается без доказательства.
Сформулируем теорему для к=2 и к=3
R2:
; x=φ(uv),y=ψ(uv),
D→D*
φ,ψcC1(E)
R3:
x=φ(uvw)
y=ψ(uvw) V→V* φψχ c C1V*
z=χ(uvw)
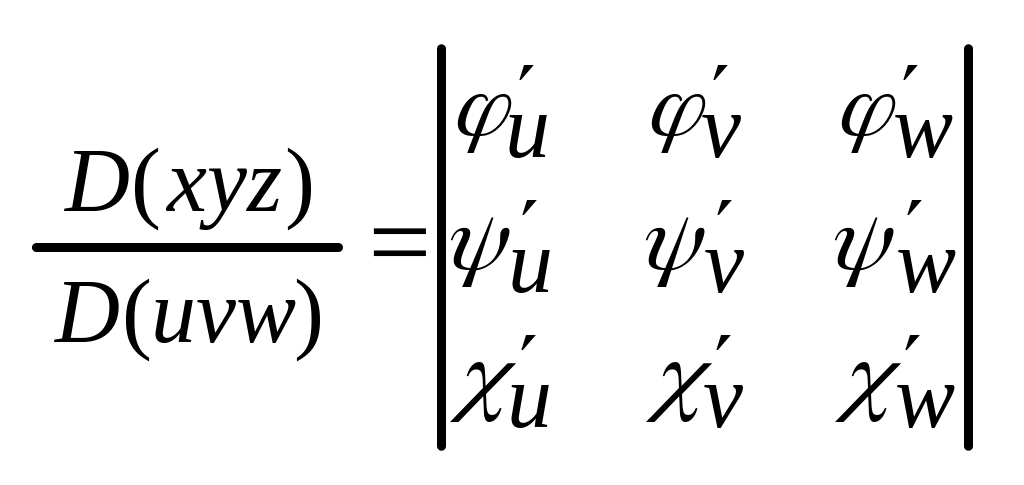
Полярные координаты в двойном интеграле.
x=r∙cosφ
y=r∙sinφ
Сферические координаты в тройном интеграле
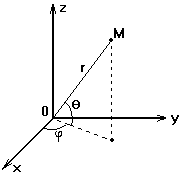
x=r∙cosθ∙cosφ 0≤φ≤2π
y=r∙cosθ∙sinφ -π/2≤θ≤π/2
z=r∙sinθ