Формирование бинарного дерева.

При формировании бинарного дерева нужно задать некоторые ограничения. Рассмотрим пример, когда необходимо построить дерево из n вершин, имеющее минимальную высоту. Для достижения минимальной высоты необходимо, чтобы все уровни дерева, кроме, может быть, последнего, были заполнены. Для того чтобы сделать такое распределение, все поступающие нужно распределять поровну: слева и справа.

n=1 n=2 n=3 n=4 n=5 n=6 n=7

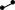
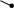
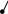
Таким образом, правила для равномерного распределения при известном числе узлов n можно сформулировать с помощью следующего рекурсивного алгоритма:

1. взять один узел в качестве корня;

2. построить левое поддерево с количеством узлов n _l = [n / 2] тем же способом;

3. построить правое поддерево с количеством узлов n _r = n – n _l – 1 тем же способом.

Описание узла дерева на языке Turbo Pascal выглядит таким образом:

Type ElPtr = ^Element

Element = record

Data: integer;

L_Son, R_Son: ElPtr;

end;

Идеально сбалансированное дерево обладает определенным свойством таким, что относительно каждого узла дерева количество узлов в левом и правом поддеревьях может отличаться максимум на 1.

Function Tree (n: integer): ElPtr;

var nl, nr, x: integer;

NewElement: ElPtr;

begin

if n=0 then Tree:=nil

else begin

nl:=n div 2;

nr:=n – nl – 1;

read (x); New (NewElement);

with NewElement do begin

Data:=x;

L_Son:=Tree (nl);

R_Son:=Tree )nr);

end;

Tree:=NewElement;

end;

end;

Эффективность рекурсивного определения заключается в том, что оно позволяет с помощью конечного высказывания определить бесконечное множество объектов.

Применение бинарных деревьев в алгоритмах поиска.

В односвязном списке невозможно использовать бинарные методы, они могут использоваться только в последовательной памяти. Однако, если использовать бинарные деревья, то в такой связной структуре можно получить алгоритм поиска со сложностью O(log ₂ N). Такое дерево реализуется следующим образом: для любого узла дерева с ключом T_i все ключи в левом поддереве должны быть меньше T_i, а в правом – больше T_i. В дереве поиска можно найти место каждого ключа, двигаясь, начиная от корня и переходя на левое или правое поддерево, в зависимости от значения его ключа. Из n элементов можно организовать бинарное дерево (идеально сбалансированное) с высотой не более чем log ₂ N, которое определяет количество операций сравнения при поиске.

Function Search (x: integer; t: ElPtr): ElPtr;

{

T_i

L_Son R_Son

поле Data заменим на поле Key}

v ar f: boolean;

b egin

f

< T_i > T_i

:=false;

while (t<>nil) and not f do

if x=t^. key then f:=true

else if x>t^. key then t:=t^. R_Son else t:=t^. L_Son;

Search:=t;

end;

Если получим, что значение функции = nil, то ключа со значением x в дереве не найдено.

Функцию можно упростить, если организовать идею барьера, когда все листья указывают на введенный фиктивный элемент.

S

F unction Search (x: integer; t: ElPtr): ElPtr;

begin

S^.key:=x;

while t^.key<>x do

if x > t^.key then then t:=t^. R_Son else t:=t^. L_Son;

Search:=t;

end;