11. Ортонормированный базис конечномерного евклидового пространства.

Ортогональный базис — базис, составленный из попарно ортогональных векторов.

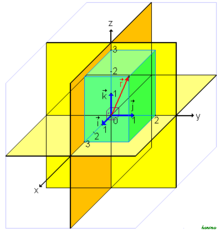
Ортонормированный базис в 3-мерном евклидовом пространстве

Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.

Последнее удобно записывается при помощи символа Кронекера:

то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( ), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.

Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.

Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).

Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.

Коэффициенты в разложении вектора по ортогональному базису:

можно найти так:

.

Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:

12. Неравенство Коши - Буняковского.

Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.

Пусть дано линейное пространство со скалярным произведением . Пусть  — норма, порождённая скалярным произведением, то есть . Тогда для любых имеем:

причём равенство достигается тогда и только тогда, когда векторы и пропорциональны (коллинеарны).

Комментарии

В конечномерном случае можно заметить, что , где  — площадь параллелограмма, натянутого на векторы и .

В общем случае:

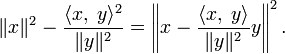
13. Понятие нормы

Норма алгебраического числа — теоретико-числовая функция, норма, определённая в конечном алгебраическом расширении поля. Норма алгебраического числа равна произведению всех корней минимального многочлена данного числа. Норма отображает кольцо целых элементов расширения поля в кольцо целых элементов поля. Часто в качестве поля берется поле рациональных чисел , а значит в качестве кольца его целых элементов берется кольцо целых чисел .

Норма в кольце гауссовых целых чисел

Поле - расширение поля рациональных чисел, кольцо его целых элементов - это кольцо гауссовых целых чисел чисел вида . Норма определяется как . Для данной нормы - простое число в тогда и только тогда, когда - простой элемент кольца . Таким образом, в 2 и все простые числа вида разложимы в , а простые вида - неразложимы, поэтому .

Множество обратимых элементов кольца состоит из 4-х элементов: , норма только этих элементов равна 1.