0. Решение уравнений первой степени с одной переменной

Рассмотрим линейное уравнение где и – некоторые числа.

Решим уравнение при помощи равносильных преобразований. При , . Таким образом, если , то (уравнение имеет единственный корень).

В случае уравнение имеет вид .

Если , то уравнение не имеет корней, а если , то любое (действительное) число является корнем уравнения.

Ответ: 1) при имеет единственный корень ,

2) при и не имеет корней,

3) при и имеет бесконечно много корней.

Любое уравнений первой степени с одной переменной можно преобразовать в равносильное линейное уравнение (свойство 1).

Например, при решении уравнения упрощают выражение, стоящее в левой части. К полученному уравнению применяются свойства равносильных уравнений (п. 2.2.3):

0. Решение уравнений с одной переменной степени выше первой

В 7-м классе учащиеся решают целые уравнения степени выше первой, используя свойства равенства произведения нулю: и т.п. К уравнению такого вида обычно приводится с помощью равносильного преобразования и разложения на множители уравнение .

В случае целого уравнения, если разлагается на множители, то имеем:

Квадратные уравнения имеют важное прикладное значение, к ним сводятся многие трансцендентные уравнения (показательные, логарифмические, тригонометрические).

«Квадратным уравнением называется уравнение вида , где – переменная, , и – некоторые числа, причём » [3, с. 286].

Решается полное квадратное уравнение с помощью метода разложения на множители его левой части и при помощи равносильных преобразований.

Решим квадратное уравнение. Так как , то

Числитель дроби , т.е. выражение , называют дискриминантом квадратного уравнения . Его обозначают буквой D. Значит, . Используя обозначение дискриминанта, последнее уравнение можно записать в виде .

Знаменатель дроби положителен, так как по определению квадратного уравнения . От D зависит, какие значения (положительные, нуль или отрицательные) принимает эта дробь. Рассмотрим отдельно каждый случай.

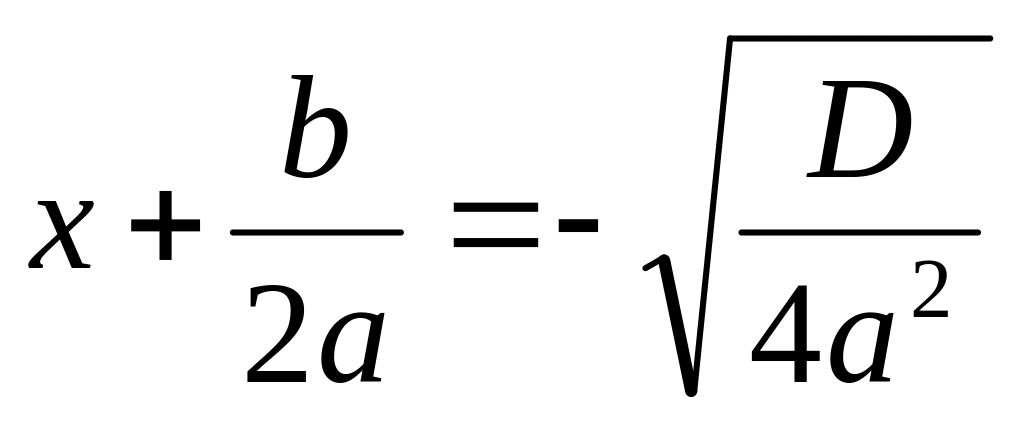1. Если , то . Получаем или , т.е.

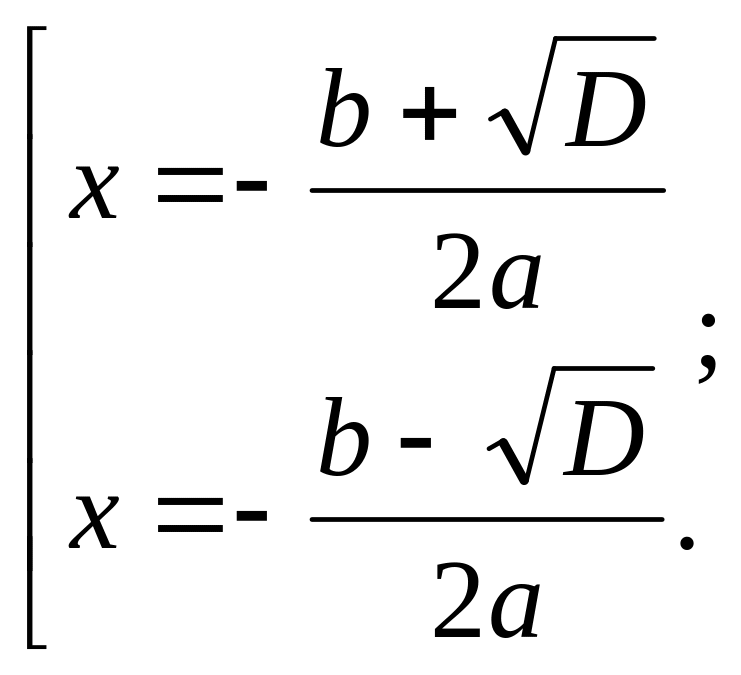
Уравнение в этом случае имеет два корня: и .

2. Если , то .

Уравнение в этом случае имеет один корень .

3. Если , то . В этом случае уравнение не имеет действительных корней.

В 8-м классе с изучением алгебраических дробей решаются дробно-рациональные уравнения с одной переменной: . Используя условие равенства дроби нулю, получим:

Таким образом, при решении уравнений используются свойства равносильных уравнений. Кроме основных свойств равносильных уравнений для каждого вида уравнений изучаются другие приемы. Так, целые уравнения чаще всего решаются с помощью метода разложения на множители, в более сложных из них используется метод введения новой переменной (метод подстановки).

Введение новой переменной как прием равносильных преобразований уравнений

Суть этого метода по отношению к уравнению состоит в том, чтобы найти функции и , для которых при любом (т.е. для любого значения из области определения уравнения) выполняется равенство

В этом случае достаточно решить уравнение , а затем для каждого его корня решить уравнение (*). Совокупность всех полученных таким образом корней х уравнения (*), таких что , будет искомым множеством решений исходного уравнения. Функция называется подстановкой.

В случае алгебраических уравнений, как правило, в роли применяются многочлены, дроби или радикалы. В учебнике для 9-го класса [5] метод решения уравнений степени выше двух носит название метода введения новой переменной.

Задание № 7 для самостоятельной работы.

1. Проведите логико-математический анализ изучения алгебраических неравенств [4], [5], [33]. Сделайте выводы.

2. Проведите логико-математический анализ изучения трансцендентных неравенств [6], [34]. Сделайте выводы.