• Количественная оценка эффективности решений: функция полезности

Показатели исхода операции (ПИО) и их связь с показателями эффективности для трех категорий операций (детерминированных, стохастических, с неопределенностью). Полезность исходов операции, ранжирование исходов. Функция полезности: определение и свойства, виды и примеры.

22. Технология программирования Тоичкин н.А.

• Рекурсивные алгоритмы. Примеры рекурсивных алгоритмов

Определение рекурсии. Рекурсия. Рекуррентное соотношение. Рекурсивный алгоритм. Глубина рекурсии. Конечность и окончание рекурсивного алгоритма. Схемы прямой (простой) и косвенной (сложной) рекурсии. Реализация механизма рекурсивного вызова процедуры. Рекурсивные данные. Примеры рекурсивных алгоритмов. Рекурсия и итерация.

• Анализ временной сложности (трудоемкости) алгоритмов

Цель анализа временной сложности (трудоемкости) алгоритмов. Факторы, влияющие на сложность алгоритмов. что подсчитывать и что учитывать при анализе сложности. наилучший, наихудший и средний случай работы алгоритма. асимптотическая сложность. Примеры анализа сложности алгоритмов внутренняя сортировка массивов (сортировка вставками, сортировка обменом). бинарный поиск (поиск в отсортированном массиве); поиск подстроки в строке (примитивный алгоритм, алгоритм КМП).

23. Численные методы/Вычислительная математика Малыгина с.Н.

• Постановка задач аппроксимации функций одной переменной: Интерполирование алгебраическими многочленами.

В основе большинства численных методов математического анализа лежит подмена одной функции 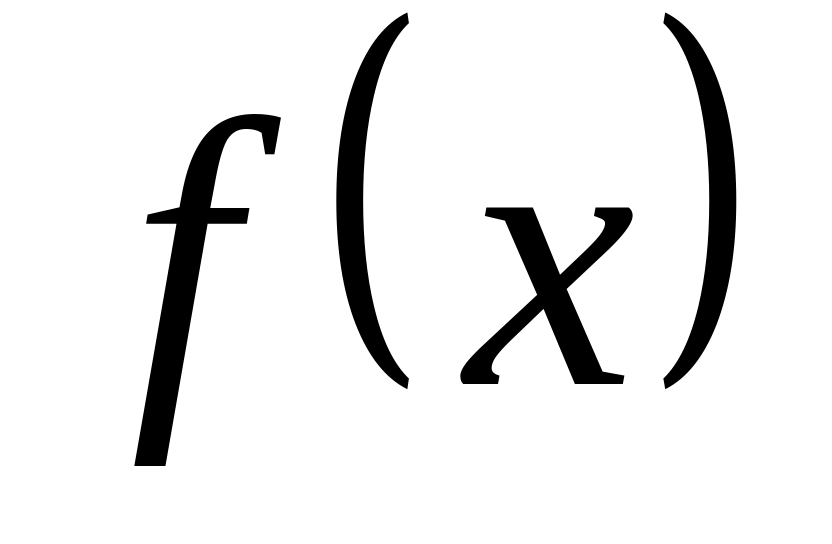(известной, неизвестной или частично известной) другой функцией 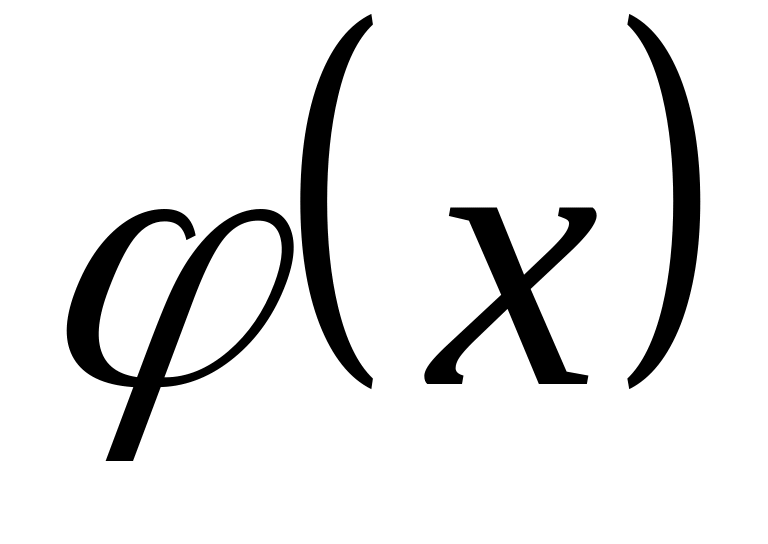, близкой к и обладающей «хорошими» свойствами, позволяющими легко производить над нею те или иные аналитические или вычислительные операции. Такая подмена называется аппроксимацией или просто приближением функции функцией . Такую подмену можно сделать разными способами. Интерполирование Постановка задачи, пример возникновения задачи интерполирования Интерполирование алгебраическими многочленами Пусть на отрезке 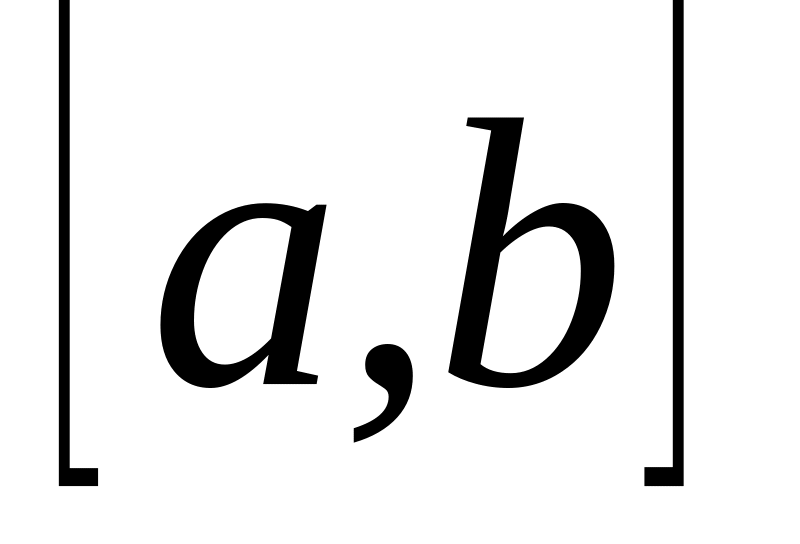заданы точки (будем называть их узлами интерполирования), в которых известны значения функции . 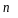Задача интерполирования алгебраическими многочленами состоит в том, чтобы построить многочлен степени 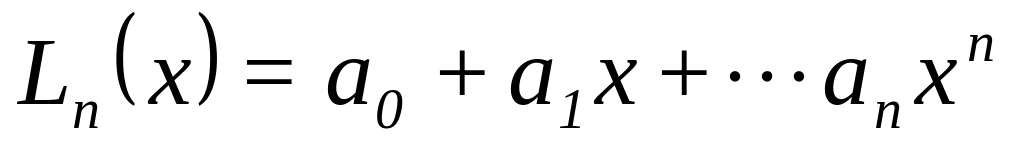, (1) значения которого в заданных точках совпадают со значениями функции в этих точках. Для любой непрерывной функции сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов получаем систему линейных уравнений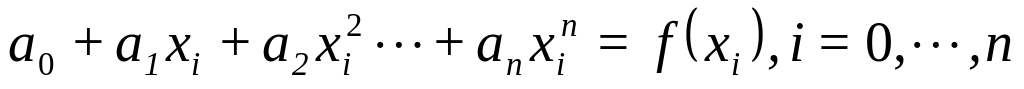 (2) Если среди нет совпадающих, то определитель системы (1.2) отличен от нуля, и следовательно система имеет единственное решение. Определение Многочлен , удовлетворяющий условию (3) называется интерполяционным многочленом для функции , построенным по узлам . Решение системы (1.2) можно записать различным образом. Наиболее употребительна запись интерполяционного многочлена в форме Лагранжа и в форме Ньютона. Интерполяционный многочлен Лагранжа имеет вид (4) Интерполяционная формула Ньютона позволяет выразить интерполяционный многочлен через значения в одном из узлов и через разделенные разности функции , построенные по узлам . Интерполяционным многочленом Ньютона называется многочлен , (5) где 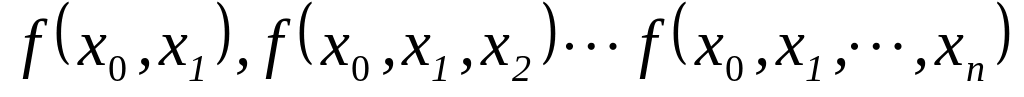- разделенные разности. Интерполяционную формулу Ньютона удобнее применять в том случае, когда интерполируется одна и та же функция , но число узлов интерполирования увеличивается. Если узлы интерполяции фиксированы и интерполируется не одна, а несколько функций, то удобнее пользоваться формулой Лагранжа.