.Решение задачи линейного программирования симплекс-методом.

Прямая задача.

Рассмотрим задачу линейного программирования в канонической форме:

Найти максимум (минимум) функции 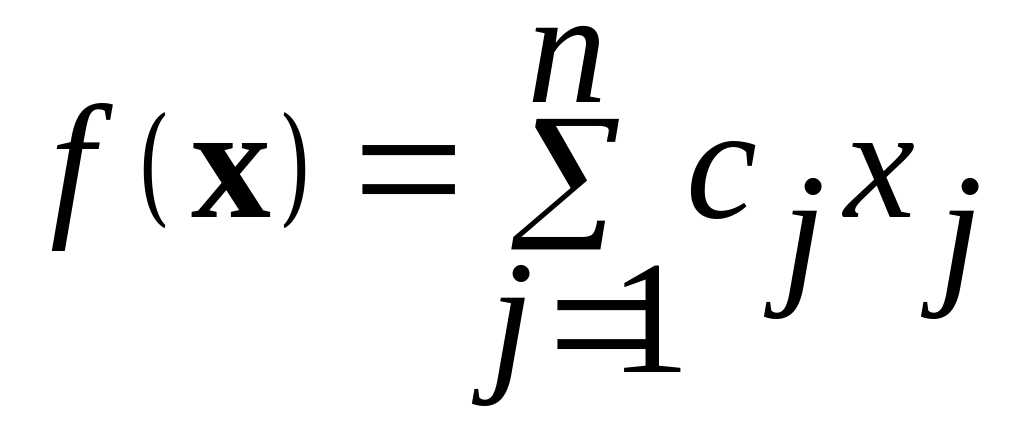при условиях

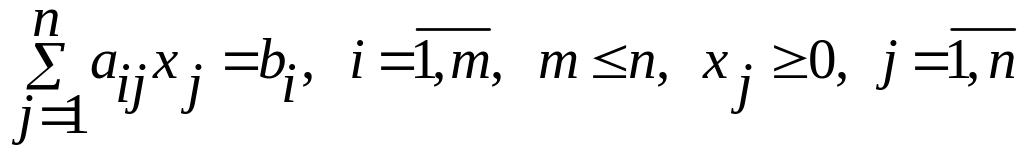
Предполагается, что решение этой задачи существует. Чтобы найти оптимальное решение, надо найти допустимые базисные решения, а из них выбрать оптимальное базисное решение.

Симплекс – метод – это алгебраический метод решения задач линейного программирования. В процессе вычислений производиться последовательный обход вершин многогранника решений (ОДР.) с проверкой в каждой вершине условий оптимальности. При этом каждый переход в смежную вершину сопровождается улучшением целевой функции.

Вычислительные процедуры симплекс - метода.

При графическом методе решения ЗЛП оптимальному решению соответствует всегда одна из угловых (экстремальных) точек пространства решений. Это результат положен в основу построения симплекс-метода. Симплекс-метод не обладает наглядностью геометрического представления пространства решений. Симплекс-метод реализует упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки, осуществляются последовательные переходы от одной допустимой экстремальной точки к другой, пока не будет найдена точка оптимального решения.

Обозначим: – общее количество переменных в ЗЛП, представленной в канонической форме; - количество исходных переменных; - количество ограничений, - количество дополнительных переменных, тогда .

Каждая вершина многогранника решений имеет - ненулевых переменных и ( ) - нулевых переменных.

Ненулевые переменные называются базисными, нулевые переменные – небазисными.

Дополним систему равенств равенством целевой функции, при этом будем считать, что является базисной переменной, которая всегда присутствует в базисе для любой вершины.

Для получения решения составляется начальный допустимый базис, в котором базисные переменные должны быть представлены в виде единичных орт. Это означает, что уравнения, представляющие данную вершину должны включать каждую базисную переменную только в одной строке с коэффициентом, равным 1.

При выборе начального допустимого базиса для составления симплекс-таблицы на первом шаге СТ(0) исходные переменные приравниваются к нулю и являются небазисными, среди введённых дополнительных переменных выбираются переменные с коэффициентами равными единице. Переменные в равенствах (7) - (9) являются базисными и в - строку входят с коэффициентами, равными 0. Для заполнения симплекс-таблицы необходимо целевую функцию преобразовать к виду 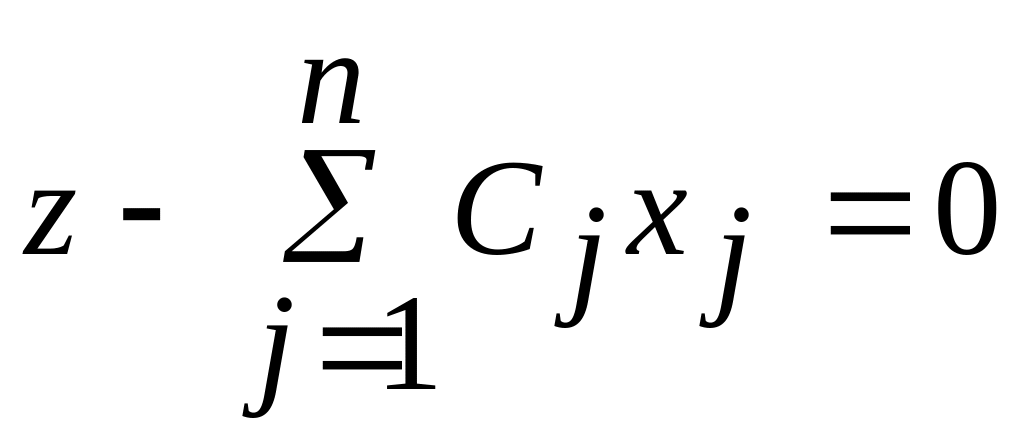. Таким образом, окончательно получаем:

(6)

(7)

(8)

(9)

При составлении симплекс-таблицы придерживаются следующих правил:

в крайнем левом столбце располагаются базисные переменные и ;

в крайнем правом столбце располагаются правые части ограничений;

в первой строке располагаются переменные в определённом порядке:

сначала , потом небазисные переменные, базисные переменные располагаются в последних столбцах перед правой частью (ПЧ). Запишем коэффициенты в СТ(0):

							Свободные члены
	1	-	-	0	0	0	0
	0			1	0	0
	0			0	1	0
	0			0	0	1

Оптимальность любой из вершин определяется коэффициентами при небазисных переменных в – строке текущей симплекс-таблицы:

Для задачи максимизации данная вершина является оптимальной, если все коэффициенты при небазисных переменных в – строке являются неотрицательными (>0);

Для задачи минимизации данная вершина является оптимальной, если все коэффициенты при небазисных переменных в – строке являются неположительными (< 0).

Если в задаче максимизации (минимизации) у одной небазисной переменной в – строке коэффициент <0(>0), то текущая точка не является оптимальной и необходимо изменить базис. Для этого выбирают небазисную переменную, имеющую максимально отрицательный (положительный) коэффициент в – строке. Выбранная небазисная переменная будет включаться в новый базис, поэтому называется включаемой переменной. Базисная переменная, которая будет выведена из базиса, называется исключаемой переменной.

Исключаемой переменой будет та базисная переменная, которая первой обратится в "0" при переходе в смежную вершину после ввода включаемой переменной.

Столбец исключаемой переменной будем называть разрешающим столбцом.

Строку исключаемой переменной будем называть разрешающей строкой.

Пересечение разрешающего столбца и строки определяют разрешающий элемент (РЭ).

Чтобы определить исключаемую переменную необходимо:

разделить правые части всех базисных переменных (кроме - строки) на соответствующие положительные коэффициенты разрешающего столбца;

выбрать из полученных отношений наименьшее.

Делить на "0" и отрицательную величину нельзя, т. к. это приводит к отсутствию пересекающейся вершины или к вершине вне ОДР.

Для перехода в смежную вершину необходимо сформировать матрицу перехода B(0), которая определит связь между СТ(0) и СТ(1): СТ(1) = В(0) СТ(0).

Для произвольной квадратной матрице размерности n, имеющей в качестве (n - 1) столбца единичные орты, расположенные в соответствии с единичными ортами единичной матрицы, и одного произвольного столбца с ненулевым элементом на главной диагонали, обратная матрица находится по следующему правилу:

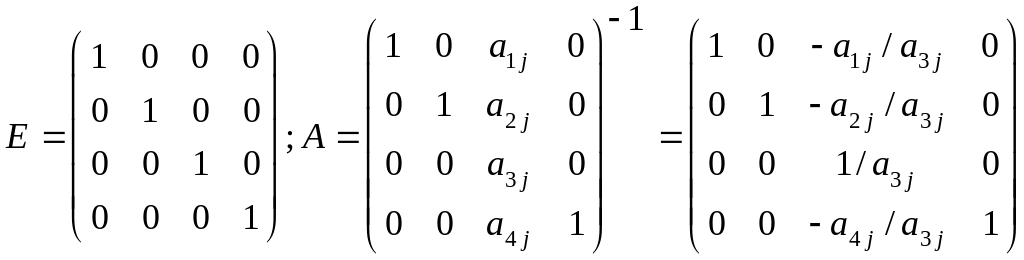
Каждый элемент j – столбца делится на РЭ и меняет знак на противоположный, кроме разрешающего элемента.

Возможен другой вариант размещения симплекс-таблиц. Сведем систему ограничений к единичному базису: 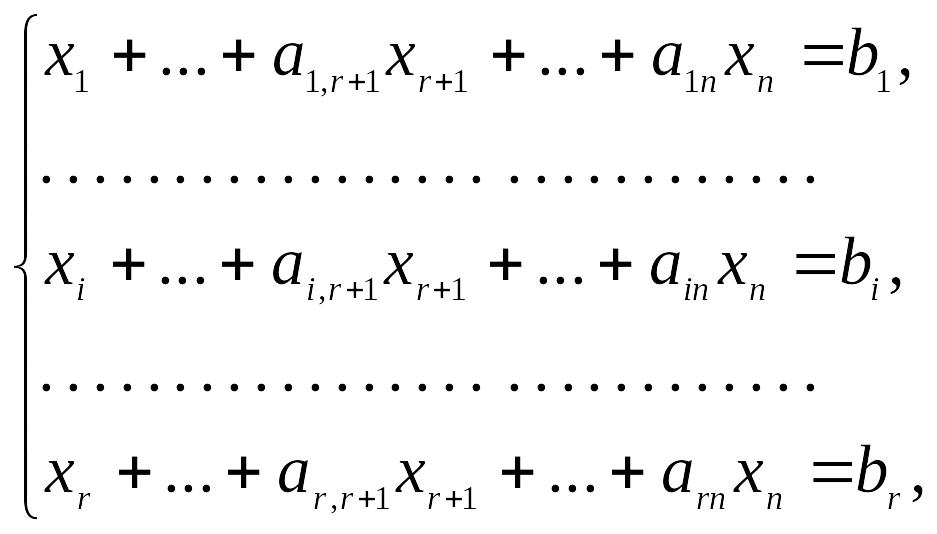а линейную форму L - к виду L+ γ_r+1 x_r+1+…+ γ_j x_j +…+ γ_n x_n=γ₀. (10)

В виде таблицы эти данные можно представить так:

Базисные переменные	Свободные члены	x1	…	xi	…	xr	xr+1	…	xj	…	xn
x1	b1	1	…	0	…	0	a1,r+1	…	A1j	…	a1n
…	…	…	…	…	…	…	…	…	…	…	…
xi	bi	0	…	1	…	0	ai,r+1	…	aij	…	ain
…	…	…	…	…	…	…	…	…	…	…	…
xr	br	0	…	0	…	1	ar,r+1	…	arj	…	arn
L	γ0	0	…	0	…	0	γr+1	…	γj	…	γn

Равенство (10) будем называть приведенным (к свободным переменным) выражением для функции L, а коэффициенты γ_j - оценками (индексами) соответствующих свободных переменных x_j.

1. Выбираем разрешающий столбец a_p из условия: оценка γ_p<0 и хотя бы один элемент a_ip>0.

2. Выбираем q-ю разрешающую строку из условия b_q/a_qp=min{b_i / a_ip} для a_ip>0.

3. Производим пересчет элементов разрешающей q-й строки по формуле a'_qk= a_qk/a_qp (k=0,1,…,n).

4. Вычисляем элементы всех остальных строк (при k≠p) по формуле a'_ik= a_ik - a'_qk∙a_ip (i=0,1,…,q-1,q+1,…,r) .

Следует иметь в виду следующую теорему.

Теорема. Если после выполнения очередной итерации:

1. найдется хотя бы одна отрицательная оценка и в каждом столбце с такой оценкой окажется хотя бы один положительный элемент, т.е. γ_k<0 для некоторых k, и a_ik>0 для тех же k и некоторого i, то можно улучшить решение, выполнив следующую итерацию;

2. найдется хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, т.е. γ_k<0, a_ik<0 для какого-то k и всех i, то функция L не ограничена в области допустимых решений (L_max→ ∞);

3. все оценки окажутся неотрицательными, т.е. γ_k≥0 для всех k, то достигнуто оптимальное решение.

Рассмотрим реализацию симплекс-метода на конкретном примере. Найдем наибольшее значение линейной функции L=7x₁+5x₂ на множестве неотрицательных решений системы уравнений

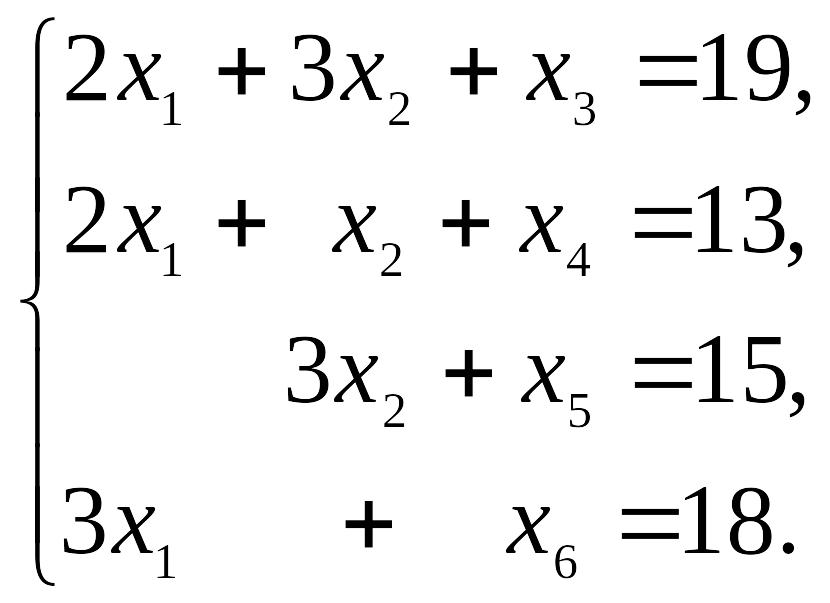
Решение. Ранг матрицы системы уравнений 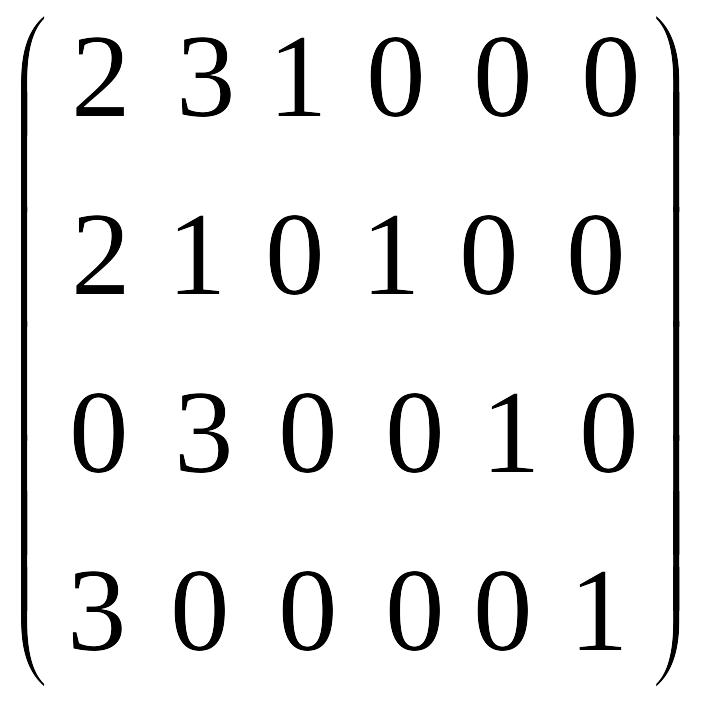равен 4. Ранг расширенной матрицы также равен 4. Следовательно, четыре переменные (базисные) можно выразить через две (свободные), т.е.

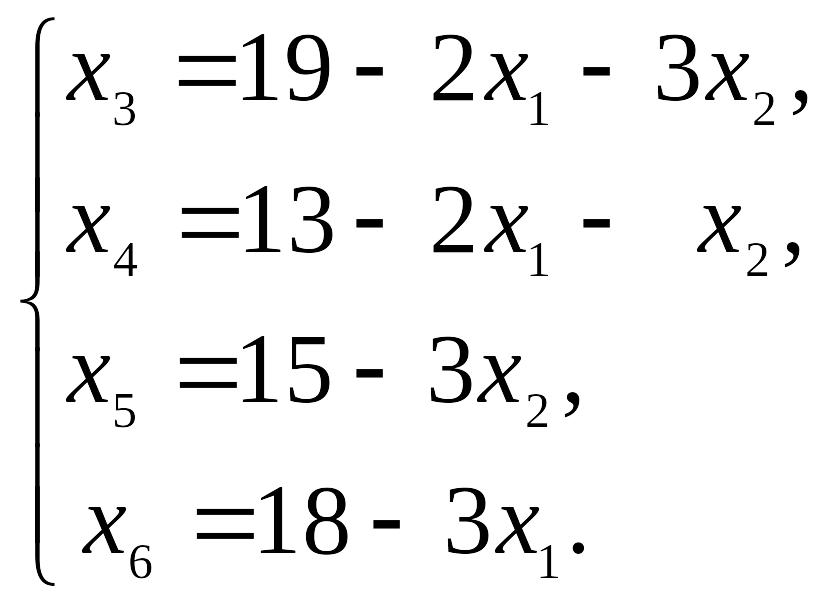
Линейная форма L=7x₁+5x₂ уже выражена через свободные переменные. В этом равенстве перенесем в левую часть все члены, содержащие переменные: L-7x₁-5x₂=0.

Теперь можно составить исходную симплекс-таблицу:

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5	x6
x3	19	2	3	1	0	0	0	19/3
х4	13	2	1	0	1	0	0	13/1
x5	15	0	3	0	0	1	0	15/3
x6	18	3	0	0	0	0	1
L	0	-7	-5	0	0	0	0

Выясним, имеются ли в последней строке (индексной) отрицательные оценки. Таких оценок две: -7 и -5. Берем, например, ‑5 и просматриваем столбец x₂. В этом столбце имеется три положительных элемента: 3, 1, 3. Делим на эти числа соответствующие свободные члены: 19/3, 13/1, 15/3. Из полученных частных выбираем наименьшее - 15/3. Следовательно, разрешающим является элемент 3, стоящий на пересечении столбца x₂ и строки x₅. Тогда в новый базис вместо переменной x₅ войдет переменная x₂. Для перехода к следующей симплекс-таблице умножаем строку x₅ исходной таблицы на 1/3, чтобы получить на месте разрешающего элемента 1. Полученную таким образом строку пишем в новой симплекс-таблице на месте прежней строки (теперь уже под именем x₂). К каждой из остальных строк прибавляем вновь полученную, умноженную на такое число, чтобы в клетках столбца x₂ появились нули. Записываем преобразованные строки в новой симплекс-таблице. Этим завершается первая итерация.

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5	x6
x3	4	2	0	1	0	-1	0	4/2
x4	8	2	0	0	1	-1/3	0	8/2
x2	5	0	1	0	0	1/3	0
x6	18	3	0	0	0	0	1	18/3
L	25	-7	0	0	0	5/3	0

Теперь все рассуждения повторяем применительно к полученной таблице, т.е. выполняем вторую итерацию. Новый разрешающий элемент, находящийся на пересечении строки x₃ и столбца x₁, есть 2. Переходим к следующей таблице.

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5	x6
x1	2	1	0	1/2	0	-1/2	0
x4	4	0	0	-1	1	2/3	0	4/(2/3)
x2	5	0	1	0	0	1/3	0	5/(1/3)
x6	12	0	0	-3/2	0	3/2	1	12/(3/2)
L	39	0	0	7/2	0	-11/6	0

Проводим преобразования полученной таблицы. Здесь разрешающим является элемент 2/3, находящийся на пересечении столбца x₅ и строки x₄. Получим:

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5	x6
x1	5	1	0	-1/4	3/4	0	0
x5	6	0	0	-3/2	3/2	1	0
x2	3	0	1	1/2	-1/2	0	0
x6	3	0	0	3/4	-9/4	0	1
L	50	0	0	3/4	11/4	0	0

Поскольку в индексной строке нет отрицательных оценок, мы получили оптимальный план (5,3,0,0,6,3). Он находится в столбце свободных членов. Соответствующее этому плану значение целевой функции равно 50. Итак, L_max=L(5,3,0,0,6,3)=50.

Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений " ≤ ").

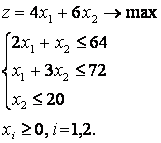
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:

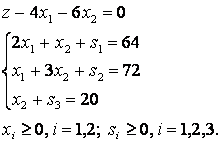
Эта система является системой с базисом (базис s₁, s₂, s₃, каждая из них входит только в одно уравнение системы с коэффициентом 1, x₁ и x₂ - свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами:

• система ограничений должна быть системой уравнений с базисом;

• свободные члены всех уравнений в системе должны быть неотрицательны.

Полученная система - система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0) для решения задачи на симплекс-метод, т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь "БП" означает столбец базисных переменных, «свободные члены» - столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.

симплекс-метод итерация 0

БП	x1	x2	s1	s2	s3	свободные члены	Отношение
z	-4	-6	0	0	0	0	-
s1	2	1	1	0	0	64	64/1=64
s2	1	3	0	1	0	72	72/3=24
s3	0	1	0	0	1	20	20/1=20

Для улучшения решения перейдем к следующей итерации симплекс-метода, получим следующую симплекс-таблицу. Для этого надо выбрать разрешающий столбец, т.е. переменную, которая войдет в базис на следующей итерации симплекс-метода. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z-строке (в задаче на максимум) – в начальной итерации симплекс-метода это столбец x2 (коэффициент -6).

Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца "свободные члены" к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s3 (коэффициент 20).

Разрешающий элемент находится на пересечении разрешающего столбца и разрешающей строки, его ячейка выделена цветом, он равен 1. Следовательно, на следующей итерации симплекс-метода переменная x2 заменит в базисе s3. Заметим, что в z-строке отношение не ищется, там ставится прочерк " - ". В случае если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то решение задачи бесконечно.

Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований - превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).

1)Вычисление строки х2 таблицы "Итерация 1". Сначала делим все члены разрешающей строки s3 таблицы "Итерация 0" на разрешающий элемент (он равен 1 в данном случае) этой таблицы, получим строку x2 в таблице «Итерации 1». Т.к. разрешающий элемент в данном случае равен 1, то строка s3 таблицы "Итерация 0" будет совпадать со строкой х2 таблицы "Итерация 1". Строку x2 таблицы "Итерации 1" мы получили 0 1 0 0 1 20, остальные строки таблицы "Итерация 1" будут получены из этой строки и строк таблицы "Итерация 0" следующим образом:

2) Вычисление z-строки таблицы "Итерация 1". На месте -6 в первой строке (z-строке) в столбце х2 таблицы "Итерация 0" должен быть 0 в первой строке таблицы "Итерация 1". Для этого все элементы строки х2 таблицы "Итерация 1" 0 1 0 0 1 20 умножим на 6, получим 0 6 0 0 6 120 и сложим эту строку с первой строкой (z - строкой) таблицы "Итерация 0" -4 -6 0 0 0 0, получим -4 0 0 0 6 120. В столбце x2 появился ноль 0, цель достигнута.

3) Вычисление строки s1 таблицы "Итерация 1". На месте 1 в s1 строке таблицы "Итерация 0" должен быть 0 в таблице "Итерация 1". Для этого все элементы строки х2 таблицы "Итерация 1" 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s1 - строкой таблицы "Итерация 0" 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х2 получен необходимый 0.

4) Вычисление строки s2 таблицы "Итерация 1". На месте 3 в s2 строке таблицы "Итерация 0" должен быть 0 в таблице "Итерация 1". Для этого все элементы строки х2 таблицы "Итерация 1" 0 1 0 0 1 20 умножим на -3, получим 0 -3 0 0 -3 -60 и сложим эту строку с s1 - строкой таблицы "Итерация 0" 1 3 0 1 0 72, получим строку 1 0 0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице "Итерация 1" стал единичным, он содержит одну 1 и остальные 0.

Для следующих таблиц пересчет элементов таблицы делается аналогично.

симплекс-метод итерация 1

БП	x1	x2	s1	s2	s3	Свободные члены	Отношение
z	-4	0	0	0	6	120	-
s1	2	0	1	0	-1	44	44/2=22
s2	1	0	0	1	-3	12	12/1=12
x2	0	1	0	0	1	20	-

Разрешающий столбец х1, разрешающая строка s2, s2 выходит из базиса, х1 входит в базис. Совершенно аналогично получим остальные симплекс-таблицы, пока не будет получена таблица со всеми положительными коэффициентами в z-строке. Это признак оптимальной таблицы.

симплекс-метод итерация 2

БП	x1	x2	s1	s2	s3	Свободные члены	Отношение
z	0	0	0	4	-6	168	-
s1	0	0	1	-2	5	20	20/5=4
x1	1	0	0	1	-3	12	-
x2	0	1	0	0	1	20	20/1=20

Разрешающий столбец s3, разрешающая строка s1, s1 выходит из базиса, s3 входит в базис.

симплекс-метод итерация 3

БП	x1	x2	s1	s2	s3	Свободные члены	Отношение
z	0	0	6/5	8/5	0	192	-
s3	0	0	1/5	-2/5	1	4	-
x1	1	0	3/5	-1/5	0	24	-
x2	0	1	-1/5	2/5	0	16	-

В z-строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение x1 = 24, x2 = 16, z_max = 192.