§4. Дифференцируемость и аналитичность фкп

Определение. Пусть задана ФКП . Производной этой функции в точке называется предел

, если этот предел существует и конечен. В этом случае функция называется моногенной или дифференцируемой (в комплексном смысле) в точке .

Определение. Вещественно-значная Функция двух переменных называется дифференцируемой в точке , если в некоторой окрестности этой точки она может быть представлена в виде

,

где и - ,

и б.м. более высокого порядка малости, чем , при .

ТЕОРЕМА (Коши-Римана). Пусть функция определена в некоторой окрестности точки . Для моногенной функции в точке необходимо и достаточно одновременного выполнения двух условий:

1. Функции и 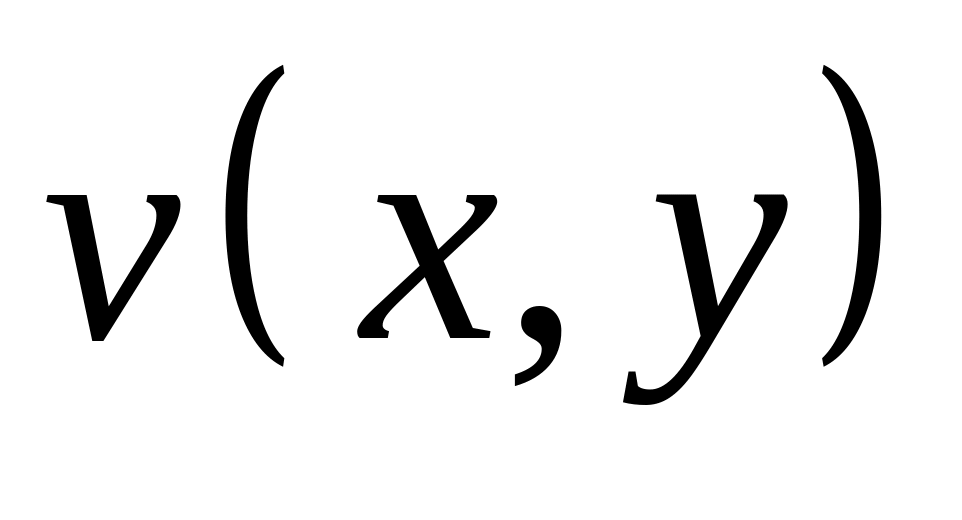дифференцируемы в точке (Как действительно-значные)

2. В точке выполняется условие Коши-Римана (Даламбера-Эйлера):

(без доказательства).

Утверждение 1. Формулы для производной

.

Доказательство. Пусть существует . (Она одинакова по всем направлениям) Вычислим эту производную как предел в точке по направлению, параллельному оси . .

Далее аналогично и/или используя формулу Коши-Римана.

Замечание. Проще вычислять производные не по формуле, а по свойствам аналитических ФКП, которые будут перечислены ниже.

Определение. Функция называется аналитической в точке , если она дифференцируема в некоторой окрестности этой точки.

Функция аналитическая в области , если она аналитична в каждой точке этой области и обозначается , где - пространство аналитических функций в области .

Чтобы найти область аналитичности, надо узнать, в какой области она дифференцируема. (Но это трудоёмко.)

Достаточный признак аналитичности функции в области.

Пусть и непрерывны вместе со своими ЧП 1 порядка в области , а так же удовлетворяют условиям Коши-Римана для всех . Тогда аналитична в .

Пример 1. .

. ( - область, где соблюдается непрерывность ЧП 1 порядка)

, - оба условия выполнены, следовательно аналитична на всей комплексной плоскости, .

ТЕОРЕМА 2. Сумма, разность, произведение и частное (Если знаменатель не обращается в 0) аналитических в точке (области) ФКП также является аналитической ФКП.

ТЕОРЕМА 3. Пусть функция аналитическая в точке , а функция аналитическая в точке . Тогда функция аналитическая в точке .

Замечание. Действительная и мнимая части аналитической функции являются сопряжёнными гармоническими функциями.

Аналитическая функция с точностью до произвольной постоянной однозначно восстанавливается по своей действительной (мнимой) части при помощи условий Коши-Римана.

Глава 2. Интеграл от фкп. Ряды тейлора и лорана.

§1. Интеграл Коши (от фкп)

Определение. Кривая на комплексной плоскости - отображение , где .

Если и - непрерывные кусочно-гладкие функции, то - непрерывная кусочно-гладкая кривая.

Определение. Пусть дано разбиение кривой точками . - длина дуги - максимальная длина участка разбиения дуги.

(1)

- интеграл от ФКП , если этот предел существует и конечен.

Выразим интеграл Коши (1) через криволинейные интегралы от функций действительных переменных.

.

.

(2)

В правой части формулы – криволинейные интегралы 2 рода.

Из формулы (2) из соответствующих свойств криволинейных интегралов вытекают основные свойства интеграла от ФКП:

1. Линейность. (Не нуждается в пояснениях)

2. Аддитивность по путям интегрирования.

3. , где - длина кривой .

4. Равномерный предел последовательности непрерывных функций 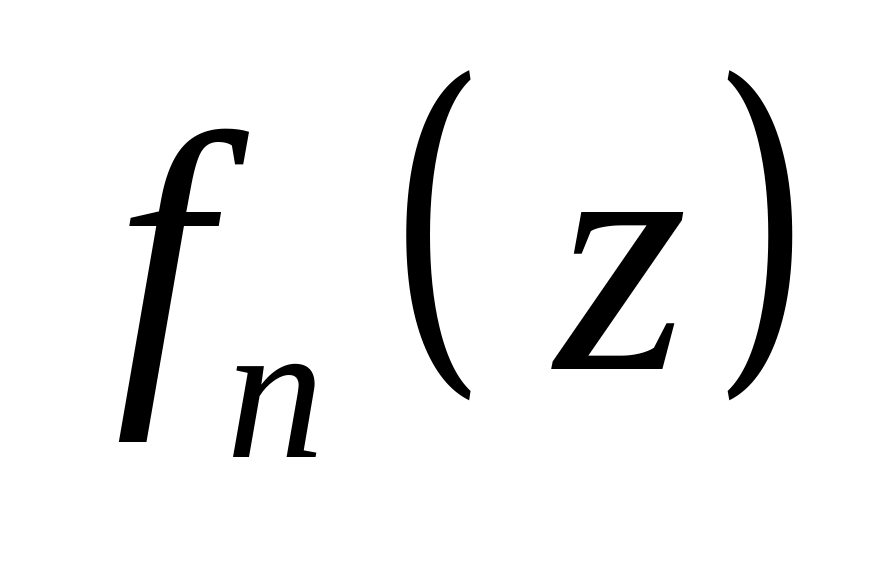интегрируем и .

5. Замена переменной происходит аналогично действительным криволинейным интегралам.