9.3.4. Деякі властивості рядів з довільними дійсними членами

Теорема 4 з п. 9.1 встановлює деякі, так би мовити, "арифметичні" властивості рядів. Вони аналогічні властивостям сум скінченної кількості доданків. Але ряди – це не суми, и їх властивості мають ряд особливостей. Зокрема, це стосується сполучної й переставної властивостей та множення рядів.

Теорема 13. Можна заключати в дужки довільні групи членів збіжного ряду. Сума ряду при цьому не змінюється.

Але, взагалі кажучи, не є припустимим відкидати дужки в збіжних рядах.

Приклад 37. Ряд

збігається до нуля (чому?). але відкидання дужок веде до розбіжного ряду

.

Абсолютно збіжні ряди посідають переставну властивість.

Теорема 14. Можна міняти місцями члени абсолютно збіжного ряду, і при цьому його сума не змінюється.

Умовно збіжні ряди такой властивості не мають, про що свідчить наступна теорема.

Теорема 15 (Ріман¹). Міняючи місцями члени умовно збіжного ряду, ми можемо отримати ряд довільною сумою або навіть розбіжний ряд.

Справедливість теорем 14, 15 заснована на тому, що в абсолютно збіжному ряді збігаються ряди як з додатних, так і від"ємних членів, а в умовно збіжному ряді обидва вони розбігаються.

Теорема 16. Добуток двох абсолютно збіжних до S і T рядів абсолютно збігається до добутку S·T.

Нехай, например,

- названі абсолютно збіжні ряди. Теорема 16 означає, що

.

На підставі абсолютної збіжності добутку рядів його члени можна записувати різними способами. Зокрема, ми можемо написати

(див. таблицю 1) або краще

( 38 )

(див. таблицю 2).

Розвинення (38) залишається справедливим, якщо тілько один з рядів збігається абсолютно, а другий - просто збігається.

Table 1 Table 2

… … … … ……………………......

Приклад 38. Знайти добуток рядів прикладів 34, 35 , оба з яких абсолютно збігаються на інтервалі .

За теореою 16 шуканий добуток абсолютно збігається на . Запишемо перші чотири члени добутку, впорядковуючи їх за формулою (38) (див. таблицю 2), тобто за зростаючими степенями x,

.

10. Степеві ряди

10.1. Степеневий ряд і властивості його суми

10.1.1. Степеневий ряд, його радіус, інтервал і область збіжності

Ми вже мали справу з функціональними рядами в п. 9.3 (див. Приклади 31 - 35). Зараз ми розглянемо один з найпоширеніших типів функціональних рядів, а саме степеневих.

Означення 1. Степеневим рядом називається функціональний ряд вигляду

, ( 1 )

де дійсні числа

- коефіцієнти, а

- степеневі функції з цілими невід"ємними показниками.

Приклад 1. Ряди

, ,

які ми розглядали в Прикладах 34, 35 попереднього різділу, є степеневими.

Часто-густо розглядають степеневі ряди більш загального вигляду

.( 2 )

Приклад 2. Ряд

,

розглянутий нами в Прикладі 36 того ж розділу, є степеневим вигляду (2).

Ряд (1) є частинним випадком ряду (2) при . З іншого боку, мы можемо звести ряд (2) до вигляду (1), поклавши

,

звідки

.

З цієї причини ми розглядатимемо теорію в основному тільки ряду (1).

Означення 2. Якщо степеневий ряд (1) збігається в точці , тобто збігається числовий ряд

,

то ця точка називається точкою збіжності ряду. Множина всіх точок збіжності називається областю збіжності степеневого ряду.

Аналогічне означення є справедливим для будь-якого функціонального ряду. У випадку степеневого ряду область збіжності має дуже просту структуру, до з"ясування якої ми й переходимо.

Перш за все зауважимо, що степеневий ряд (1) завжди збігається в точці , оскільки набуває в ній вигляду

.

a) Існують степеневі ряди, які збігаються тільки в точці .

Приклад 3. Степеневий ряд

має єдину точку збіжності , оскільки границя (при фіксованому x)

,

і ця границя може бути меншою 1 (а саме, рівною 0) тільки у випадку .

b) Існують степеневі ряди, областю збіжності яких є множина всіх дійсних чисел.

Приклад 4. Степеневий ряд

абсолютно збігається в будь-якій точці x, бо для довільного фіксованого x

і

.

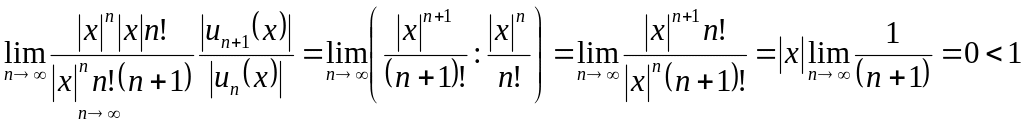c) Існують, нарешті, степеневі ряди, областю збіжності яких є якась частина множини всіх дійсних чисел.

Наприклад, ряди Прикладу 1 збігаються на інтервалах і розбігаються на множинах точок відповідно (див. Приклади 34, 35 попереднього розділу).

Теорема 1 (теорема Абеля¹). Якщо степеневий ряд (1) збігається в точці , то він абсолютно збігається на інтервалі . Якщо він розбігається в точці , то він розбігається поза інтервалом .

■Нехай, наприклад, ряд (1) збігається в точці , тобто збігається числовий ряд

.

На підставі необхідної умови збіжності загальний член цього ряду (а саме ) прямує до нуля при . Отже, для достатньо великих n (нехай для , де N – деяке натуральне число) він є обмеженим: існує число A таке, що

для .

Нехай тепер x – довільна точка інтервалу , тобто , і тому

.

В цьому випадку для загального члена ряду (1) маємо (при )

.

Це означає, що при члени ряду, складеного з абсолютних величин членів ряду (1), менше відповідних членів збіжної геометричної проґресії з знаменником

.

Отже, ряд (1) абсолютно збігається на интервалі .■

З теореми Абеля випливає, що для степеневого ряду (1), який має як точки збіжності, , так і точки розбіжності, існує додатне число R (радіус збіжності) таке, що ряд абсолютно збігається на інтервалі (інтервалі збіжності)

і розбігається поза відрізком .

Поведінку ряду (1) на кінцах інтервалу збіжності завжди треба досліджувати окремо.

Радіуси і інтервали збіжності рядів, згаданих в Прикладі 1, є відповідно . Перший ряд збігається на кінцах інтервалу збіжності, другий же збігається в його правому кінці і розбігається в лівому .

Загальний степеневий ряд (2) завжди збігається в точці . Його інтервал збіжності (у випадку існування точок збіжності і розбіжності) має вигляд

.

Наприклад, радіус і інтервал збіжності ряду, згаданому в Прикладі 2, є відповідно . Ряд збігається на обох кінцях інтервалу збіжності (див. Приклад 35 попереднього роз-ділу).

Якщо степеневий ряд ((1) чи (2)) збігається в єдиній точкі ( або, відповідно, ), ми можемо сказати, що радіус збіжності такого ряду дорівнює нулю, .

Для ряду з Прикладу 3 ми маємо .

У випадку збіжності ряду на множині всіх дійсних чисел ми кажемо, що радіус збіжності є нескінченним, .

Мы маємо в Прикладі 4.

Радіус збіжності степеневого рядку ми можемо шукати таким же чином, як в прикладах 34 - 36 попереднього розділу, тобто за допомогою ознаки Даламбера для ряду, складеного з абсолютних величин членів даного ряду. В одном частинному випадку ми можемо отримати відповідну формулу, а саме

, ( 3 )

якщо границя (3) існує. Дійсно, ознака Даламбера (в тільки що вказананому сенсі) дає

,

і ряд абсолютно збігається при

.

Приклад 5. Для першого з рядів Прикладу 1 маємо

для другого ряду

.

Приклад 6. Для ряду Прикладу 2

.

Приклад 7. Формула (3) незастосовна для ряду

(в цьому випадку ), і ми застосовуємо ознаку Даламбера. Саме, для фіксованого x

.

Ряд абсолютно збігається на множині всіх дійсних чисел, і ми маємо радіус збіжності .

Приклад 8. Довести самостійно, що радіус збіжності ряду

дорівнює нескінченності, .

Заключаючи, ми можемо сказати, що областю збіжності степеневого ряду може бути: a) єдина точка ( для ряду (1) і для ряду (2)); б) множина всіх дійсних чисел; в) деякий інтервал ( для ряду (1) і для ряду (2)), включаючи або виключаючи один чи обидва його кінці.