9.2. Достатні ознаки збіжності числових рядів з додатними членами

Теорема 3 (необхідна і достатня ознака Коші збіжності числового ряду) має велике теоретичне значення, але практичне її застосування часто-густо є занадто складним. Звичайно ми матимемо справу з деякими більш простими до-статніми (але не необхідними) ознаками збіжності. Зупинимось спочатку на числових рядах з додатними членами.

Нехай дано числовий ряд з додатними членами

. ( 18 )

Його часткові суми утворюють зростаючу послідовність

, ( 19 )

і на підставі відповідної теореми про збіжність числової послідовності (див. властивість 6 з п. 1.1.3 А) ми дістаємо наступну теорему.

Теорема 5. Для збіжності ряду з додатними членами достатньо, щоб послідовність його часткових сум була обмеженою зверху.

Іншими словами, якщо існує таке число C, що для всіх натуральних n виконується нерівність

, ( 20 )

то ряд (18) збігається.

Нехай є два ряди з додатними членами, а саме ряд (18) і ряд

. ( 21 )

Теорема 6 (перша ознака порівняння для рядів з додатними членами). Нехай (принаймні для достатньо великих значень n)

(зокрема ). ( 22 )

1. Якщо ряд (21) збігається, то ряд (18) також збігається.

2. Якщо ряд (18) розбігається, то ряд (21) також розбігається.

■Нехай, наприклад, ряд (21) збігається до якогось числа T, тобто існує границя його n-ої часткової суми ,

.

Очевидно,

.

На підставі нерівності (22) (яку можна припустити справедливою для будь-яко-го n) ми для n-ої часткової суми ряду (18) маємо

, .

Отже, послідовність часткових сум ряду (18) є обмеженою зверху числом T, і за теоремою 5 ряд збігається.■

За допомогою теорії границь ми можемо довести наступну теорему.

Теорема 7 (друга ознака порівняння для рядів з додатними членами). Нехай існує границя відношення загальних членів рядів (18) і (21),

. ( 23 )

Якщо k – додатне число ( ), то обидва ряди (18), (21) разом збігаються або ж розбігаються.

Зауваження 1. Для граничних випадків і ми можемо стверд-жувати наступне.

Якщо , то ряд (18) збігається у випадку збіжності ряду (21), а ряд (21) розбігається у випадку розбіжності ряду (18).

Якщо , то ряд (18) розбігається у випадку розбіжності ряду (21), а ряд (21) збігається у випадку збіжності ряду (18).

Для застосування ознак порівняння ми повинні мати деякі стандартні ряди, збіжність або розбіжність яких нам відома. Часто-густо ми використовуємо різні випадки геометричної проґресії (6) і гармонічного ряду (8).

Приклад 13. Дослідити на збіжність ряд

.

Знайшовши загальний член ряду, ми можемо записати його у вигляді

.

Тепер ми порівняємо ряд з збіжним рядом

(геометричною проґресією (6) з знаменником ). Порівняння дає

для будь-якого . На підставі теореми 6 (випадок 1) даний ряд збігається.

Зауваження. Даний ряд можна також порівняти з розбіжним гармонічним рядом

.

Саме, для будь-якого натурального n маємо

.

Але цей результат ні про що не свідчить: в теоремі 6 йдеться тільки про ряди, члени яких не перевищують відповідних членів певного збіжного ряду, або про ряди з членами, не меншими відповідних членів якогось розбіжного ряду. Якщо ж члени одного ряду не перевищують (або просто є меншими) відповідних членів розбіжного ряду, то про перший ряд нічого певного сказати не можна.

Приклад 14. Дослідити на збіжність ряд

.

Помічаючи, що ми порівняємо даний ряд з розбіжним рядом

(гармонічним рядом (7) з ). Порівняння дає

для . На підставі теореми 6 (випадок 2) даний ряд розбігається.

Приклад 15. Щоб дослідити на збіжність ряд

,

ми візьмемо для порівняння збіжний ряд

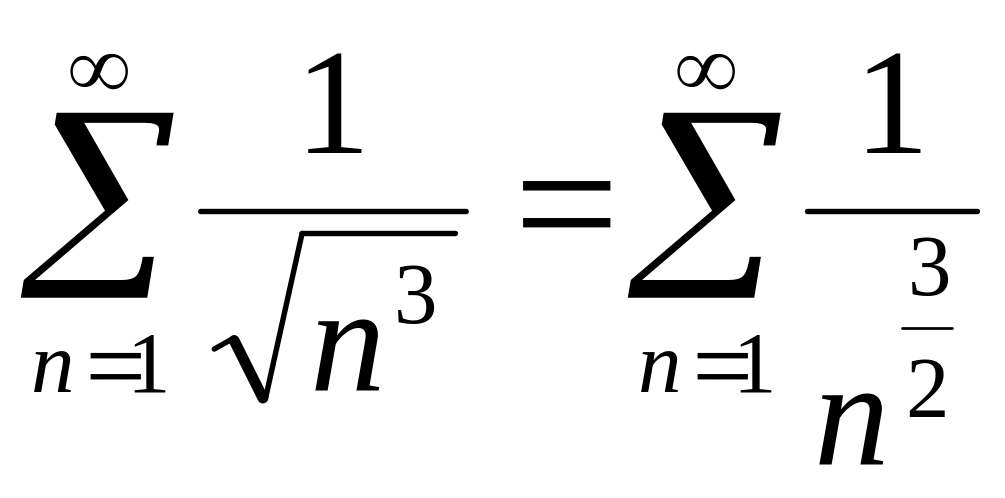
(гармонічний ряд (7) з ) і скористуємось другою ознакою порівняння (теорема 7). Границя відношення загальних членів цих двох рядів дорівнює тобто є додатним числом, а тому даний ряд збігається одночасно з збіжним гар-монічним рядом.

Теорема 8 (ознака Даламбера¹). Якщо для ряду (18) (з додатними членами) існує границя

, ( 24 )

то ряд збігається при і розбігається при . У випадку про поведінку ряду нічого певного сказати не можна (він може як збігатись, так і розбігатись).

■1. Нехай спочатку

.

Згідно з теорією границь для будь-якого існує натуральне число N таке, що для довільного натурального виконуються такі нерівності:

.

Припустимо, що число настільки мале, що Покладаючи послідовно

в нерівності

,

отримаємо

,

,

,

……………………………….

Ми бачимо, що для довільного члени даного ряду менше відповідних членів збіжної геометричної проґресії з знаменником . За теоремою 6 (випадо 1) даний ряд збігається.

2. Нехай тепер

.

В такому випадку для достатньо великих n матимемо

,

звідки видно, що для даного ряду не виконується необхідна умова збіжності (див. теорему 1). Отже, ряд розбігається.■

Приклад 16. Дослідити на збіжність ряд

.

Тут

,

і

.

За ознакою Даламбера ряд збігається.

Приклад 17. Така ж сама задача для ряду

.

Загальний член і наступний член ряду дорівнюють

.

Отже,

Ряд збігається за ознакою Даламбера.

Приклад 18. Дослідити на збіжність ряд

.

.

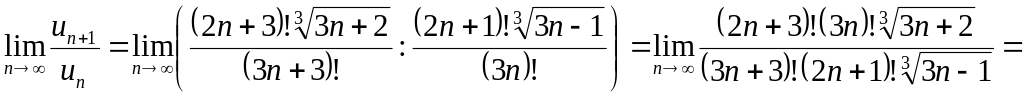
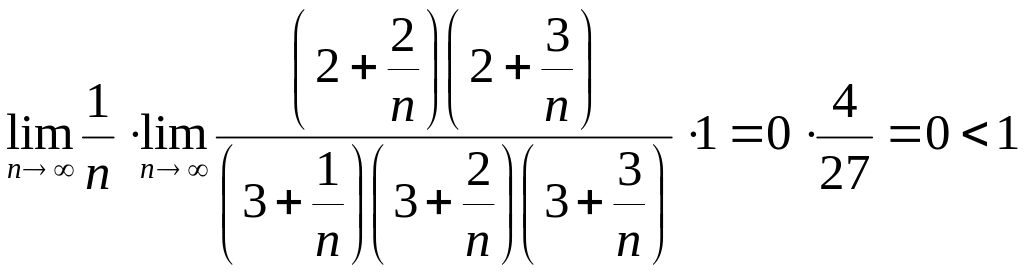Ряд збігається.

Приклад 19. Ознака Даламбера незастосовна до ряді Прикладу 11, тобто до рядів

.

■Для другого ряду

.

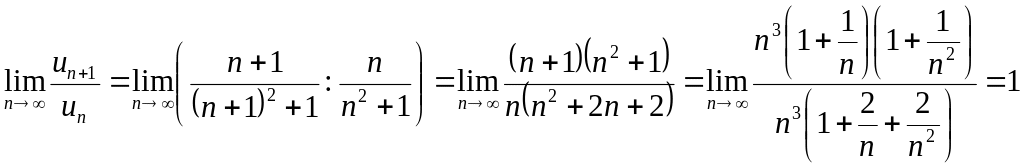Для першого ряду

.■

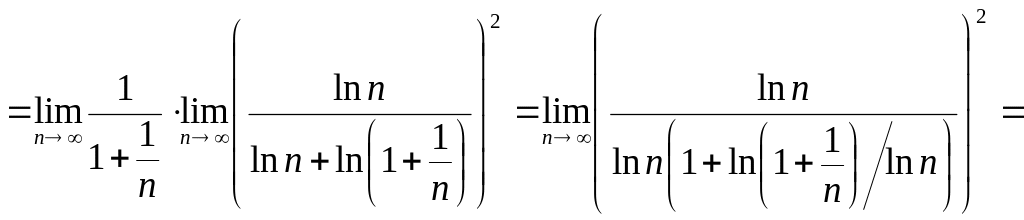
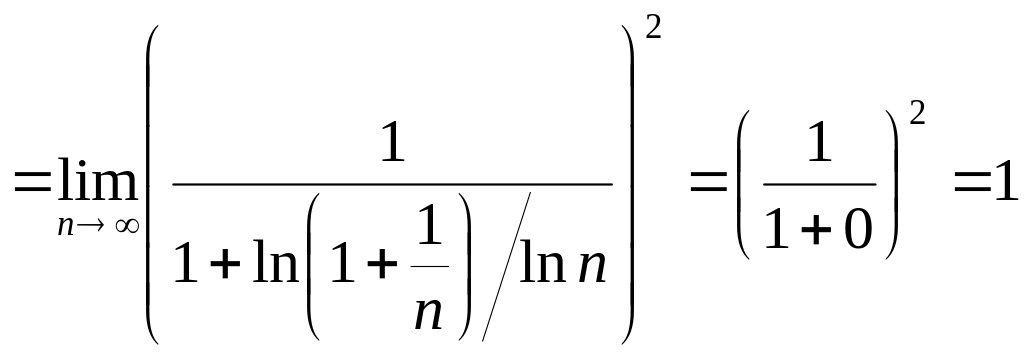Приклад 20. Довести, що для довільного додатного числа a

■Введімо числовий ряд з загальним членом , тобто

.

Він збігається за ознакою Даламбера (перевірте!). Отже, на підставі необхідної умови збіжності границя загального члена ряду при дорівнює нулю.■

Теорема 9 (радикальна ознака Коші). Якщо для ряду (18) (з додатними членами) існує границя

, ( 24 )

то при ряд збігається, а при розбігається. Випадок , аналогічно ознаці Даламбера, є сумнівним.

Приклад 21. Довести збіжність ряду

.

Загальний член ряду

,

і

Ряд збігається за радикальною ознакою Коші.

Корисно зауважити, що

. ( 25 )

■За допомогою правила Лопіталя

.■

Доведіть самостійно, що для довільного натурального m

. ( 26 )

Приклад 22. Ряд

розбігається, оскільки на підставі формули (25)

.

Теорема 10 (інтеґральна ознака Коші). Замінивши n на x в загальному члені ряду (18) (з додатними членами), отримаємо функцію . Якщо ця функція є додатною, неперервною і незростаючою на інтервалі , то ряд (18) і невласний інтеґрал

( 27 )

разом або збігаються, або розбігаються.

■Нехай ; на підставі незростання функції послідов-но мають

. ( 28 )

Покладаючи тепер в нерівності (28) і почленно додаючи всі отримані нерівності, мають

,

або ж

. ( 29 )

1. Якщо інтеґрал (27) збігається, то

.

Внаслідок додатності функції інтеґрал

зростає розом з n, а тому

і на підставі (29) отримаємо

Таким чином, послідовність часткових сум ряду (18) обмежена зверху, і ряд збігається на підставі теореми 5.

2. Якщо тепер збігається ряд (18), то на підставі тієї ж нерівності (29) неважко довести збіжність інтеґрала (27) (завершіть доведення самостійно).■

Приклад 23. Дослідити на збіжність гармонічний ряд (8).

Загальний член ряду

,

і відповідна функція суть

.

Відомо, що невласний інтеґрал

збігається при і розбігається при . Отже, гармонічний ряд (8) збігається при і розбігається при .

Приклад 24. За допомоги інтеґральної ознаки Коші дослідити на збіжність ряди прикладу 11, тобто

a) , b) .

1. Для першого ряду

,

і відповідна функція

є додатною, неперервною і незростаючою на інтервалі . Невласний інте-ґрал

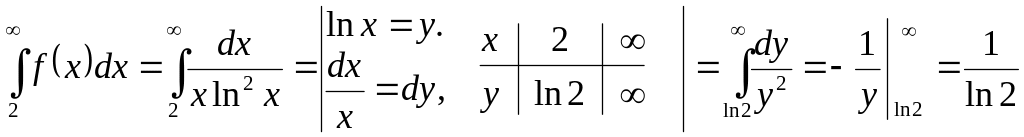
збігається, а тому збігається і ряд a).

2. Другий ряд розбігається, оскільки

,

і невласний інтеґрал

розбігається.

Приклад 25. Застосувати інтеґральну ознаку Коші до ряду

.

Відповідний невласний інтеґрал

збігається, і тому за інтегральною ознакою Коші даний ряд також збігається.