3.1.3. Абсолютні екстремуми

Нехай функція є неперервною на відріз-ку . На підставі теореми 4 з п. 1.2.2 вона набуває на [a, b] своїх найменшого m і найбільшого M значень, тобто існують такі точки , що Рис. 7 , .

Числа називаються абсолютними (іноді кажуть глобальними, тотальними) екстремумами функції на відрізку . Задача полягає в їх знаходженні.

Розв"язуючи задачу на відшукання , ми повинні взяти до уваги, що з двох згаданих точок або принаймні одна знаходиться всередині відрізка, або обидві вони є його кінцями. В першому випадку така внутрішня точка повинна бути, за теоремою Ферма, критичною точкою функції.

На рис. 7 показано графік функції, яка набуває найменшого значення m у внутрішній точці відрізка і найбільшого значення M на його кінці a (тобто ).

На підставі сказаного ми можемо подати наступне

Правило. Щоб знайти найбільше й найменше значення (абсолютні екстремуми) функції, неперервної на відрізку, достатньо:

а) знайти всі її внутрішні критичні точки (тобто ті, які лежать всередині відрізка);

б) знайти значення функції в усіх знайдених точках, а також на кінцях відрізка;

в) з отриманих значень вибрати найбільше та найменше.

Приклад. Знайти найбільше й найменше значення функції на відрізку .

Розв"язання. Функція має дві внутрішні критичні точки (див. попередній приклад). Значення функції в цих точках і на кінцях відрізка дорівнюють

.

Таким чином,

.

3.1.4. Опуклість, угнутість, точки перегину кривих

Означення 4. Крива L називається опуклою, якщо вона лежить нижче дотичної до неї в будь-якій точці кривої (рис. 8 a).

Означення 5. Крива L називається угнутою, якщо вона лежить вище дотичної до неї в будь-якій точці кривої (рис. 8 b).

Означення 6. Точка називається точкою перегину кривої L, якщо вона відокремлює частини опуклості і угнутості кривої (рис. 8 c).

Теорема 6 (достатня умова опуклості графіка функції). Якщо друга похідна функції від"ємна, , на інтервалі , то графік функції є опуклим над цим інтервалом.

Рис. 8

■ Нехай - деяка точка графіка функції , а - дотична до графіка в точці , яка має рівняння

.

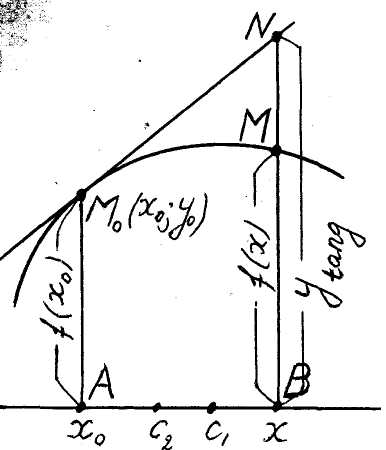
Щоб довести опуклість графіка у випадку , ми повінні довести, що для будь-якого Рис. 9 (рис. 9).

Ми зробимо це в припущенні, що . Двічі застосовуючи теорему Лагранжа, ми отримаємо

Оскільки , ми маємо .■

Зауваження. Достатньою умовою угнутості графіка функції є додатність її другої похідної, .

Зауваження. Опуклість графіка функції в деякому околі точки за умови можна довести за допомоги формули Тейлора для . Дійсно,

.

Теорема 7 (необхідна умова існування точки перегину). Якщо деяка точка є точкою перегину графіка функції , перша похідна якої неперервна в деякому околі точки , то або не існує.

Теорема 8 (достатня умова існування точки перегину). Нехай: а) функція неперервна в точці ; б) або не існує; в) (або ) для ; d) (відповідно ) для . За цих умов точка є точкою перегину графіка функції.

Справедливість теореми є простим наслідком теореми 6.

Приклад. Дослідити функцію

і побудувати її графік.

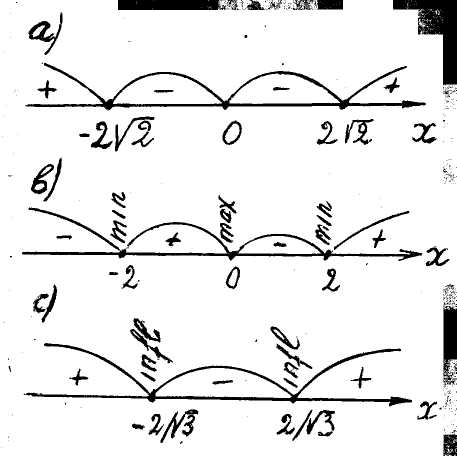
Розв"язок. 1) Областю визначення функції є множина всіх дійсних чисел, . Рис. 10 2) Функція дорівнює нулю в точках , є додатною на і від"ємною на (див. рис. 10 a).

3) Графік функції проходить через точки .

4)  .

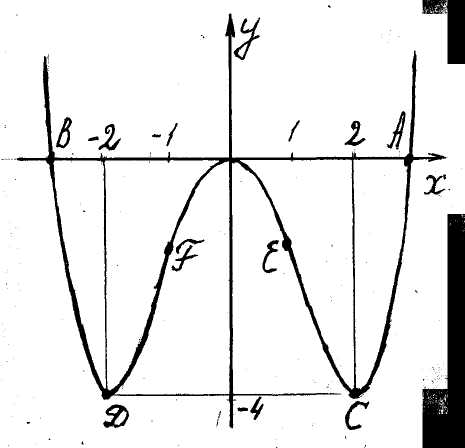
5) . Похідна додатна на , від"ємна на (див. рис. 10b). Отже, функція зростає на , спадає на , має локальний мінімум в точках і локальний максимум 0 в точці . Її графік проходить через точки . Рис. 11 6) . Друга похідна додатна на і від"ємна на . Графік функції угнутий над об"єднанням інтервалів , опуклий над інтервалов (рис. 10 c), має дві точки перегину і .

Графік функції зображено на рис. 11.

Приклад. Дослідити на опуклість, угнутість та існування точок перегину графік функції

,

яку ми вже були розглядали вище.

Розв"язання. Друга похідна функції дорівнює

Вона дорівнює нулю при і не існує при ; на , на інтервалі . Отже, графік функції опуклий над , угнутий над і має дві точки перегину .

Приклад. Довести опуклість еліпса, гіперболи і параболи

, ,

в верхній півплощині (для ).

Розв"язок. У випадку еліпса ми знаємо (п. 3.1.1), що

.

Друга похідна функції є від"ємною у верхній півплощині, а отже еліпс є там опуклим, оскільки

.

Випадки гіперболи і параболи розгляньте самостійно.