
- •Вопросы 1й семестр 1 курс
- •Высказывания. Дизъюнкция. Конъюнция, импликация. Типы теорем. Доказать дизъюнктивную форму импликации. Доказать принцип контрапозиции.
- •1. 3.1. Высказывания
- •Понятие вектора. Линейная зависимость и линейная независимость векторов. Доказать теоремы о линейной зависимости.
- •Вектор (Гиббс) – математический объект, характеризуемый скалярной величиной, направлением и геометрическим характером сложения.
- •Доказать существование и единственность разложения по базису на плоскости и в пространстве.
- •Доказательство:
- •Скалярное произведение. Доказать его свойства.
- •Свойства скалярного произведения:
- •Дистрибутивность: .
- •Векторное произведение. Доказать его свойства.
- •Свойства векторного произведения:
- •Антикоммутативность: .
- •Дистрибутивность:
- •Смешанное произведение. Доказать критерий компланарности векторов.
- •Получить уравнение плоскости и прямой в пространстве.
- •Определение эллипса. Доказать его свойства.
- •Свойства эллипса
- •Доказательство:
- •Определение гиперболы. Доказать ее свойства.
- •Свойства гиперболы
- •Определение параболы. Доказать ее свойства.
- •Свойства параболы
- •Повехности второго порядка. Полчить уравнения цилиндрических поверхностей и поверхностей вращения.
- •3. Двуполостной гиперболоид:
- •Цилиндрические поверхности
- •9 . Гиперболический параболоид
- •Алгебраическая, тригонометрическая и показательная формы комплексного числа. Получить формулу Муавра и формулу извлечения корня n-ой степени из комплексного числа.
- •Решение:
- •Основная теорема алгебры. Доказать ее следствия.
- •Доказательство:
- •Доказательство леммы:
- •Доказательство:
- •Числовые множества, замкнутость. Показать непрерывность действительной оси. Понятие твг и тнг.
- •Бмп. Доказать свойства бмп.
- •Предел числовой последовательности. Доказать единственность предела последовательности.
- •Последовательности бывают:
- •Бмп (бесконечно малые последовательности);
- •3. Неограниченные;
- •Пример. Последовательность ограничена, но не является бмп.
- •Показать существование предела последовательности Бернулли. Число e.
- •Доказать принципы компактности и полноты.
- •Доказать основные теоремы о пределах.
- •Доказать существование первого замечательного предела.
- •Доказать существование второго замечательного предела.
- •Непрерывность функции. Доказать критерий непрерывности.
- •Сравнение функции в окрестности точки. Доказать формулы эквивалентности.
- •Производная функции (определение. Геометрический и физический смысл). Доказать правила дифференцирования.
- •Доказать теоремы о производной композиции функции, производная обратной функции и производной функции, заданной параметрически.
- •Доказать формулы для производных основных элементарных функций.
- •Дифференциал функции. Геометрический смысл производной и дифференциала.
- •Геометрический смысл дифференциала
- •Дифференциал функции
- •Физический смысл дифференциала
- •Первообразная и неопределенный интеграл. Доказать свойства неопределенного интеграла.
- •Доказать теоремы Лагранжа, Коши и Лопиталя.
- •Доказать формулу Тейлора.
- •Монотонность и экстремумы функции. Доказать необходимое и достаточное условие.
- •Выпуклость функци. Доказать необходимое и дотаточное условие для точки перегиба функции.
- •Конструкция определенного интеграла Римана.
- •Доказать свойства определенного интеграла и формулу Ньютона-Лейбница. Не Формула Ньютона-Лейбница
- •Несобственные интегралы первого рода. Признаки сходимости.
- •Несобственные интегралы второго рода. Признаки сходимости.
Цилиндрические поверхности
6.
Эллиптический цилиндр:
.
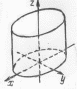 Как
видно из уравнения, плоскости
и
являются плоскостями симметрии данного
цилиндра. Сечение поверхности плоскостью
представляет собой эллипс
.
Сечения цилиндра плоскостями
и
являются парами параллельных прямых
Как
видно из уравнения, плоскости
и
являются плоскостями симметрии данного
цилиндра. Сечение поверхности плоскостью
представляет собой эллипс
.
Сечения цилиндра плоскостями
и
являются парами параллельных прямых
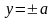 и
и
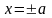 соответственно.
соответственно.
7. Гиперболический цилиндр: .
8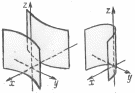 .
Параболический цилиндр
.
.
Параболический цилиндр
.
9 . Гиперболический параболоид
рис.2.655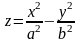 .
Из уравнения вытекает, что плоскости
и
являются плоскостями симметрии. Ось
называется осью гиперболического
параболоида с плоскостью
представляет собой гиперболы
.
Из уравнения вытекает, что плоскости
и
являются плоскостями симметрии. Ось
называется осью гиперболического
параболоида с плоскостью
представляет собой гиперболы
 ,
с полуосями
,
с полуосями
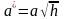 ,
при
,
при
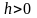 ,
а при
,
а при
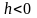 – сопряжённые гиперболы для гипербол
– сопряжённые гиперболы для гипербол
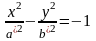 с полуосями
с полуосями
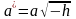 ,
,
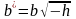 .
.
Заметим,
что плоскость
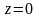 пересекает поверхность по двум прямым
пересекает поверхность по двум прямым
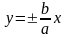 ,
являющихся асимптотами вышеуказанных
гипербол. Сечения плоскостями
и
являются параболами
,
являющихся асимптотами вышеуказанных
гипербол. Сечения плоскостями
и
являются параболами
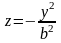 и
и
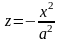 соответственно.
соответственно.
Рассмотрим
примеры поверхностей вращения (вокруг
оси
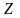 ):
):
Эллипсоид вращения эллипса:
 ,
,
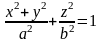 .
.Параболоид вращения параболы:
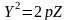 ,
,
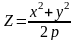 .
.Однополостной гиперболоид получается при вращении гиперболы
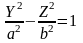 вокруг оси
:
вокруг оси
:
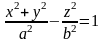 .
.
Алгебраическая, тригонометрическая и показательная формы комплексного числа. Получить формулу Муавра и формулу извлечения корня n-ой степени из комплексного числа.
Комплексным
числом
называется
упорядоченная пара
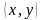 действительных чисел такая, что
выполняются следующие условия. Пусть
действительных чисел такая, что
выполняются следующие условия. Пусть
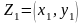 и
и
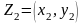 ,
тогда:
,
тогда:
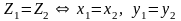 ;
;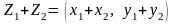 ;
;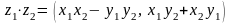 .
.
Число
(первый элемент пары) называется
действительной
частью
числа
,
а
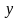 (второй элемент пары) – мнимой
частью.
Обозначим их через
(второй элемент пары) – мнимой
частью.
Обозначим их через
 ,
.
,
.
Запись
комплексного числа в виде
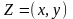 не совсем удобна при выполнении
арифметических операций над комплексными
числами. Поэтому перейдем к алгебраической
форме записи комплексного числа. Пусть
не совсем удобна при выполнении
арифметических операций над комплексными
числами. Поэтому перейдем к алгебраической
форме записи комплексного числа. Пусть
 .
Рассмотрим число
.
Рассмотрим число
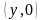 и умножим его на
и умножим его на
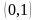 :
:
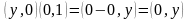 ,
т.е.
,
т.е.
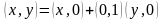 .
.
Используя
введённые обозначения
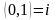 ,
,
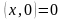 ,
,
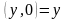 ,
получим:
,
получим:
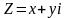 .
Такое представление называют алгебраической
формой
комплексного числа
.
.
Такое представление называют алгебраической
формой
комплексного числа
.
Тригонометрическая:
Мы можем рассматривать полярные
координаты точки, изображающее комплексное
число
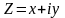 ,
как модуль и аргумент этого числа. Таким
образом,
,
как модуль и аргумент этого числа. Таким
образом,
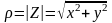 ,
,
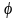 =
=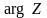 .
Тогда, учитывая
.
Тогда, учитывая
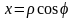 ,
,
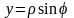 ,
получим тригонометрическую форму числа
:
,
получим тригонометрическую форму числа
:
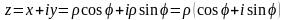 .
.
Пример.
Найти
модуль и аргумент числа
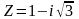 .
.
Решение:
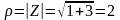
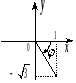 ,
,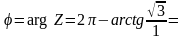 ,
,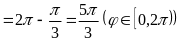 ,
,
рис.
3.10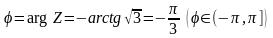
Данная форма комплексного числа удобна для выполнения умножения и деления комплексных чисел, для возведения в степень и извлечение корня n-й степени.
Извлечь
корень n-й
степени из числа
– найти такое число
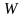 ,
что
,
что
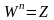 .
.
Пусть
 ,
а
,
а
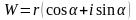 .
Тогда
.
Тогда
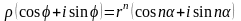 .Отсюда
получим:
.Отсюда
получим:
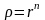 ,
,
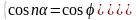 .
.
Решим систему уравнений:
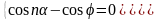
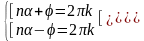 .
.
Таким
образом,
 ,
при
,
при
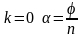 ,
при
,
при
 .
Т.е.
.
Т.е.
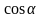 и
и
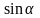 при
при
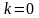 и при
и при
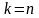 совпадают, и различные корни будут
только при
совпадают, и различные корни будут
только при
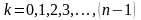 .
Таким образом, решение уравнения
можно записать
.
Таким образом, решение уравнения
можно записать
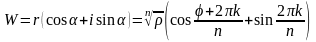 ,
.
Это решение имеет
,
.
Это решение имеет
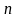 различных значений, которые лежат на
окружности радиуса
различных значений, которые лежат на
окружности радиуса
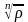 и делят её на
равных частей, каждая из которых
получается поворотом на
и делят её на
равных частей, каждая из которых
получается поворотом на
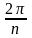 против часовой стрелки относительно
против часовой стрелки относительно
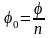 .
.
Замечание.
Обозначение
 не имеет однозначного смысла, поэтому
лучше его избегать.
не имеет однозначного смысла, поэтому
лучше его избегать.
Рассмотрим произведение:
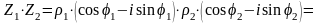
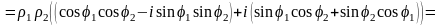
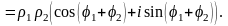
Таким образом, при умножении комплексных чисел модули их перемножаются, а аргументы складываются. Аналогично:
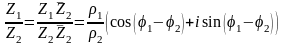 (показать
самостоятельно).
(показать
самостоятельно).
Возведение
числа
в n-ю
степень можно рассмотреть как произведение
одинаковых множителей. Тогда
получим формулу
Муавра:
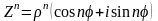 .
.
