
- •1. Кривые в евклидовом пространстве
- •2. Формулы Френе для плоской кривой
- •3. Кривизна кривой. Длина кривой
- •4. Простые поверхности в евклидовом пространстве
- •5. Касательная плоскость
- •6. Длина кривой, заданной на поверхности
- •7. Первая квадратичная форма поверхности
- •8. Главные кривизны поверхности
- •9. Теорема (формула) Стокса
- •10. Теорема (формула) Остроградского
- •11. Скалярные поля. Поверхности уровня
- •12. Производная по направлению
- •13. Градиент скалярного поля
- •14. Оператор Гамильтона (набла-оператор). Правила работы с ним
- •15. Векторные поля. Векторные линии. Поток векторного поля
- •16. Дивергенция векторного поля. Формула Остроградского
- •17. Ротор векторного поля. Формула Стокса
- •18. Потенциальные поля. Условие потенциальности поля.
- •19. Соленоидальные поля. Условие соленоидальности.
- •20. Лапласово поле. Уравнение Лапласа.
- •21. Криволинейные ортогональные координаты
- •22. Коэффициенты Ламэ. Элементы длины кривой, площади поверхности, объема
- •27. Аффинное пространство
- •Определение
- •32. Тензоры в евклидовом пространстве
27. Аффинное пространство
Аффинное пространство — служит обобщением аффинных свойств евклидова пространства. Во многом схоже с векторным пространством, но в отличие от последнего, точки в аффинном пространстве являются равноправными. В частности в аффинном пространстве нет понятия нулевой точки или начала отсчёта. В аффинном пространстве возможно вычитать друг из друга точки и получать векторы так называемого присоединенного пространства; также возможно прибавлять вектор к точке и получать другую точку, но нельзя складывать точки друг с другом
Определение
Аффинное
пространство над полем ![]() —
множество A со свободным
транзитивным действием аддитивной группы векторного
пространства V над
полем
.
—
множество A со свободным
транзитивным действием аддитивной группы векторного
пространства V над
полем
.
Если поле не указывается, то предполагается поле вещественных чисел.
Элементы A называются точками аффинного пространства
Пространство V называется пространством присоединенным к A
Образ действия
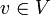 на
на  обозначается a + v
обозначается a + v
Для двух точек
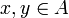 через
через 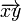 обозначается
такой вектор из V,
что
обозначается
такой вектор из V,
что 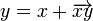
Размерность пространства A определяется равной размерности присоединенного пространства V.
28. Преобразования базиса
29. Ковариантный тензор
30. Контрвариантный тензор
31. Алгебраические операции над тензорами
Тензоры допускают следующие алгебраические операции:
Умножение на скаляр — как и вектор или скаляр (частные случаи тензора);
Сложение тензоров одинаковой валентности и состава индексов (вычислять сумму можно покомпонентно, как и для векторов);
Наличие умножения на скаляр и сложения тензоров делают пространство тензоров одного и того же типа линейным пространством.
Тензорное произведение — без ограничений. Произведением тензора ранга (m,n) на тензор ранга (m',n') является тензор суммарного ранга (m + m',n + n'), то есть если
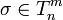 и
и 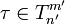 то
их произведение
то
их произведение
![]()
Компоненты тензорного произведения суть произведения соответствующих компонент множителей, например:
![]()
Свёртка тензора — специфическая тензорная операция, понижающая валентность тензора, вычисляется суммированием по паре индексов (верхнего и нижнего, если они различаются) и пробегающих, оставаясь равными друг другу, все свои значения, например:
![]()
(последнее в эйнштейновских обозначениях, где суммирование по повторяющемуся верхнему и нижнему индексу подразумевается автоматически). Часто, если не как правило, свёртка (то есть результат операции свёртки) обозначается той же буквой, что и тензор, к которому свёртка применена, только, конечно, с количеством индексов, на два меньшим.
След матрицы — частный случай свёртки тензора с собой.
Свёртка двух или нескольких тензоров (в том числе тензоров и векторов), например:
![]() (последнее —
в записи
Эйнштейна).
(последнее —
в записи
Эйнштейна).
— операция, которую можно свести к последовательному тензорному умножению этих тензоров (см. чуть ниже) и затем свёртке получившегося тензора (возможно, несколько раз). Очевидно, эта операция линейна по всем входным каналам. Таким образом, свёртка с тензором реализует линейное или полилинейное отображение пространств тензоров на пространство тензоров (в общем случае — на другое), в частности, векторов на векторы и векторов на скаляры.
Свёртка вектора с тензором валентности два есть действие линейного оператора, определяемого этим тензором, на вектор:
![]() (последнее —
в записи Эйнштейна).
(последнее —
в записи Эйнштейна).
Свёртка (однократная) двух тензоров валентности два реализует композицию линейных операторов, определяемых этими тензорами:
![]() (последнее —
в записи Эйнштейна).
(последнее —
в записи Эйнштейна).
Симметризация и антисимметризация — конструирование тензора того же типа с определённым видом симметрии. Для примера, симметризация тензора Tij — это симметричный тензор
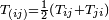 ,
а антисимметризация — антисимметричный
тензор
,
а антисимметризация — антисимметричный
тензор 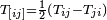 .
В общем случае симметризация по n индексам
имеет вид
.
В общем случае симметризация по n индексам
имеет вид
![]()
а антисимметризация:
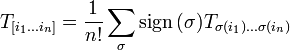
Здесь σ —
всевозможные перестановки индексов ![]() а
а ![]() — чётность
перестановки σ. Разумеется,
не обязательно симметризовать тензор
по всем индексам, здесь это используется
лишь для упрощения записи.
— чётность
перестановки σ. Разумеется,
не обязательно симметризовать тензор
по всем индексам, здесь это используется
лишь для упрощения записи.
Если
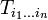 симметричен
по
симметричен
по 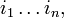 то
симметризация по этим индексам совпадает
с T, а
антисимметризация даёт нулевой тензор.
Аналогично в случае антисимметричности
по некоторым индексам.
то
симметризация по этим индексам совпадает
с T, а
антисимметризация даёт нулевой тензор.
Аналогично в случае антисимметричности
по некоторым индексам.Если
 то
то 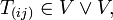
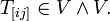 Здесь
Здесь 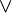 — симметричное,
а
— симметричное,
а 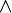 — внешнее произведение
векторных пространств.
— внешнее произведение
векторных пространств.
