Свойства числовых последовательностей.

Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность {y_n} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y1 < y2 < y3 < … < y_n < y_n+1 < ….

Определение. Последовательность {y_n} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y1 > y2 > y3 > … > y_n > y_n+1 > … .

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Пример 1. y1 = 1; y_n = n2\shad \shad0– возрастающая последовательность.

Пример 2. y1 = 1; – убывающая последовательность.

Пример 3. y1 = 1; – эта последовательность не является не возрастающей не убывающей.

Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство y_n = y_n+T . Число T называется длиной периода.

Пример. Последовательность периодична с длиной периода T = 2.

Свойтва числовых множеств

Напомним свойства множества всех действительных чисел .

Множество  – бесконечное, мощности .

; .

Между   и точками числовой оси существует взаимно-однозначное соответствие, поэтому термины "точка" и "действительное число" взаимозаменяемы и, значит, числовые промежутки можно представлять геометрическими отрезками (с концами или без концов).

Если  и   – произвольные действительные числа, то либо , либо , либо ; причем если , то , а также если   и , то .

Для любых различных действительных чисел найдется действительное число "между" ними, например их полусумма, т.е.    или    .

Сформулированное свойство ПЛОТНОСТИ множества  верно и для множеств  и .

Свойство НЕПРЕРЫВНОСТИ ("сплошности") множества  постулируется, например, ПРИНЦИПОМ  КАНТОРА

Для любой последовательности вложенных сегментов

,

с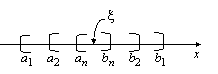 тягивающихся по длине к нулю, т.е. такой, что , существует единственная точка , принадлежащая всем сегментам сразу, т.е. .

Очевидно, что при    Заметим, что хотя  и , но свойство непрерывности для множеств  и  не имеет места.

Ограниченность числовых множеств. Пусть  – произвольное числовое множество, .

( – ограничено сверху) ( );

( – ограничено снизу) ( );

( – ограниченное) ( ), т.е. . Чаще отрезок  берется симметричным относительно , т.е.

( – ограниченное) ( ).

Используя отрицание высказывания, имеем

( – неограниченное) ( ).

Например,  – ограниченное множество, т.к. ;

множество  – неограниченное, так как для   можно указать (существует) , такое, что .

Если множество  ограничено сверху, то говорят: "множество имеет "верхнюю границу", т.е.

.

В этом случае множество всех верхних границ  – бесконечное.

Наименьшая из верхних границ множества  называется точной верхней границей множества  или его ВЕРХНЕЙ ГРАНЬЮ и обозначается  (читается "супремум множества "), т.е.

   ( – верхняя граница множества ;   – наименьшая верхняя граница множества )

или

    .

ПРИМЕРЫ. Множество  имеет множество верхних границ ;  – наибольший элемент множества  и одновременно наименьшая верхняя граница множества, т.е. ,  . Множество  имеет множество всех верхних границ ;  .

Аналогично для ограниченного снизу множества  вводится понятие НИЖНЕЙ ГРАНИ множества  –  (читается "инфимум множества "), как наибольшей из нижних границ множества; ( – точная нижняя граница), т.е.

    .

Покажем по определению . В самом деле, имеем

;

 

.

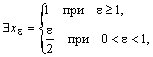
ПРИМЕР. Показать по определению  и  для .

РЕШЕНИЕ. ;

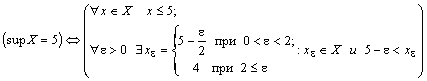
4. Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно n-мерное евклидово пространство обозначается , хотя часто используется не вполне приемлемое обозначение .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

где (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:

,

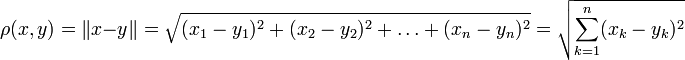где и .

[править] Связанные определения

• Под евклидовой метрикой может пониматься метрика, описанная выше, а также соответствующая риманова метрика.

• Под локальной евклидовостью обычно имеют в виду то, что каждое касательное пространство риманова многообразия есть евклидово пространство со всеми вытекающими свойствами, например, возможностью (по гладкости метрики) ввести в малой окрестности точки координаты, в которых расстояние выражается (с точностью до какого-то порядка) в соответствии с описанным выше.

• Метрическое пространство называют локально евклидовым также если возможно ввести на нём координаты, в которых метрика будет евклидовой (в смысле второго определения) всюду (или хотя бы на конечной области) - каковым, например, является риманово многообразие нулевой кривизны.

[править] Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

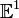• размерности 1 (вещественная прямая)

• размерности 2 (евклидова плоскость)

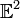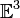• размерности 3 (евклидово трехмерное пространство)

• Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.

Более абстрактный пример:

• пространство вещественных многочленов p(x) степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например )
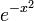