16.2. Метод Фурье (метод разделения переменных) для уравнения вынужденных колебаний струны

Определим закон вынужденных колебаний однородной струны размером l (0<x<l, t>0), для которой в начальный момент времени (при t = 0) заданы начальное смещение равное φ(x) и его скорость равная ψ(x). Один конец струны (х = 0) колеблется по закону μ(t), а второй конец струны (х = l) колеблется по закону ν(t). При этом на струну действует внешняя сила равная f(t). Математически эту задачу можно записать следующим образом

, (16.21)

(16.22)

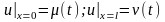. (16.23)

Решение этой задачи будем искать в виде

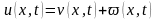(16.25)

где v(t,x) – новая неизвестная функция; ϖ(t,x) – функция, определяемая граничными условиями по следующему правилу

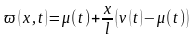. (16.26)

Таким образом, наша задача сводится к нахождению функции v(t,x), для этого необходимо вычислить вторые производные от функции (16.25)

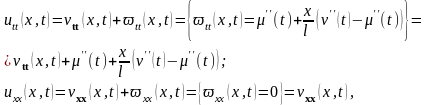(16.27)

и подставив их в исходное уравнение (16.21), получим

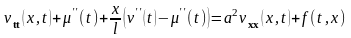
или

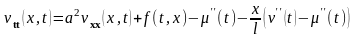
обозначив

,

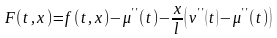получим окончательно

.

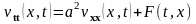Полученное уравнение является уравнением гиперболического типа относительно неизвестной функции v(t,x). Для этого добавим начальные и граничные условия в соответствии с условиями (16.22), (16.23). Запишем первое из начальных условий

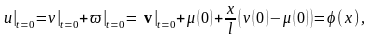
или

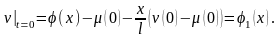
Запишем второе из начальных условий

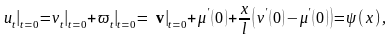
или

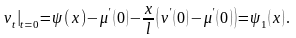
Теперь запишем граничные условия для функции v(t,x).

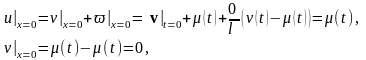
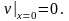
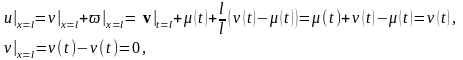
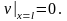
Таким образом, мы перешли от задачи в которой концы струны колеблются каждый по своему закону к задаче с жестко закрепленными концами

; (16.28)

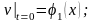
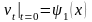; (16.29)

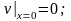(16.30)

Решение этой задачи будем искать в виде

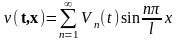. (16.31)

Для нахождения неизвестной функции V_n(t) продифференцируем (16.31) дважды по t и по x

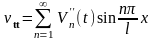, (16.32)

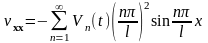, (16.33)

а также разложим функцию F(t,x) в ряд Фурье по синусам

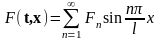, (16.34)

где 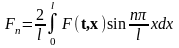. (16.35)

Подставив (16.32), (16.33) и (16.34) в уравнение (16.28), получим

.

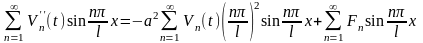В левой и правой частях полученного уравнения имеются одинаковые функции 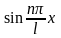, поэтому можно приравнять коэффициенты при этих функциях, в результате получим обыкновенное линейное неоднородное дифференциальное уравнение относительно искомой функции V_n(t)

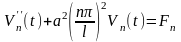. (16.36)

Общее решение этого уравнения состоит из общего решения соответствующего ему однородного уравнения

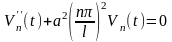(16.37)

и частного решения уравнения (16.36)

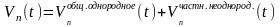. (16.38)

Решение уравнения (16.37) может быть найдено по методу Эйлера. Характеристическое уравнение уравнения (16.37) имеет вид

,

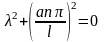следовательно, его корни будут исключительно мнимыми

,

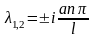Поэтому общее решение уравнения (16.37) можно записать в виде

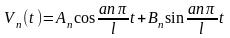. (16.39)

Для нахождения частного решения уравнения (16.36) можно воспользоваться либо методом неопределенных коэффициентов, либо методом Лагранжа (методом вариации произвольной постоянной). Воспользуемся методом Лагранжа. Частное решение 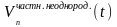уравнения (16.36) будем искать в виде

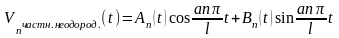. (16.40)

Для нахождения функций A_n(t) и B_n(t) в соответствии с алгоритмом метода составим систему

(16.41)

Решая эту систему, найдем значения коэффициентов A_n(t) и B_n(t). Подставляя найденные коэффициенты в решение (16.40), получим частное решение (16.36). Подставляя (16.38) решение (16.39) и (16.41), получим общее решение уравнения (16.36). Таким образом, подставляя в решение (16.31) найденную функцию V_n(t), найдем искомое решение. Однако в полученном решении еще не определены значения произвольных постоянных A_n(t) и B_n(t). Их конкретные значения найдем, используя начальные условия (16.29) (функци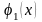и и 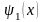предварительно можно разложить в ряд Фурье по синусам на интервале [0,l]). В результате определим вид неизвестной функции v(t,x), подставляя которую в решение (16.25), получим окончательный вид решения исходной задачи.

Рассмотрим еще одну задачу, когда колебания струны с жестко закрепленными концами осуществляются только за счет воздействия внешней силы, действующей по закону

,

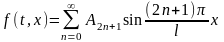поэтому волновое уравнение будет иметь вид

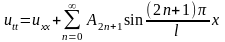. (16.42)

Запишем к нему начальные условия

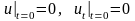, (16.43)

и граничные условия

. (16.44)

Решение такой задачи будем искать в виде

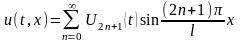. (16.45)

Для нахождения функций U_2n+1(t), продифференцируем дважды по t и x решение (16.45)

,

,

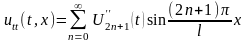и подставим их в исходное уравнение

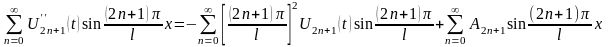
Приравнивая коэффициенты при одинаковых функциях и после преобразования, получим уравнение

.

При различных значениях n,

при n = 0

,

при n = 1

,

…………………………

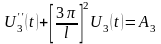и т.д. получим n уравнений для определения функций 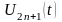. Решение этих уравнений удовлетворим начальным условиям (16.43). Затем подставив полученные функции в решение (16.45), получим окончательное решение исходной задачи.

Пример 16.3. Решить краевую задачу для неоднородного уравнения гиперболического типа

, (П16.3.1)

при начальных условиях

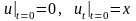(П16.3.2)

и граничных условиях

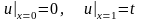. (П16.3.3)

▲ Решение этой задачи будем искать в виде (16.25)

Запишем, чему равна функция ϖ(t,x) в соответствии с граничными условиями (П16.3.3)

,

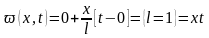Следовательно, функция 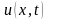принимает вид

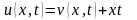. (П16.3.4)

Вычислим от этой функции вторые производные по t и x

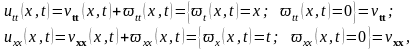
и подставив в исходное уравнение, получим

.

Добавим к этому уравнению начальные

,

,

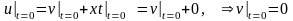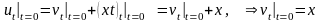и граничные условия

,

.

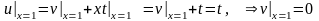Таким образом, получили следующую задачу

; (П16.3.5)

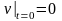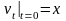, ; (П16.3.6)

, .

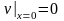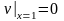Решение этой задачи будем искать в виде (16.31)

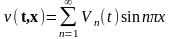. (П16.3.7)

причем

. (П16.3.8)

Вычислим от функции (П16.3.7) вторые производные по t и x и, подставив их в уравнение (П16.3.5), получим

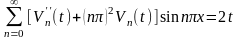. (П16.3.9)

Для нахождения функции V_n(t) разложим единицу в ряд Фурье по системе функций на интервале (0,1):

.

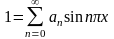Тогда

,

так как

,

то, уравнение (П16.3.9) принимает вид

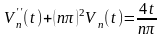, (П16.3.10)

которое является обыкновенным неоднородным линейным уравнением второго порядка. Его общее решение равно сумме общего решения, соответствующего ему однородного уравнения и частного решения неоднородного уравнения (П16.3.10). Общее решение однородного уравнения

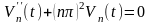
имеет вид

.

Частное решение уравнения (П16.3.10) можно найти, например, методом неопределенных коэффициентов. Сравним вид правой части уравнения (П16.3.10) с выражением

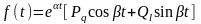(П16.3.11)

и определим значения параметров

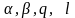
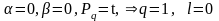
При этих значениях параметров выражение (П16.3.11) имеет вид правой части уравнения (П16.3.10). Следовательно, можно записать частное решение этого уравнения в виде

.

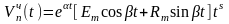Так как 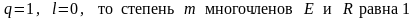, и эти многочлены имеют вид . При наших значениях параметров 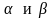комплексное число 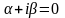равно нулю и не совпадет ни с одним из корней характеристического уравнения 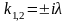, поэтому значение показателя s в формуле равно нулю. Таким образом, частное решение через неопределенные коэффициенты имеет вид

.

Для определения коэффициентов С₁ и С₂, подставим эту функцию в уравнение (П16.3.10)

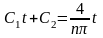. Приравнивая коэффициенты при одинаковых функциях в правой и левой частях этого уравнения, найдем значения неопределенных коэффициентов С₁ и С₂

.

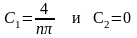Следовательно, частное решение уравнения (П16.3.5) имеет вид

.

Таким образом, общее решение уравнения (П16.3.10) имеет вид

. (П16.3.12)

Используя условие (П16.3.8), найдем значения коэффициентов А_n и В_n:

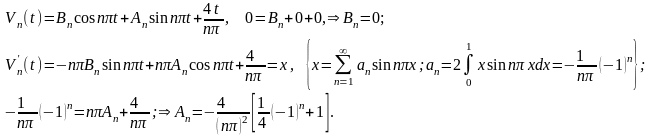Подставляя полученные коэффициенты в формулу (П16.3.12), получим

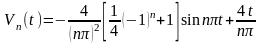. (П16.3.13)

Затем, подставляя (П16.3.13) в решение (П16.3.17), получим

и, используя равенство (П16.3.4) окончательно получим решение исходной задачи:

.▲

Пример 16.4. Решить краевую задачу для неоднородного уравнения гиперболического типа

, (П16.4.1)

при начальных условиях

(П16.3.2)

и граничных условиях

. (П16.3.3)

▲ Понизим степень правой части исходного уравнения

.

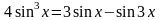Решение этой задачи будем искать в виде (16.45)

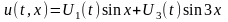. (П16.3.4)

Для нахождения функций U₁(t) и U₃(t), продифференцируем дважды по t и x решение (П16.3.4)

,

,

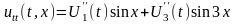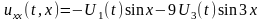и подставим их в исходное уравнение

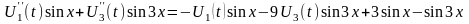
Приравнивая коэффициенты при одинаковых функциях и после преобразования, получим два уравнения

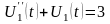, (П16.3.5)

и

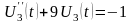. (П16.3.6)

Оба этих уравнения являются обыкновенными линейными неоднородными дифференциальными уравнениями с постоянными коэффициентами. Поэтому их общие решения и представляет собой

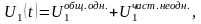(П16.3.7)

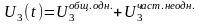. (П16.3.8)

Общее решение однородного уравнения, соответствующего уравнению (П16.3.5) имеет вид

.

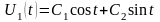Поскольку правая часть уравнения (П16.3.5) является постоянной величиной, то частное решение уравнения (П16.3.5) будет также представлять собой некую постоянную величину

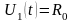. (П16.3.9)

Для того, чтобы найти ее конкретное значение необходимо решение (П16.3.9) подставить в уравнение (П16.3.5)

.

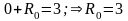Таким образом, общее решение уравнения (П16.3.5) будет иметь вид

.

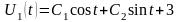Для определения постоянных С₁ и С₂ используем начальные условия (П16.3.2). Удовлетворив первому условию, найдем С₁

.

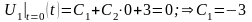Удовлетворив второму условию, найдем С₂

.

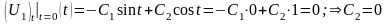Подставляя найденные С₁ и С₂ запишем решение уравнения (П16.3.5)

.

Аналогичным образом решим уравнение (П16.3.6)

.

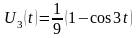Подставляя найденные функции U₁(t) и U₃(t) в решение (П16.3.4), получим решение исходной задачи

.
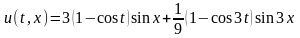