3.2.2. Оценка ошибок квантования

Будем рассматривать квантование с равномерным шагом x=const, т.е. равномерное квантование. Как было отмечено в § 3.1.1. в процессе квантования неизбежно возникает ошибка квантования . Последовательность ошибок квантования (kt), возникающая при квантовании процесса с дискретным временем, называется шумом квантования. Обычно шум квантования предполагают стационарным эргодическим случайным процессом. Чаще всего интерес представляют максимальное значение ошибки квантования, ее среднее значение , равное математическому ожиданию шума и среднеквадратическое отклонение _, равное квадратному корню из дисперсии шума (она характеризует мощность шума квантования). Все эти величины зависят от способа округления, применяемого при квантовании, кроме того и _ зависят от закона распределения w() мгновенных значений сигнала в пределах шага квантования. Считая шаг квантования x малым по сравнению с диапазоном изменения сигнала, плотность w(x) в пределах этого шага можно принять равномерной, т.е. . Различают квантование с округлением, с усечением и с усечением модуля. При квантовании с округлением истинному значению отсчета приписывает ближайший разрешенный уровень квантования независимо от того, находится он сверху или снизу. Очевидно, что при этом

max=0.5x;

(3.31а)

Квантование с округлением требует определенной сложности в реализации. Проще выполняется квантование с усечением, при котором истинному значению отсчета приписывается ближайший нижний уровень. При этом

max=x;

т.е. максимальное значение погрешности в 2 раза больше, а , что приводит к накоплению погрешности квантования при дальнейшей обработке квантованной последовательности. Промежуточное положение по точности и сложности реализации занимает квантование с усечением модуля, которое для положительных отсчетов является таким же, как и квантование с усечением. Отрицательным отсчетам приписывается ближайший верхний уровень. При этом то есть накопление погрешностей не происходит, но в 2 раза увеличивается максимальная погрешность, и в 2 раза - мощность шума квантования . Выбирая достаточно большее число уровней квантования N, шаг квантования. , а следовательно и все рассмотренные погрешности можно сделать необходимо малыми. При неравномерном законе распределения мгновенных значений сигнала квантования с постоянным шагом не является оптимальным по критерию минимума среднеквадратической ошибки . Квантуя участки с менее вероятными значениями сигнала с большим шагом значение можно уменьшить, при этом же количестве уровней квантования.

3.3. Информация в непрерывных сообщениях

Для того, чтобы оценить потенциальные возможности передачи сообщений по непрерывным каналам, необходимо вести количественные информационные характеристики непрерывных сообщений и каналов. Обобщим с этой целью понятие энтропии и взаимной информации на ансамбли непрерывных сигналов. Пусть Х - случайная величина (сечение или отсчет случайного процесса), определенная в некоторой непрерывной области и ее распределение вероятностей характеризуется плотностью w(х). Разобьем область значений Х на небольшие интервалы протяженностью x. Вероятность Р_к того, что х_к<x<x_к+ x, приблизительно равна w(х_к) x т.е.

Рк=Р( хк<x<xк+x)  w(хк)x,

(3.32)

причем приближение тем точнее, чем меньше интервал x. Степень положительности такого события. Если заменить истинные значения Х в пределах интервала x значениями х_к в начале интервала, то непрерывный ансамбль заменится дискретным и его энтропия в соответствии с (1.4) определится, как или с учетом (3.32)

(3.33)

Будем теперь увеличивать точность определения значения х, уменьшения интервал x. В пределе при x0 получим энтропию непрерывной случайной величины.

(3.34)

Второй член в полученном выражении стремится к и совершенно не зависит от распределения вероятностей Х. Это означает, что собственная информация любой непрерывной случайной величины бесконечно велика. Физический смысл такого результата становиться понятным, если учесть, что в конечном диапазоне непрерывная величина может принимать бесконечное множество значений, поэтому вероятность того, что ее реализация будет точно равна какому-то наперед заданному конкретному значению является бесконечно малой величиной 0. В результате энтропия, определенная в соответствии с (1.4), характеризующая среднюю степень неожиданности появления возможных реализаций для любой непрерывной случайной величины не зависит от ее закона распределения и всегда равна бесконечности. Поэтому для описания информационных свойств непрерывных величин необходимо ввести другие характеристики. Это можно сделать, если обратить внимание на то, что первое слагаемое выражении (3.34) является конечным и однозначно определяется плотностью распределения вероятности w(x). Его называют дифференциальной энтропией и обозначают h(x):

(3.35)

Дифференциальная энтропия обладает следующими свойствами.

1. Дифференциальная энтропия в отличии от обычной энтропии дискретного источника не является мерой собственной информации, содержащейся в ансамбле значений случайной величины Х. Она зависит от масштаба Х и может принимать отрицательные значения. Информационный смысл имеет не сама дифференциальная энтропия, а разность двух дифференциальных энтропий, чем и объясняется ее название. 2. Дифференциальная энтропия не меняется при изменении всех возможных значений случайной величины Х на постоянную величину. Действительно, масштаб Х при этом не меняется и справедливо равенство

(3.36)

Из этого следует, что h(x) не зависит от математического ожидания случайной величины, т.к. изменяя все значения Х на С мы тем самым изменяем на С и ее среднее, то есть математическое ожидание. 3. Дифференциальная энтропия аддитивна, то есть для объединения ХY независимых случайный величин Х и Y справедливо: h(XY)= h(X)+ h(Y). Доказательство этого свойства аналогично доказательству (1.8) аддитивности обычной энтропии. 4. Из всех непрерывных величин Х с фиксированной дисперсией ² наибольшую дифференциальную энтропию имеет величина с гауссовским распределением, т.е.

(3.37)

Доказательство свойства проведем в два этапа: сначала вычислим h(x) для гауссовского распределения, задаваемого плотностью. где м - математическое ожидание, а затем докажем неравенство (3.37). Подставив (3.38) в (3.35) найдем< Для доказательства неравенства (3.37) зададимся произвольным распределением (х) с дисперсией ² и математическим ожиданием m и вычислим интеграл J вида

Но в силу неравенства (1.7) с учетом правила изменения основания логарифмов (log t = log e  ln t) имеем:

так как подинтегральное выражение - гауссовская плотность распределения см.(3.38).

Таким образом , откуда . Но как только что было показано, - это дифференциальная энтропия гауссовского распределения. Доказанное неравенство и означает, что энтропия гауссовского распределения максимальна. Попытаемся теперь определить с помощью предельного перехода взаимную информацию между двумя непрерывными случайными величинами X и Y. Разбив области определения Х и Y соответственно на небольшие интервалы x и y, заменим эти величины дискретными так же, как это делалось при выводе формулы (3.34). Исходя из выражения (1.14) можно определить взаимную информацию между величинами Х и Y .

(3.39)

При этом предельном переходе никаких явных бесконечностей не появилось, т.е. взаимная информация оказывается величиной конечной, имеющей тот же смысл, что и для дискретных сообщений. С учетом того, что

(x,y)= (y)  (x/y)

равенство (3.39) можно представить в виде

(3.40)

Здесь h(X) - определенная выражением (3.35) дифференциальная энтропия Х, а

(3.41)

h(X/Y) - условная дифференциальная энтропия. Можно показать, что во всех случаях h(X/Y)h(X). Формула (3.40) имеет ту же форму, что и (1.13), а отличается лишь заменой энтропии дифференциальной энтропией. Легко убедиться, что основные свойства 1 и 2 (см. пункт 1.3) взаимной информации, описываемые равенствами (1.15)(1.17), остаются справедливыми и в этом случае.

3.4 -энтропия и -производительность источника непрерывных сообщений

Как было показано в § 3.3, в одном отсчете любого непрерывного сообщения содержится бесконечное количество собственной информации. И тем не менее, непрерывные сообщения (телефонные разговоры, телепередачи) успешно передаются по каналам связи. Это объясняется тем, что на практике никогда не требуется абсолютно точного воспроизведения переданного сообщения, а для передачи даже с очень высокой, но ограниченной точностью, требуется конечное количество информации, также как и при передаче дискретных сообщений. Данное обстоятельство и положено в основу определения количественной меры собственной информации, источников непрерывных сообщений. В качестве такой меры, принимается минимальное количество информации, необходимое для воспроизведения непрерывного сообщения с заданной точностью. Очевидно, что при таком подходе собственная информация зависит не только от свойств источника сообщений, но и от выбора параметра , характеризующего точность воспроизведения. Возможны различные подходы к определению  в зависимости от вида и назначения передаваемой информации. Наиболее часто в информационной технике в качестве  используют среднеквадратическое отклонение между принятым у и переданным х сигналами, отражающими непрерывные сообщения, т.е.

,

(3.42)

где Х и Y – ансамбли сигналов, отражающих исходное и воспроизведенное сообщения. Два варианта сообщения или сигнала, различающиеся не более, чем на заданное значение ₀, называются эквивалентными. Взаимная информация I(X,Y) между двумя эквивалентными процессами X(t) и Y(t) может быть определена в соответствии с (3.40) как

I(X,Y)=h(X)-h(X/Y),

где h(X) и h(X/Y) – соответственно дифференциальная и условная дифференциальная энтропии. Из приведенного выражения видно, что величина I(X,Y) зависит не только от собственного распределения (х) ансамбля Х (см. (3.35)), но и от условного распределения (x/y) (см. (3.41)), которое определяется способом преобразования процесса X в Y. Для характеристики собственной информации, содержащейся в одном отсчете процесса Х, нужно устранить ее зависимость от способа преобразования сообщения Х в эквивалентное ему сообщение Y. Этого можно добиться, если под количеством собственной информации или  - энтропией H_(Х) процесса Х понимать минимизированную по всем распределениям (X/Y) величину I(X,Y), при которой сообщения Х и Y еще эквивалентны, т.е.

.

(3.43)

Таким образом,  - энтропия определяет минимальное количество информации, содержащейся в одном отсчете непрерывного сообщения, необходимое для воспроизведения его с заданной верностью. Если ансамбль сообщений Х представляет собой процесс с дискретным временем с непрерывными отсчетами, то под  - производительностью источника понимают величину

,

(3.44)

где _с – количество отсчетов сообщения, выдаваемых в единицу времени. В том случае, когда Х - непрерывный случайный процесс с ограниченным спектром, вся информация, содержащаяся в его значениях, эквивалентна информации, содержащейся в отсчетах процесса, следующих друг за другом с интервалом , (f_m-граничная частота спектра), т.е. со скоростью

c=2 m.

(3.45)

При этом  - производительность источника или процесса по-прежнему определяется выражением (3.44), где величина _с рассчитывается из условия (3.45). В том случае, если следующие друг за другом отсчеты процесса коррелированны (взаимозависимы), величина Н_(Х) в (3.43) должна вычисляться с учетом вероятностных связей между отсчетами. Итак,  - производительность источника непрерывных сообщений представляет собой минимальное количество информации, которое нужно создать источнику в единицу времени, для воспроизведения его сообщений с заданной верностью.  - производительность называют также скоростью создания информации при заданном критерии верности. Максимально возможная  - производительность непрерывного источника Х обеспечивается при гауссовском распределении Х с дисперсией (при этом условии h(X) максимальна (см. (3.37)). Оценим значение . Рассмотрим случай, когда непрерывное сообщение X(t) представляет собой стационарный гауссовский процесс с равномерным энергетическим спектром, ограниченным частотой F_c, и с заданной мощностью (дисперсией) Р_х, а критерий эквивалентности  задан в виде (3.42). Будем считать, что заданная верность воспроизведения обусловлена действием аддитивной статистически не связанной с сигналом помехи (t) с математическим ожиданием М[]=0 и дисперсией (мощностью) . Исходный сигнал Х рассматриваем как сумму воспроизводящего сигнала Y и помехи:

X=Y+.

При этом, поскольку (x/y)= (y+/y)= (/y)= (), то h(X/Y) полностью определяется шумом воспроизведения (t). Поэтому max h(X/Y)=max h(). Так как шум воспроизведения имеет фиксированную дисперсию , то дифференциальная энтропия имеет максимум (3.37) при гауссовском распределении шума

.

В свою очередь дифференциальная энтропия гауссовского источника с дисперсией .

.

Следовательно,  - энтропия на один отсчет сообщения

(3.46)

Величина характеризует минимальное отношение сигнал-шум, при котором сообщения X(t) и Y(t) еще эквивалентны. Согласно теореме Котельникова шаг дискретизации , а _c=2 F_c. При этом равномерность спектра сообщения обеспечивает некоррелированность отстоящих на t друг от друга отсчетов, а гауссовский характер распределения X(t) - их независимость. Следовательно, в соответствии с (3.44)

,

или с учетом (3.46)

.

(3.47)

Количество информации, выданное таким источником за время Т_с

.

(3.48)

Интересно отметить, что правая часть выражения (3.48) совпадает с наиболее общей характеристикой сигнала, называемой его объемом, если принять динамический диапазон сигнала D=log  ₀. Это означает, что объем сигнала равен максимальному количеству информации, которое может содержаться в сигнале длительностью Т_с.
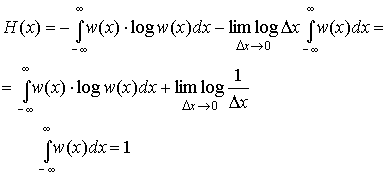
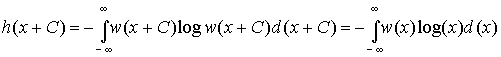
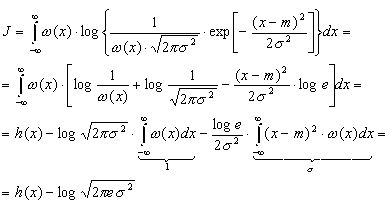
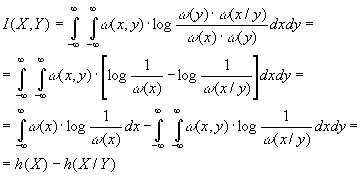
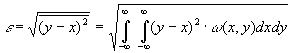