
- •Глава 1. Развитие понятия функции.
- •Глава 2. Основные свойства функции.
- •2.1. Четные и нечетные функции
- •2.2. Монотонность функции
- •2.3. Экстремумы функций
- •2.4. Выпуклость функций
- •2.5. Асимптоты
- •2.7. Нули функций
- •2.8. Периодическая функция
- •Глава 4. Построение графиков функций.
- •Глава 5. Примеры задач
- •Глава 6. Задачи:
Глава 4. Построение графиков функций.
При построении графика функции можно придерживаться следующего плана.
1) Найти область определения функции. Выяснить, является ли функция четной (нечетной), периодической.
2) Найти точки пересечения графика с осями координат и промежутки.
3) Найти асимптоты графика.
4) Сделать эскиз графика.
5) Вычислить, найти экстремумы и промежутки возрастания (убывания) функции.
6) Вычислить, найти точки перегиба и промежутки выпуклость вогнутость функции.
7) Нарисовать график функции.
Глава 5. Примеры задач
1) Построить
график функции.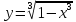
1) Область
определения — вся ось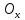 , т.е. .D(y)=
, т.е. .D(y)=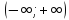
2) Функция не является четной или нечетной.
3) Точки пересечения с осями координат: еслиx=0 , то y=1 ; если y=0 , то x=1
4) Точек разрыва и вертикальных асимптот нет. Имеем:
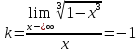
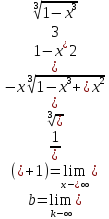
И так, наклонная
асимптота![]() .
.
5) Находим
y’=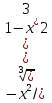 ;y’=0 при
;y’=0 при
![]() ;y’=
;y’=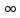 при x=1 . В окрестности
критических точек производная не меняет
знака, экстремумов нет. Так как
при x=1 . В окрестности
критических точек производная не меняет
знака, экстремумов нет. Так как
![]() при всех
при всех
![]() ,
то функция убывает на всей числовой
оси.
,
то функция убывает на всей числовой
оси.
6) Находим
y”=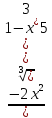 ; y”=0при
; y”=0при
![]() ;
y”=
;
y”=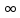 при x=1 ;y”(-h)
при x=1 ;y”(-h)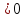 ;y”(h)
;y”(h)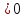 ,y”(1-h)
,y”(1-h)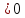 ; y”(1+h)
; y”(1+h)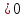 .
Следовательно, в промежутках
.
Следовательно, в промежутках
![]() и
и
![]() кривая вогнута, а в промежутке - -
выпукла. Точки перегиба имеют координаты
и .
кривая вогнута, а в промежутке - -
выпукла. Точки перегиба имеют координаты
и .
Используя полученные данные, строим искомый график:
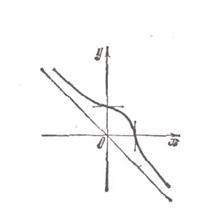
2) y = x ^3 + 2x^2 - x - 2 и постройте график.
Решение . Исследуем функцию по вышеприведенной схеме.
-
область определения x
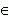 R
( x
– любое действительное число);
R
( x
– любое действительное число); -
область значений y
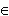 R,
так как f
( x
) – многочлен нечётной степени;
R,
так как f
( x
) – многочлен нечётной степени; -
функция f ( x ) не является ни чётной, ни нечётной
-
f ( x ) – непериодическая функция
-
график функции пересекается с осью Y в точке ( 0, – 2 ),
-
так как f ( 0 ) = - 2 ; чтобы найти нули функции нужно
-
решить уравнение: x^ 3 + 2x ^2 - x - 2 = 0, один из корней
которого ( x = 1 ) очевиден. Другие корни находятся
из решения квадратного уравнения:
X^2 + 3x + 2 = 0, которое получено делением многочлена
X^ 3 + 2x^ 2 - x - 2 на двучлен ( x – 1 ). Легко проверить,
что два других корня: x2 = -2 и x3 = -1. Таким образом,
нулями функции являются: -2, -1 и 1.
Это значит, что числовая ось делится этими корнями на
четыре интервала знакопостоянства, внутри которых
функция сохраняет свой знак:
![]()
Этот результат может быть получен разложением
многочлена на множители:
x^ 3 + 2x ^2 - x - 2 = ( x + 2 ) ( x + 1 ( x – 1 )
и оценкой знака произведения методом интервалов
Производная f’ ( x ) = 3x^2 + 4x -1 не имеет точек, в которых
она не существует, поэтому её область определения R ( все
действительные числа); нули f’ ( x ) – это корни уравнения:
3x^2 + 4x - 1 = 0 .
Эти корни
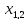 =-4
=-4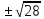 /6=
/6=
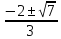 функция имеет две критич. точки и три
интервала монотонности (-
функция имеет две критич. точки и три
интервала монотонности (- ;
;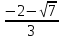 ),
(
),
(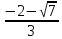 ,
,
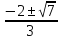 )
и (
)
и (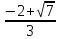 , +
, +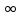 )
)
Полученные результаты сведены в таблицу
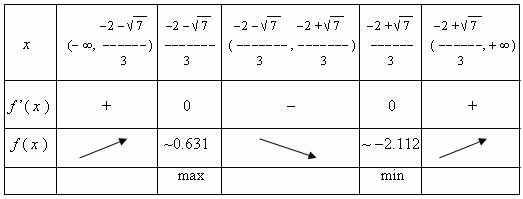

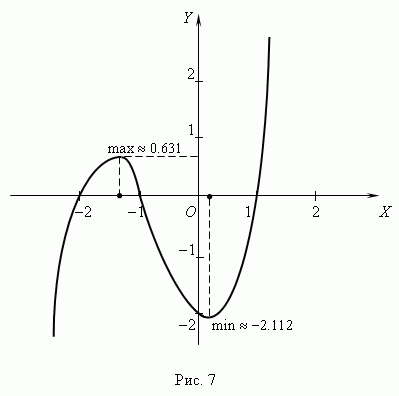
3) Исследовать функции и построить их графики.
y=x/1+x^2.
Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: x = 0,у=0.
Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).
y’=1+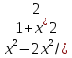 =
=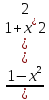
Критические точки: x1 = 1; x2= –1.
Ymin=f(-1)=-1/2
Ymax=f(1)=1/2
![]()
y”=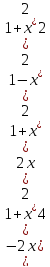 =
=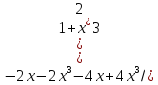 =
=
2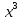 -6x
/ (1+
-6x
/ (1+ ;
;
2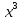 -6x/
(1+
-6x/
(1+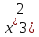 =0,
x1=0, x2=-
=0,
x1=0, x2=-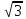 ,
x3=
,
x3=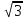
F(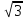 )=-
)=-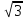 /
4
/
4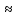 0,4
0,4
а) Вертикальных асимптот нет
x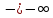 :
k=
:
k=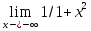 =0,
b=0, y=0
=0,
b=0, y=0
x-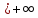 :
k=
:
k=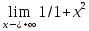 =0,
b=
=0,
b=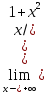 =0
=0
б) Асимптота – y = 0.
![]()
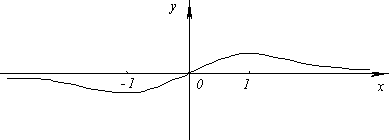
4) Исследовать
функции и построить их графики y=2x-3
D(y)=(–∞; +∞). Точек разрыва нет
2x-3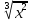 =0
x1=0, x2=3
=0
x1=0, x2=3
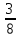
Пересечение с осью Ox:
y’=2-3 =
=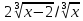 ;
x1=0, x2=1;
ymin=f(1)=-1,
ymax=f(0)=0;
;
x1=0, x2=1;
ymin=f(1)=-1,
ymax=f(0)=0;


а) Вертикальных асимптот нет.
x-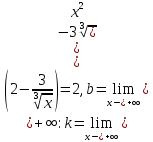 =-
=-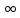 ;
x-
;
x-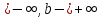
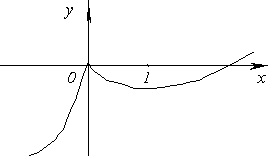
Наклонных асимптот нет.
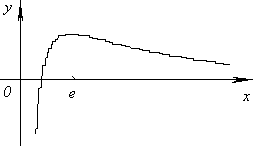
5) Исследовать функции и построить их графики y= lnx/x.
D(y)=(0; +∞). Функция непрерывна на области определения.
Пересечение
с осью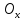 :
:
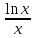 =0,
x=1
=0,
x=1
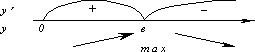
y’=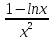 ;
x=e; ymax=f(e)
;
x=e; ymax=f(e)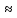 0,4
0,4
y”=-x-2x(1-lnx)/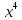 =
=
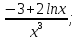 x=
x=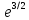
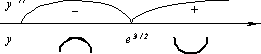
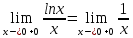 lnx=
lnx=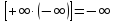
Вертикальная асимптота x = 0.
x-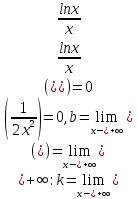
Наклонная асимптота y = 0
