Урок-повторение по теме "Тригонометрические уравнения и неравенства" (11-й класс)

Медведева Надежда Степановна, учитель математики и информатики

Статья отнесена к разделу: Преподавание математики

Цели:

• Образовательные – систематизировать  знания и создать разноуровневые условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.

• Развивающие – способствовать  формированию умений применять полученные знания в новой ситуации, развивать математическое мышление, речь.

• Воспитательные – содействовать  воспитанию интереса к математике, активности, мобильности, умения общаться.

Ход урока

1. Оргмомент

2. Математическая эстафета

3. Конкурс капитанов

4. Самостоятельная работа

5. Угадай слово

6. Подведение итогов. Домашнее задание

I. Оргмомент

Сегодня на уроке мы повторим тему «Тригонометрические уравнения и неравенства». Тем самым систематизируем  знания и создадим разноуровневые условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений. Данная тема важна еще и тем, что тригонометрические уравнения встречаются в заданиях ЕГЭ во всех частях.

(Приложение 1)

Рассадить учащихся по группам (их две), выбрать капитанов. Четырех учеников посадить за компьютеры для решения тестов. Одному ученику дать индивидуальное задание: решить уравнение, входящее в часть В тестов ЕГЭ.

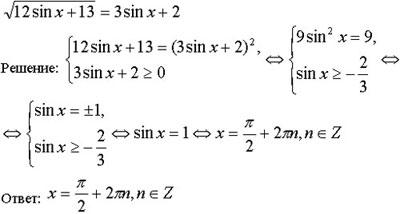
II. Математическая эстафета (Приложение 3)

Данный этап позволит нам отработать все формулы тригонометрических уравнений.

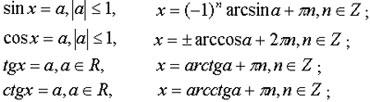
Члены команды по очереди подходят к доске и решают очередное уравнение.

Задания для 1 команды (Приложение 2)

Задания для 2 команды

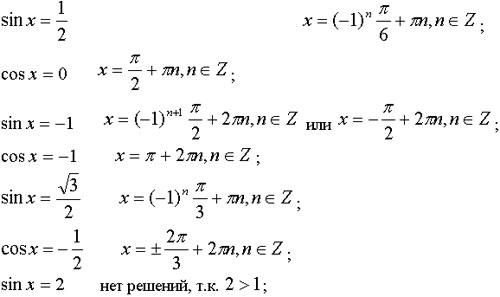
III. Конкурс капитанов

Пока капитаны у доски решают свои задания, проверим ученика с индивидуальным заданием: решить уравнение, входящее в часть В тестов ЕГЭ.

1 капитану решить уравнение (1 - cos2x)(tgx - √3) = 0

Решение:

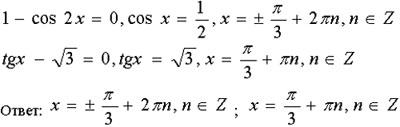
2 капитану решить уравнение (1 - 2sinx)(ctgx - 1) = 0

Решение:

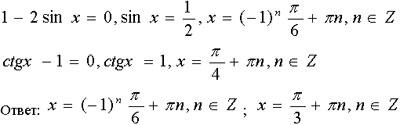
IV. Самостоятельная работа

Каждая группа получает карточку, в которой не только задания работы, но и карточка со вспомогательной консультацией по решению каждого задания.

Задание группе №1

1. Решите уравнение:

а) 2cos²x+ 3cosx+ 1 = 0

б) sin²x + √3sinx ∙ cosx = 0

2. Решите неравенство:

tg3x< -1.

3. Решите систему:

4. Решите неравенство:

│2 sin x + 4│≤5

Дополнительно:

1. Решите уравнение:

√3sin x+cos x= -1.

2. Решите неравенство:

2 cos²x+cos x- 1 ≤ 0.

3. Решите уравнение:

5 sin x - 6 cos x= 6.

Группа №1

Консультация первого уровня.

1. а) Решите уравнение относительно cos х по общей формуле для корней квадратного уравнения, после чего получившееся уравнение решите относительно х.

б) Разложите левую часть уравнения на множители и примените условие равенства произведения нулю.

2. Запишите решение неравенства относительно аргумента “3х”, а дальше относительно “х”.

3. Решите систему способом подстановки.

4. Исследуйте знак выражения, стоящего под знаком модуля.

Консультация второго уровня.

1. а) Решите уравнение как квадратное относительно cos x, придете к совокупности уравнений cos x= -(1/2) и cos x= -1. Решая каждое из уравнений, учтите, что arсcos(-1/2) = 2π/3, а второе уравнение можно решать используя частный случай.

б) Имеем: sin x (sin x +√3cos x) = 0. Перейдем к совокупности  уравнений sin x = 0; sin x+√3cos x= 0. Решаем как однородное уравнение I степени (деление обеих частей уравнения на cos x≠ 0 или на sin x≠ 0).

2. Имеем: -(π/2) + πn< 3x< -(π/4) + πn, n ∈Z. Решаем двойное неравенство относительно x.

3. Выразив из 1-го уравнения x= π + y и подставив во 2-ое уравнение, получим sin(π + 2y) = -1.

Запишем решение относительно (π + 2y) учитывая частный случай, затем  выразим y.

4. Проанализировав подмодульное выражение имеем, что оно положительно для любого x. Переходим к решению неравенства 2sin x+ 4 ≤ 5 sinx ≤ 1/2. Решив его, получаем:

Консультации для дополнительных заданий первого уровня.

1. Умножьте обе части уравнения на 1/2.

2. Введите замену: cos x= y и решите квадратное неравенство.

3. Воспользуйтесь формулами sin x= 2 sin(x/2)cos(x/2)

cos x + 1 = 2cos²(x/2)

Консультации для дополнительных заданий второго уровня.

1. Заметим, что √3/2 = cos(π/6); 1/2 = sin(π/6). Имеем формулу sin(π/6 + x) в левой части уравнения. Решаем уравнение: sin(π/6 + x) = -(1/2)

2. Имеем: 2y² + y – 1 ≤ 0

y ∈[-1; 1/2]

-1 ≤ cos x ≤1/2

Решаем графически на единичной окружности.

3. Имеем

5 sin x - 6 cos x - 6 = 0

5 sin x - 6(cosx + 1) = 0

10 sin(x/2)cos(x/2) - 6 ∙ 2cos²(x/2) = 0

Вынесем общий множитель за скобки. Будем решать совокупность уравнений:

cos(x/2) = 0 или sin(x/2) - 1,2cos(x/2) = 0        

(имеем однородное уравнение I степени)

cos(x/2) ≠ 0.

Задание группе № 2

1. Решите уравнение:

а) tgx+ ctgx= 2;

б) 2 sin²x + 5 sinx ∙ cosx - 7cos²x = 0.

2. Решите неравенство:

cos (π/2 + x) < - 0,5√3

3. Решите систему:

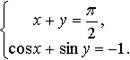
4. Решите уравнение:

2 sin²x -│sin x│= 0.

Дополнительно:

1. Решите уравнение:

√3 sin x + cos x = -1

2. Решите уравнение:

2 cos²x+ cos x - 1 ≤ 0.

3. Решите неравенство:

5 sin x - 6 cos x= 6.

Группа №2

Консультация первого уровня.

1. а) Воспользуйтесь тождеством ctgx = 1/(tgx). Решается уравнение заменой переменной. При решении дробного уравнения вспомните алгоритм его решения.

б) Имеем однородное уравнение второй степени, решаем его деление обеих частей уравнения на cos x (или sin x). Затем сведем к решению квадратного уравнения.

2. Запишем решение неравенства для (π/2 + x), затем относительно “x”.

3. Решите систему способом подстановки, для этого из 1-го уравнения выразите одну переменную через другую и подставьте во второе уравнение. Решение тригонометрического уравнения записывается точками единичной окружности.

4. Помним, что верно равенство x² =│x│² для любого x. Введите замену │sinx│= y. Решение сведется к решению квадратного (неполного) уравнения.

Консультация второго уровня.

1. а) Получив дробное уравнение y + (1/y) = 2. Умножив обе части уравнения на общий знаменатель y ≠ 0. Решаем квадратное уравнениеy² - 2y+ 1 = 0. Проверьте корни уравнения. Сделайте обратную подстановку.

б) Введем новую переменную tg x= y, получаем 2y² + 5y- 7 = 0, решив его будем иметь tg x= 1, или tg x= -3,5. Решим каждое из уравнений.

2. Имеем: -(5π/6) + 2πn < π/2 + x < (7π/6) + 2πn, n ∈Z.

Найдем x.

3. Получаем: x = π/2 - y, тогда sin y = -1/2. y₁ и y₂ запишем точками единичной окружности. Затем найдем x₁ и x₂. Ответ запишем парами чисел (x₁;y₁)  (x₂;y₂)

4. Имеем: 2y² - y = 0

y = 0 или y = 1/2

Решаем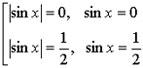   

sin x = -(1/2)

Решаем каждое из полученных уравнений относительно x.

Консультации для дополнительных заданий первого уровня.

1. Умножьте обе части уравнения на 1/2.

2. Введите замену: cos x = y и решите квадратное неравенство.

3. Воспользуйтесь формулами sin x = 2 sin(x/2)cos(x/2)

cos x + 1 = 2cos²(x/2)

Консультации для дополнительных заданий второго уровня.

1. Заметим, что (√3/2)= cos(π/6);   1/2 = sin(π/6). Имеем формулу sin(π/6 + x) в левой части уравнения. Решаем уравнение: sin(π/6 + x) = -(1/2)

2. Имеем: 2y2 + y– 1 ≤ 0

y ∈ [-1; 1/2]

-1 ≤ cos x ≤1/2

Решаем графически на единичной окружности.

3. Имеем

5 sin x - 6 cos x - 6 = 0

5 sin x - 6(cosx + 1) = 0

10 sin(x/2)cos(x/2) - 6 ∙ 2cos²(x/2) = 0

Вынесем общий множитель за скобки. Будем решать совокупность уравнений:

cos(x/2) = 0  или sin(x/2) - 1,2cos(x/2) = 0        

(имеем однородное уравнение I степени)

cos(x/2) ≠ 0.

Ответы для группы №1

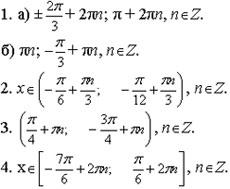
Ответы к дополнительной части.

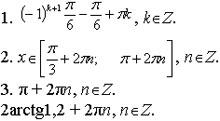
Ответы для группы №2

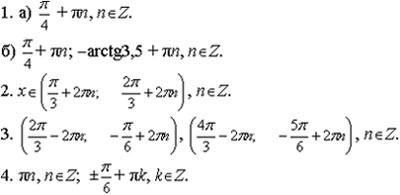
Ответы к дополнительной части.

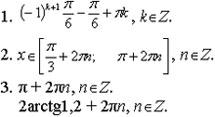
В это время группа более сильных учащихся на доске должна решить следующее задание

Решите уравнение: 

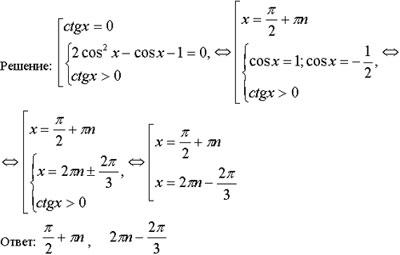
V. Угадай слово (Приложение 4)

И на последок еще такое задание, в котором всего одно слово, но какое?! Решив задания вы его и отгадаете. На доске находите карточку со своим ответом и переворачиваете ее.

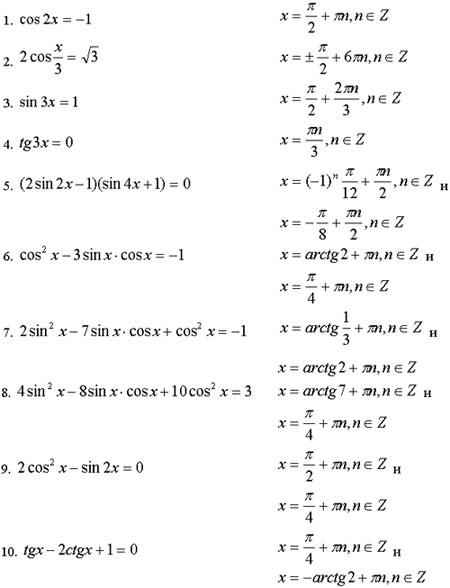
V. Подведение итогов. Домашнее задание.

Определение

Рассмотрим окружность радиуса R с центром в точке O. Положительный угол AOKсоздан вращением радиус-вектора OA (|OA| = R) по направлению против часовой стрелки.

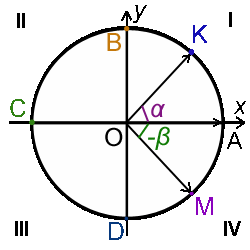
Угол 1° (1 градус) - это угол, который опирается на дугу, которая равна ¹/₃₆₀ части окружности. На рисунке выше угол ∠ AOK = α°, ∠ AOB = 90°, ∠ AOC = 180°, ∠ AOD = 270°, ∠ AOA = 360°. Вся окружность делится на 360°, один градус содержит в себе 60 минут (60'), одна минута содержит в себе 60 секунд (60").

Осями координат окружность делится на четыре четверти. Отрицательные углы откладываем от оси Ox в направлении движения часовой стрелки (на рисунке выше ∠AOM = -β° - отрицательный угол).

Кроме градусного измерения угла используется измерения угла в радианах: 1 рад - это угол, который опирается на дугу, длина которой равна радиусу. Поскольку длина окружности равна 2πR, то угол 360° = 2π рад. Исходя из этого

1 рад = ^360°/_2π = 57°17'44",

1° = ^2π/_360° рад = ^π/_180° рад.

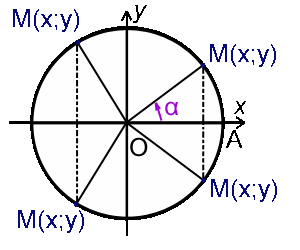
На окружности радиуса R выберем произвольную точку M(x; y), ∠ AOM = α, |OM| = R(см. рисунок выше). Определим тригонометрические функции угла α - синус (sin α), косинус (cos α), тангенс (tg α) и котангенс (ctg α):

sin α = ^y/_R, cos α = ^x/_R, tg α = ^y/_x, ctg α = ^x/_y.

Аналогично определяем тригонометрические функции произвольного угла (независимо от положения точки M она может находится в любой четверти I, II, III или IV).

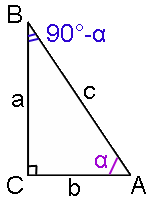
В прямоугольном треугольнике определим тригонометрически функции следующим образом:

sin α = ^a/_c, cos α = ^b/_c, tg α = ^a/_b, ctg α = ^b/_a,

где a - катет, лежащий напротив угла α, b - катет, прилегающий к углу α, c - гипотенуза.

Определим знаки тригонометрических функций у разных четвертях:

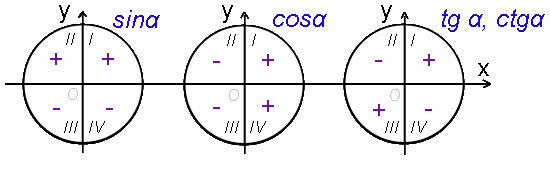
Связь между тригонометрическими функциями одного аргумента:

1. sin² α + cos² α = 1;

2. tg α · ctg α = 1;

3. 1 + tg² α = ¹/_cos² _α; 1 + ctg² α = ¹/_sin² _α;

4. sin (π - α) = cos α; cos (π - α) = sin α

Формулы суммы и разности.

1. cos (α + β) = cos α · cos β - sin α · sin β;

2. cos (α - β) = cos α · cos β + sin α · sin β;

3. sin (α + β) = sin α · cos β + cos α · sin β;

4. sin (α - β) = sin α · cos β - cos α · sin β;

5. tg (α + β) = ^{(tg α + tg β)}/_{(1 - tg α · tg β)};

6. tg (α - β) = ^{(tg α - tg β)}/_{(1 + tg α · tg β)}.

Формулы для функций двойного, тройного углов.

1. sin 2α = 2 sin α · cos α = ^{2tg α}/_{(1 + tg}² _α);

2. cos 2α = cos² α - sin² α = 2cos² α - 1 = ^{(1 - tg2 α)}/_{(1 + tg}² _α);

3. tg 2α = ^{2tg α}/_{(1 - tg}² _α);

4. sin 3α = sin α (3 - 4sin² α);

5. cos 3α = cos α (4 cos² α - 3);

6. tg 3α = ^{(3tg α - tg3 α)}/_{(1 - 3tg}² _α).

Формулы преобразования суммы и разности в произведение.

1. cos α + cos β = 2cos^{(α + β)}/₂ · cos^{(α - β)}/₂;

2. cos α - cos β = -2sin^{(α + β)}/₂ · sin^{(α - β)}/₂;

3. sin α + sin β = 2sin^{(α + β)}/₂ · cos^{(α - β)}/₂;

4. sin α - sin β = 2cos^{(α + β)}/₂ · sin^{(α - β)}/₂;

5. tg α + tg β = ^{sin(α + β)}/_{cos α · cos β};

6. tg α - tg β = ^{sin(α - β)}/_{cos α · cos β}.

Формулы преобразования произведения в сумму.

1. cos α · cos β = ½ [cos(α - β) + cos(α + β)];

2. sin α · sin β = ½ [cos(α - β) - cos(α + β)];

3. sin α · cos β = ½ [sin(α + β) + sin(α - β)].

Решить уравнение cos2x = 1/2.

__________________________

Используем метод решения простейших тригонометрических уравнений и получаем:

2x = ±arccos(1/2) + 2πn = ±π/3 + 2πn (здесь и далее, n ∈ Z).

Откуда x = ±π/6 + πn.

Ответ: x = ±π/6 + πn.

 

Решить уравнение sin(3 - 2x) = -1/2.

________________________________

Используем формулу из методов решений, имеем:

3 - 2x = (-1)ⁿ(arcsin(-1/2)) + πn = (-1)ⁿ(-π/6) + πn (здесь и далее n ∈ Z).

Делаем преобразование и получаем x = 3/2 + π/12(-1)ⁿ - πn/2.

Ответ: x = 3/2 + π/12(-1)ⁿ - πn/2.

 

Решить уравнение sin3x = π/3.

___________________________

Отметим, что π/3 > 1, а потому указанное уравнение решение не имеет.

Ответ: решений нет.

 

Найти решения уравнения sinπ(x - 3) = 0 на промежутке (-2; 6).

______________________________________________________

Пользуясь соответствующей формулой, находим:

π(x - 3) = πn (здесь и далее n ∈ Z).

x = n + 3.

Таким образом x ∈ Z и, из условия, x ∈ (-2; 6), поэтому x ∈ {-1; 0; 1; 2; 3; 4; 5}.

Ответ: x ∈ {-1; 0; 1; 2; 3; 4; 5}.

Решение тригонометрических уравнений.

1. Простейшие тригонометрические уравнения (вида f(x) = a).

sin x = a (|a| ≤ 1)   ⇒   x = (-1)ⁿ arcsin a + πn, n ∈ Z.

cos x = a (|a| ≤ 1)   ⇒   x = ± arccos a + 2πn, n ∈ Z.

tg x = a (a ∈ R)   ⇒   x = arctg a + πn, n ∈ Z.

ctg x = a (a ∈ R)   ⇒   x = arcctg a + πn, n ∈ Z.

2. Способ замены.

Этот способ следует применять в том случае, когда после преобразований получаем некое алгебраическое уравнения относительно тригонометрической функции.

Уравнение вида a(sin x + cos x) + b sin 2x = c решаем, используя замену sin x + cos x = t. Тогда 1 + sin 2x = t², а уравнение после замены приобретает вид

at + b(t² - 1) = c.

3. Разложение на множители.

Некоторые уравнения можно преобразовать так, что слева будет произведение, а справа - ноль. После чего необходимо каждый множитель приравнять к нулю и найти всевозможные корни уравнения.

4. Однородные тригонометрические уравнения вида

a₀(cos x)ⁿ + a₁(cos x)^{n - 1}sin x + ... + a_{n - 1}cos x(sin x)^{n - 1} + a_n(sin x)ⁿ = 0, n ∈ N, a₀ ≠ 0.

Для его решения необходимо поделить уравнение на (sin x)ⁿ ≠ 0 (т.к. sin x, cos xодновременно не равны 0). После чего вводим замену ctg x = z и получаем алгебраическое уравнение

a₀zⁿ + a₁z^{n - 1} + ... + a_{n - 1}z + a_n = 0, n ∈ N, a₀ ≠ 0.

5. Универсальная замена.

При решении некоторых уравнений (например, asinx + bcosx = c, a, b, c ∈ R) имеет смысл использовать замену tg ^x/₂ = z. После чего sin x = ^2z/_{(1 + z}²₎, cos x = ^{(1 - z2)}/_{(1 + z}²₎, tg x= ^2z/_{(1 - z}²₎. Так как tg ^x/₂ не определен при x = π + 2πn, n ∈ Z, то эта подстановка может привести к потери корней. Потому необходимо проверять, не являются ли числа вида x = π + 2πn, n ∈ Z корнями исходного уравнения.

Решение тригонометрических неравенств.

Простейшие тригонометрические уравнения (вида f(x) > a, f(x) < a)

sin x < a   ⇒

π(2n - 1) - arcsin a < x < arcsin a + 2πn, при a ∈ (-1;1] (n ∈ N);

x ∈ R, при a > 1;

x ∈ ∅, при a ≤ -1.

sin x > a   ⇒

2nπ + arcsin a < x < π(2n + 1) - arcsin a, при a ∈ [-1;1) (n ∈ N);

x ∈ R, при a < -1;

x ∈ ∅, при a ≥ -1.

cos x < a   ⇒

2πn + arccos a < x < 2π(n + 1) - arccos a, при a ∈ (-1;1] (n ∈ N);

x ∈ R, при a > 1;

x ∈ ∅, при a ≤ -1.

cos x > a   ⇒

2πn - arccos a < x < 2πn + arccos a, при a ∈ [-1;1) (n ∈ N);

x ∈ R, при a < -1;

x ∈ ∅, при a ≥ 1.

tg x < a   ⇒

πn - ^π/₂ < x < πn + arctg a, при a ∈ R (n ∈ N);

tg x > a   ⇒

πn + arctg a < x < πn + ^π/₂, при a ∈ R (n ∈ N);

сtg x < a   ⇒

πn + arсctg a < x < π(n + 1), при a ∈ R (n ∈ N);

сtg x > a   ⇒

πn < x < πn + arсctg a, при a ∈ R (n ∈ N);