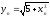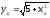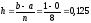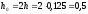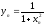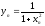Пункт 3. Метод трапеций.

Если функцию на каждом из частичных отрезков аппроксимировать (приближать) прямой, проходящей через конечные значения, то получим метод трапеций.

Площадь трапеции на каждом отрезке:

Погрешность аппроксимации на каждом отрезке:

где

Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:

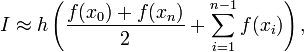где .

Погрешность формулы трапеций:

где .

Точное значение погрешности:

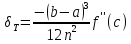, где .

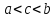Пример 12.

Вычислить интеграл при n=10 с точностью до 0,0001 по формуле трапеций.

Решение:

Разделим интервал интегрирования [0; 1] на 10 равных частей 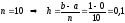шаг разбиения.

Найдем точки деления х_n и значения подынтегральной функции в этих точках.

n	xn
0	0	2.2136
1	0.1	2.2363
2	0.2	2.2378
3	0.3	2.2421
4	0.4	2.2503
5	0.5	2.2638
6	0.6	2.2839
7	0.7	2.3115
8	0.8	2.3478
9	0.9	2.3935
10	1.0	2.4494

Используя формулу трапеций, получаем

.

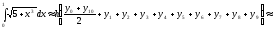
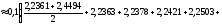
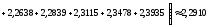Для нахождения абсолютной погрешности формулы трапеции вычислим наибольшее значение второй производной в интервале [0; 1].

;

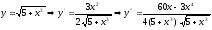
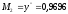тогда абсолютная погрешность Rn приближения равна:

.

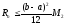
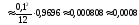Ответ:

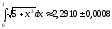
Пункт 4. Метод парабол (метод Симпсона).

Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид

.

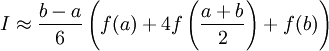Если разбить интервал интегрирования на 2N равных частей, то имеем

Погрешность формулы парабол:

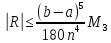, где .

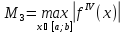Точное значение погрешности:

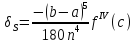, где .

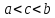Увеличение точности.

Если отыскание четвертой производной подынтегральной функции затруднено, то для оценки интеграла по формуле Симпсона можно применить метод удвоения шага вычислений, для чего:

1. удваивают шаг интегрирования;

2. вычисляют значения подынтегральной функции y=f(x) в новых точках деления;

3. используют формулу Симпсона и вычисляют ;

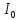4. определяют относительную погрешность, используя формулу .

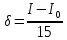Пример 13.

Вычислить интегра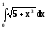л при n=10 с точностью до 0,0001 по формуле Симпсона (формуле парабол).

Решение:

Разделим интервал интегрирования [0; 1] на 10 равных частей 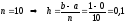шаг разбиения.

Найдем точки деления х_n и значения подынтегральной функции 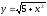в этих точках.

n	xn
0	0	2.2136
1	0.1	2.2363
2	0.2	2.2378
3	0.3	2.2421
4	0.4	2.2503
5	0.5	2.2638
6	0.6	2.2839
7	0.7	2.3115
8	0.8	2.3478
9	0.9	2.3935
10	1.0	2.4494

Используя формулу Симпсона, получаем

.

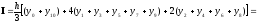
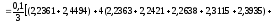
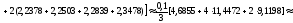
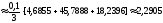Для нахождения абсолютной погрешности формулы трапеции вычислим наибольшее значение четвертой производной в интервале [0; 1].

.

;

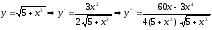
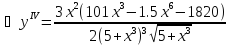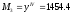тогда абсолютная погрешность Rn приближения равна:

.

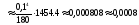Ответ:

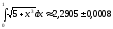
Пример 14.

Вычислить по формуле Симпсона интеграл 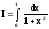, приняв n=8 и ε=0,000001.

Оценить погрешность полученного результата, пользуясь методом удвоения шага вычислений.

Решение:

Разделим интервал [0;1] интегрирования на 8 равных частей 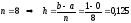- шаг разбиения.

n	xn		n		xn
0	0	1,000 000	0		0	1,000 000
1	0,125	0,984 625	-
2	0,250	0,941 176	1		0,250	0,941 176
3	0,375	0,876 712	-
4	0,500	0,800 000	2		0,500	0,800 000
5	0,625	0,719 101	-
6	0,750	0,640 000	3		0,750	0,640 000
7	0,875	0,566 389	-
8	1,000	0,500 000	4		1,000	0,500 000
 вычисляют I				 вычисляют Io

Используя формулу Симпсона 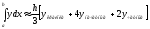, получаем

;

.

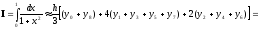
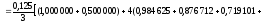
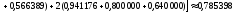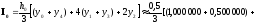
Вычислим точное значение погрешности:

.

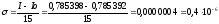Таким образом, все шесть знаков I должны быть точными.

Ответ: .
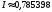