
- •Примеры:
- •Лемма. Образ и ядро линейного оператора φ являются соответственно подпространствами w и V.
- •Вычисление собственных векторов через главные миноры
- •Билинейные функции.
- •Афинное система координат.
- •Линии и поверхности.
- •Аффинная класификация кривых и поврехностей 2-го порядка.
- •Линейные преобразования унитарного простарнства.
- •Комплексификация евклидова пространства.
- •Ортогональная классификация кривых и поверхностей 2-го порядка.
Линейные преобразования унитарного простарнства.
Связь линейных преобразований и билинейных функций в унитарном пространстве.
![]() V – унитарное пространство.
V – унитарное пространство.
Ф(V)- мн-во всех линейных преобразований.
F(V) – мн-во всех билинейных преобразований.
(1) (φx,y)=f(x,y) – отображение пары чисел x, y в число
Лемма 1. Формула (1) задает биекцию множествава Ф(V) на множество F(V).
Д-во: Докажем, что
f(x,y)![]() F(V).
Ясно, что (1) есть отображение VxV→F.
Докажем, его линейность по обоим
аргументам.
F(V).
Ясно, что (1) есть отображение VxV→F.
Докажем, его линейность по обоим
аргументам.
![]()
![]()
![]() =
=
=![]()
Аналогично (даже проще) доказывается линейность по второму аргументу.
Докажем, что (1) биективное отображение.
1) Разным преобразованиям соответствуют разные билинейные функции:
![]()
![]() -
неверно =>единственность.
-
неверно =>единственность.
2) Разным бил. функциям соответствуют разные линейные функции
![]()
Пусть V -
n-мерное унитарное пространство.
![]() - ортонормированный базис.
- ортонормированный базис.
Рассмотрим матрицу
билинейной функции [f]![]()
Пусть
![]() .
Докажем, что
.
Докажем, что
![]()
![]()
![]()
![]()
Следствие. Если
выполнено (1) и
![]() - ортонормированный базис пространства
V, то выполняется (1’)
- ортонормированный базис пространства
V, то выполняется (1’)
![]()
Лемма 2. (2)
![]() - биекция мн-ва Ф(V) на мн-во
F(V)
- биекция мн-ва Ф(V) на мн-во
F(V)
Док-во: Докажем линейность по второму аргументу:
![]()
![]()
2). Аналогично доказательству Леммы 1.
3).
![]() - ортонормированный
- ортонормированный
(2’)
![]()
![]()
Следствие. Если
выполено (2) и
![]() ортонормированный базис, то выполняется
(2’)
ортонормированный базис, то выполняется
(2’)
Теорема.
![]()
(3)
![]()
Д-во:
![]() - ортонормированный
- ортонормированный
![]()
Свойства операции *:
1).
![]()
2).
![]() - тождественное
- тождественное
3).
![]()
4).
![]()
5).
![]()
6).
![]()
7). Если существует
обратное для
![]() преобразование:
преобразование:
![]()
Д-во некоторых свойств:
3).
![]()
![]()
![]()
![]()
6).
![]()
![]()
![]()
![]()
7).
![]()
![]()
О.
![]() наз. нормальным, если
наз. нормальным, если
![]() (
(![]() )
)
φ – самосопряженное
(симметрическое, эрмитовое), если
![]() .
.
φ – унитарное
(ортогональное), если
![]() .
(
.
(![]() )
)
Лемма 1. Если
![]() ,
инвариантное относительно
,
инвариантное относительно
![]() ,
то
,
то
![]() инвариантно относительно
инвариантно относительно
![]() ,
и обратно.
,
и обратно.
Д-во:
1)
![]()
![]()
![]() :
:
![]() ортогонально любому
ортогонально любому
![]()
2) Пусть
![]()
![]() - это доказано в п. 1
- это доказано в п. 1
![]()
Лемма 2. Если x
– общий собственный вектор для
![]() и
и
![]() :
:
![]() ,
тогда
,
тогда
![]()
Док-во:
![]() ;
;
![]()
![]()
Лемма 3. Если
![]() ,
тогда (f,g)=0;
,
тогда (f,g)=0;
Док-во:
![]() ;
;
![]() (f,g)=0;
(f,g)=0;
Лемма. Если V
– линейное пространство и
![]() ,
тогда у них существует общий собственный
вектор.
,
тогда у них существует общий собственный
вектор.
Док-во:
Φe=λe (e![]() 0)
0)
Рассмотрим систему
![]() такую, что система из первых m
векторов линейно независима, а система
из m+1 – линейно зависима.
Такое m существует, т.к.
пространство конечномерно, e
– линейно независимо. Ясно, что
бесконечного числа линейно независимых
векторов не бывает (их не больше dimV).
такую, что система из первых m
векторов линейно независима, а система
из m+1 – линейно зависима.
Такое m существует, т.к.
пространство конечномерно, e
– линейно независимо. Ясно, что
бесконечного числа линейно независимых
векторов не бывает (их не больше dimV).
Пусть
![]()
![]() ,
где f – собств. вектор
преобр.
,
где f – собств. вектор
преобр.
![]()
![]()
![]()
Легко доказать по
индукции, что φψ![]() =ψ
=ψ![]() φ
(i=0,..,m-1)
φ
(i=0,..,m-1)
![]()
Т.о. f – собственный вектор и преобразования φ
Теорема о нормальном преобразовании (над С).
![]() если
если
![]() - ортонормированный базис из собств.
векторов преобр.
- ортонормированный базис из собств.
векторов преобр.
![]()
Док-во: 1).![]()
![]()
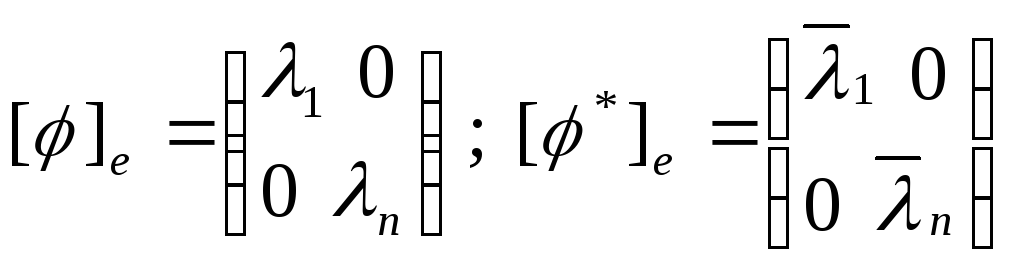 - в ортнормированном базисе.
- в ортнормированном базисе.
Тогда
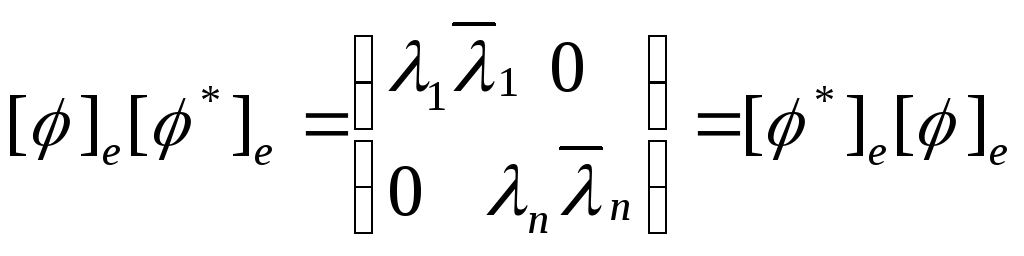
2).
![]()
Индукция по dimV. Пусть верно для n-1, докажем истинность для n.
По Лемме
![]() и он является общим собств. вектором:
и он является общим собств. вектором:
![]()
В унитарном простр-ве любую ортонормированную систему можно дополнить до ортонормированного базиса:
![]()
![]() ;
;
![]()
По Лемме 1
![]() инвариантно относительно
инвариантно относительно
![]() и относительно
и относительно
![]() ,
т.к.
,
т.к.
![]() инвариантно относительно
инвариантно относительно
![]() и
и
![]() .
.
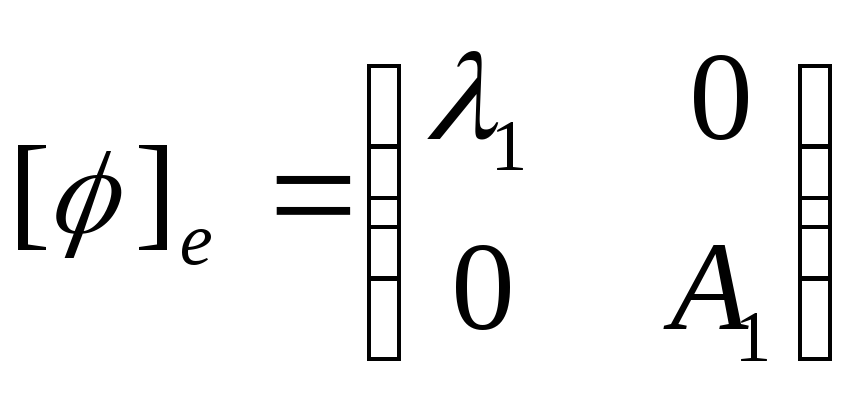
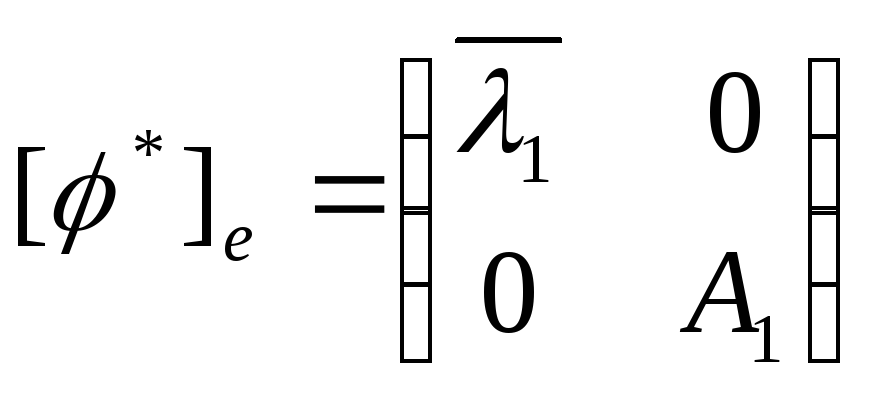
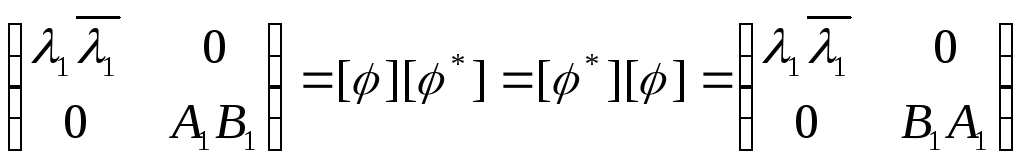 => A
=> A![]() B
B![]() =B
=B![]() A
A![]()
φ![]() - такое преобразование, матрица
которого A
- такое преобразование, матрица
которого A![]() ,
φ
,
φ![]() x=φx,
если x из V
x=φx,
если x из V![]() ,
т.е. φ
,
т.е. φ![]() - сужение преобразования φ
- сужение преобразования φ
ψ![]() - такое преобразование, матрица которого
В
- такое преобразование, матрица которого
В![]() ,
ψ
,
ψ![]() - сужение преобразования
- сужение преобразования
![]()
Но A![]() B
B![]() =B
=B![]() A
A![]() => φ
=> φ![]()
![]() =φ
=φ![]() ψ
ψ![]() =ψ
=ψ![]() φ
φ![]() =
=![]() φ
φ![]()
Т.о. φ![]() - нормальное преобразование
подпространства V
- нормальное преобразование
подпространства V![]() .
.
По предположению
индукции для φ![]() сущестсвует ортномированный базис из
собственных векторов. Возьмем его и
вектор е
сущестсвует ортномированный базис из
собственных векторов. Возьмем его и
вектор е![]() .
Эта система и будет базисом
.
Эта система и будет базисом
Следствие
1. Если φ – нормальное
преобразование унитарного пространства
V, то V=Ker(φ-λ![]() ε)
ε)![]() ..
..
![]() Ker(φ-λ
Ker(φ-λ![]() ε),
где λ
ε),
где λ![]() ,..,
λ
,..,
λ![]() суть все различные собственные числа
преобразования φ.
суть все различные собственные числа
преобразования φ.
Д-во:
Преобразование φ нормальное , значит
существует ортонормированный базис из
собственных векторов. Выберем из них
вектора соответствующие собственному
числу λ![]() .
Их d
.
Их d![]() .
Заметим, что для нормального преобразования
геометрические кратности равны
алгебраическим, иначе бы φ было бы не
диагонализируем, но нормальное всегда
диагонализируемо (из теоремы).
.
Заметим, что для нормального преобразования
геометрические кратности равны
алгебраическим, иначе бы φ было бы не
диагонализируем, но нормальное всегда
диагонализируемо (из теоремы).
Делаем так для остальных
собственных чисел. Для каждого числа
получим свой (!) базис,
т.к. сумма сосбтвенных подпространств
– прямая. И все вектора мы разобрали
т.к. d![]() +..+d
+..+d![]() =n
=n![]() +..+n
+..+n![]() =n.
Мы получим базисы ядер, причем они
ортогональны между собой, значит сумма
– ортогональная.
=n.
Мы получим базисы ядер, причем они
ортогональны между собой, значит сумма
– ортогональная.
Следствие
2. W инвариантно
относительно φ, то оно инвариантно
относительно
![]() ,
если φ – нормальное преобразование.
,
если φ – нормальное преобразование.
Д-во: φ – нормальное, тогда существует ортонормированный базис из собственных векторов. Получим:
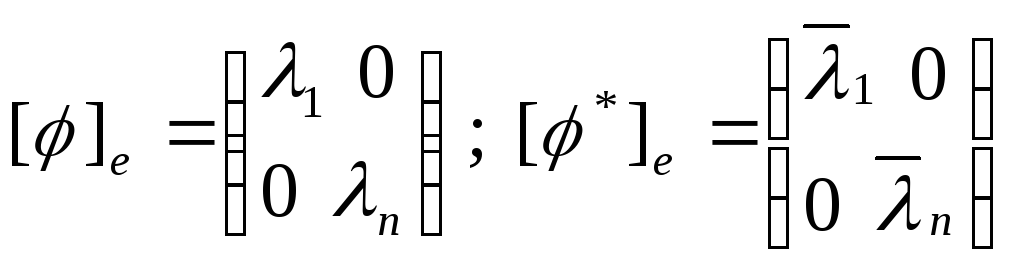 А из матрицы сопряженного преобразования
видно, что W инвариантно
относительно
А из матрицы сопряженного преобразования
видно, что W инвариантно
относительно
![]() ,
т.к. поле комплексное.
,
т.к. поле комплексное.
Следствие 3. Если φψ – нормальное преобразование и φψ=ψφ, то для φ и ψ существует общий ортонормированный базис из собственных векторов.
Унитарное преобразование.
-
Обратное к унитарному преобразованию есть унитарное преобразование.
-
Произведение двух унитарных преобразований унитарно.
Теорема об унитарных преобразованиях. Семь утверждений эквивалентны:
-
(φx,φx)=(x,x)
-
(φx,φy)=(x,y)
-
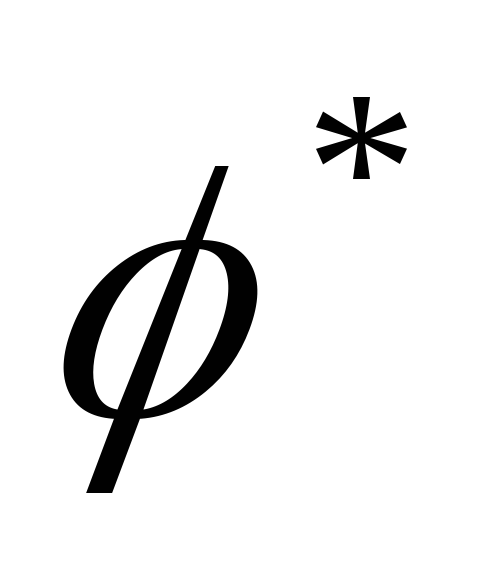 φ=ε=φ
φ=ε=φ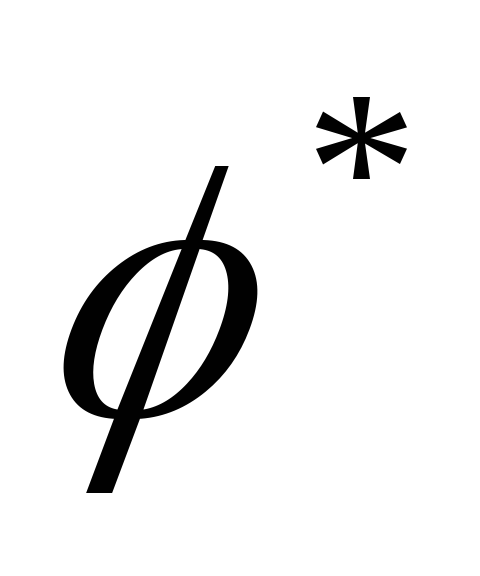
-
Для любого ортонормированого базиса
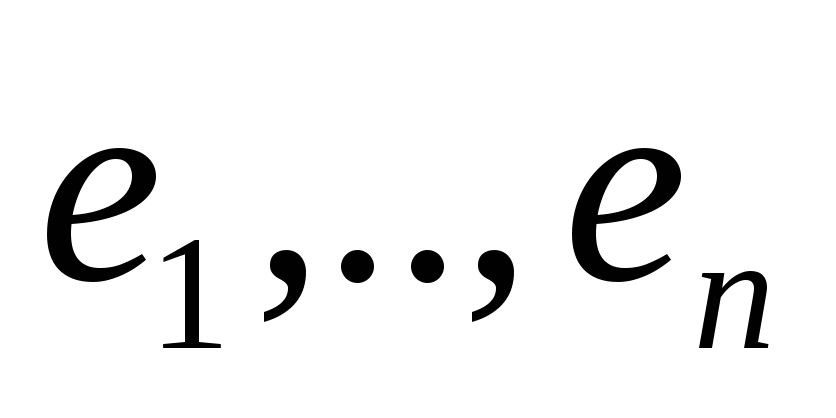 [
[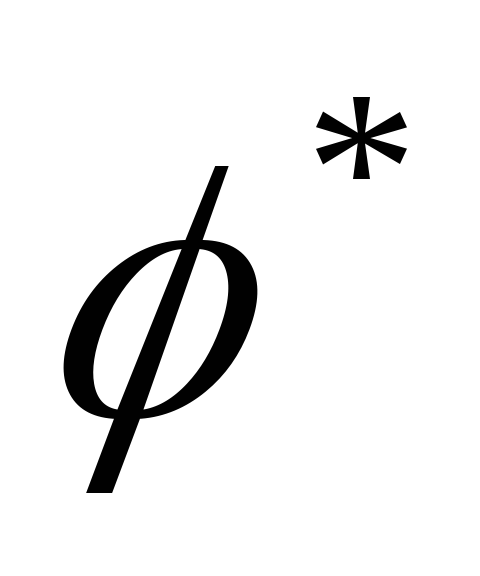 ][φ]=E=[φ][
][φ]=E=[φ][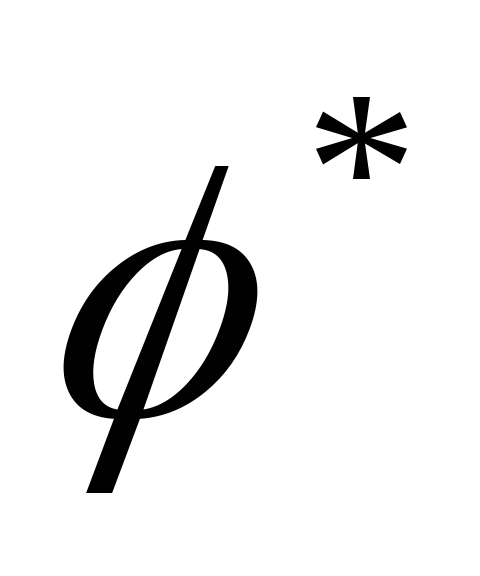 ]
] -
Для любого ортнормированного базиса
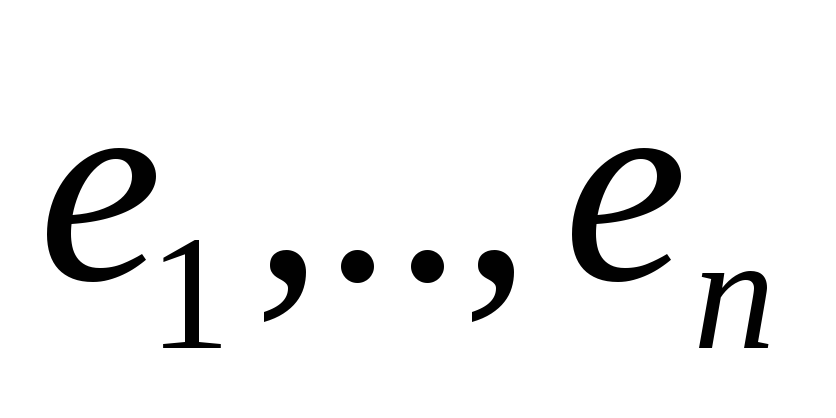
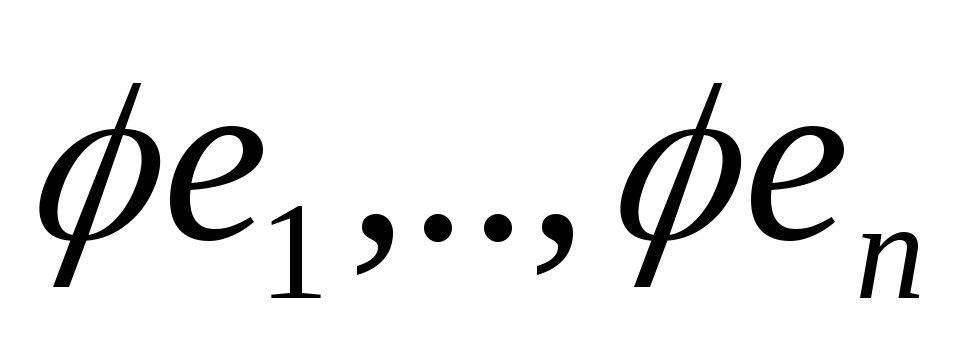 -
ортонормированны
-
ортонормированны -
Существует ортонормированный базис
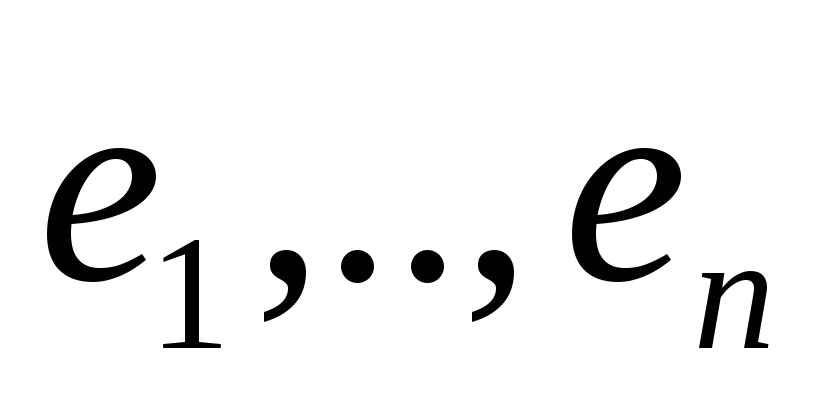 ,
что
,
что
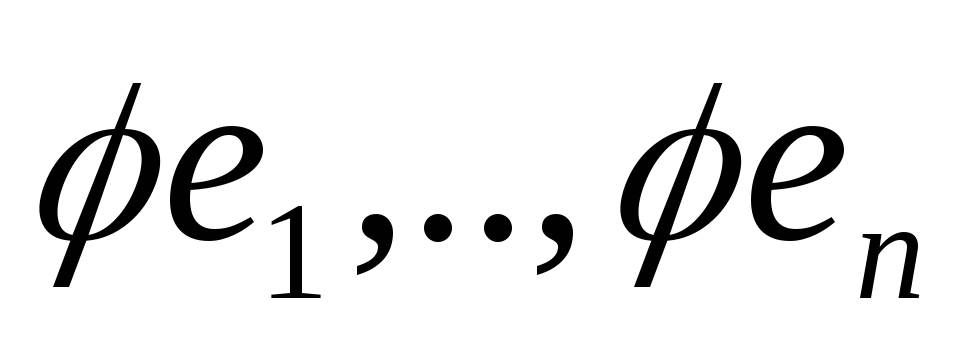 -
ортонормированны
-
ортонормированны -
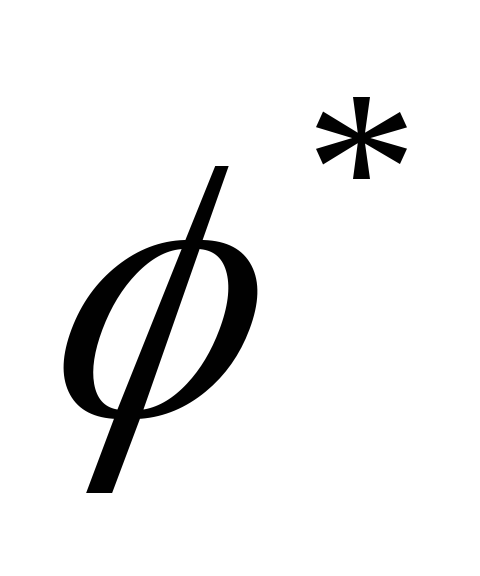 φ=φ
φ=φ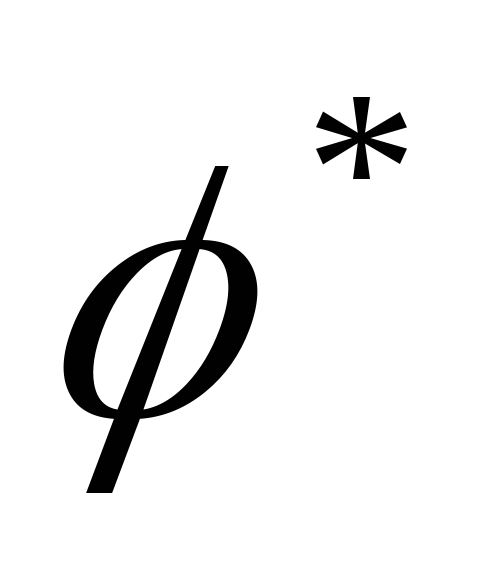 и |λ
и |λ |=1
|=1
Д-во:
1→2 y=x
2→3
(x,y)=(φx,φy)=(x,![]() φy)
=>
φy)
=>
![]() φ=ε
(х≠0)
φ=ε
(х≠0)
3→4
![]() φ=φ
φ=φ![]() => [
=> [![]() ][φ]=[φ][
][φ]=[φ][![]() ],
],
![]() φ=ε
=>[
φ=ε
=>[![]() ][φ]=E
][φ]=E
3→5
![]() - ортонормированная система =>
(φe
- ортонормированная система =>
(φe![]() ,φe
,φe![]() )=(e
)=(e![]() ,e
,e![]() )
=>
)
=>
![]() -ортонормированны.
-ортонормированны.
5→6 очевидно
6→7 (a![]() ,a
,a![]() )=(φa
)=(φa![]() ,φa
,φa![]() )=λ
)=λ![]()
![]() (a
(a![]() ,a
,a![]() )
=> |λ
)
=> |λ![]() |=1
a
|=1
a![]() - собственный вектор для λ
- собственный вектор для λ![]()
(e![]() ,e
,e![]() )=(φe
)=(φe![]() ,φe
,φe![]() )=(e
)=(e![]() ,
,![]() φe
φe![]() )
=>
)
=>
![]() φ=ε
φ=ε
7→1 Преобразование φ
нормально, тогда по теореме существует
базис из собственных векторов. В нем
[φ]=diag(λ![]() ,..,
λ
,..,
λ![]() ),
[
),
[![]() ]=diag(
]=diag(![]() )
. А так как |λ
)
. А так как |λ![]() |=1,
то [φ] [
|=1,
то [φ] [![]() ]=E.
]=E.
Следствие
4. AA![]() =A
=A![]() A
тогда и только тогда, когда существует
унитарная матрица U (UU
A
тогда и только тогда, когда существует
унитарная матрица U (UU![]() =E)
такая, что U
=E)
такая, что U![]() AU=D
из сосбтвенных чисел матрицы А.
AU=D
из сосбтвенных чисел матрицы А.
Д-во:
-
=>
Пусть φ – такое
преобразование, матрица которого А. Так
как AA![]() =A
=A![]() A,
то φ – нормальное преобразование. По
теореме о нормальном преобразовании
существует ортонормированный базис из
собственных векторов. В этом базисе
матрица A’ будет диагональной, а по
диагонали собственные числа. Осталось
доказать, что матрица перехода U
будет унитарной.
A,
то φ – нормальное преобразование. По
теореме о нормальном преобразовании
существует ортонормированный базис из
собственных векторов. В этом базисе
матрица A’ будет диагональной, а по
диагонали собственные числа. Осталось
доказать, что матрица перехода U
будет унитарной.
Самосопряженные преобразования.
Теорема. φ=φ![]() тогда
и только тогда, когда φφ
тогда
и только тогда, когда φφ![]() =φ
=φ![]() φ
и собственные числа вещественные.
φ
и собственные числа вещественные.
Д-во:
-
=> Пусть сосбтвенному числу λ соответствует вектор х, тогда
λ(x,x)=(φx,x)=(x,φx)=![]() (x,x)
=> λ=
(x,x)
=> λ=![]() => λ – вещественное.
=> λ – вещественное.
-
<= Так как φ нормальное, то существует ортонормированный базис из собственных векторов. [φ]=diag(λ
 ,..,
λ
,..,
λ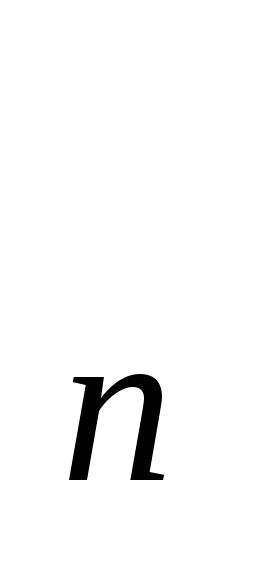 )=[φ
)=[φ ]
=> φ=φ
]
=> φ=φ
