§5. Анализ общей задачи принятия решений.

Анализ общей задачи принятия решения проведем, используя дерево решения.

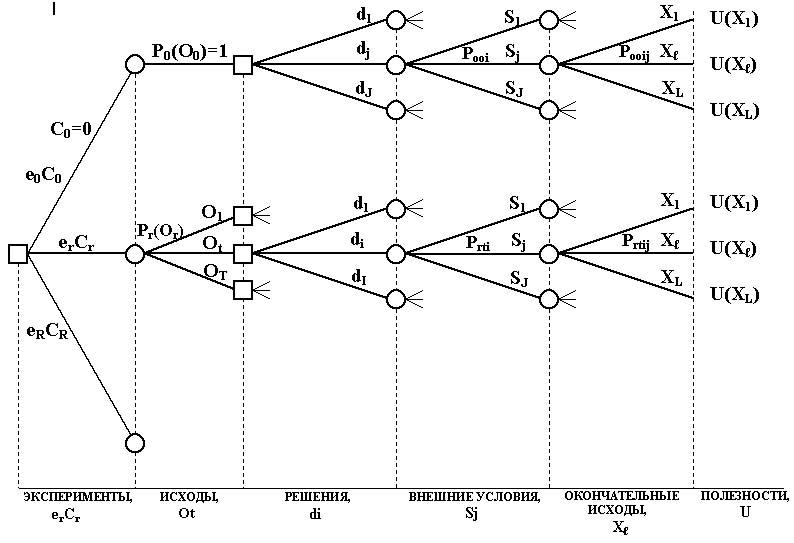
Обозначим:

U_rtij –ожидаемая полезность проведения эксперимента e_r при наблюдаемом исходе О_t, выбранном решении d_i и внешних условиях S_j.

Тогда: ,

где - означает суммирование или интегрирование по х соответственно для дискретных или непрерывных задач.

U_rti – ожидаемая полезность эксперимента e_r наблюдаемого исхода О_t и выбранном решении d_i. Тогда :

В узле решений выбирается то решение d_i, которое приводит к максимизации ожидаемой полезности:

Сделав еще один шаг в обратном направлении (с право на лево) получим выражение U_r для ожидаемой полезности выбранного эксперимента e_r:

Таким образом, наилучшим является эксперимент e_r*, который позволяет получить максимальное значение ожидаемой полезности

Поскольку любую задачу принятия решения можно представить последовательностью узлов решения и узлов возможностей, то описанная выше процедура вычисления ожидаемых полезности в узлах возможностей и максимизация ожидаемой полезности в узлах решения дает схему решения любой задачи принятий решения.

Замечание:

Если окажется что r*=0, т.е оптимальным является эксперимент е₀, то лучше всего экспериментов не проводить.

Если окажется что r*≠0, то надо сравнить полезность с затратами на этот эксперимент и тогда уже принимать решение какой эксперимент проводить и проводить ли его вообще.

§6. Экспертная оценка вероятностных распределений. Субъективные вероятности.

Аксиома 5 говорит о принципиальной возможности оценить вероятность любого события Е (P(E)), влияющего на исходы.

Обычно Р(Е) называют субъективными вероятностями.

В зависимости от того какой информацией владеет или может получить ЛПР существуют разные способы оценки вероятности Р(Е).

Рассмотрим 3 различных случая:

1

n

i=1

. Вероятности, основанные на многократном повторении случайных экспериментов.

Из теории вероятности известно, что если в результате опыта появилось nсобытий Е₁, Е₂,…, Е_n, то они составляют полную группу событий.

В опыте с равновозможными исходами все вероятности .

Вероятность любого события равна , где а – число исходов, благоприятствующих событию А,b– общее число исходов.

ЗБЧ (в формуле Бернулли) говорит о том, что

2. Оценочные суждения экспертов о вероятностях одиночных событий и о неизвестном распределении вероятности случайных величин.

Допустим нас интересует событие Е и ему приписана некоторая субъективная вероятность Р(Е), величина которой пока не определена.

Вопрос: как оценить эту вероятность.

Ответ: путем экспертного опроса.

Техника опроса: Строится 2 лотереи L₁=(x*,P,x⁰) иL₂, которая имеет исход х^*, если событие Е произошло и она имеет исход х⁰, если событие Е не произошло.

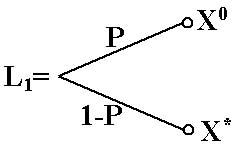
При фиксированном Р эксперту задается вопрос какая лотерея предпочтительней или равноценна.

Если ответ эксперта таков: L₁>L₂, то величину Р уменьшают и снова задают тот же вопрос.

Если ответ будет L₂>L₁, то величину Р увеличивают и снова повторяют вопрос, и так до тех пор, пока при каком-нибудь Р=Рне достигнем случая, чтоL₁иL₂равноценны (L₁=L₂), и тогда принимают Р(Е)=Р.

Так же оценивают и полную группу событий.

Аналогичный прием применяют при получении субъективных оценок неизвестной функции распределения непрерывной случайной величины. Только речь здесь идет об оценках квантилей. 100q% квантиль непрерывной случайной величины ζ(-кси)- это такое значение х_q, что вероятность того, случайная величина примет значение Р(x_q)=q.

Если q=0,5, x_0,5=медианае;

Если q=0,25 х_0,25-нижний квантиль; q=0,75 х_0,75-верхний квантиль.

F_(x)=P(x) – функция распределения случайной величины.

Общая схема оценки функции распределения такова:

Эксперту называется число q, а он должен указать х_q(квантиль). То есть: qx_q(?).

Например, для оценки медианы эксперту задают вопрос при каком значении Х равновероятно, что случайная величина Х_0,5, какое значение Х разделит интервал на равновероятные части. Таким образом, мы осуществляем последовательную дихотомию. В результате для отдельных значений функций распределенияF(x), мы получим субъективные (экспертные) оценки аргументов. Нанеся полученные точки на график, мы можем подобрать соответствующую кривую – график функцииF(x).

Следовательно, строим график F(x).

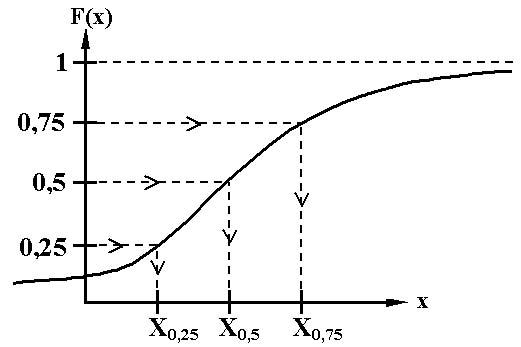- метод дихотомии.

3

n

i=1

. Байесовский подход.

Иногда для уточнения субъективных вероятностей удается использовать совместно с экспертными суждениями имеющуюся статистику в виде выборок из генеральной совокупности, такой подход основан на теореме Байеса и называется байесовским подходом.

Пусть с некоторым экспериментом связана полная группа событий (гипотез) H₁, Н₂,…, Н_n, (Н_i,H_j=иij),

Обозначим через А произвольное событие, тогда согласно теореме, имеет место следующая формула: 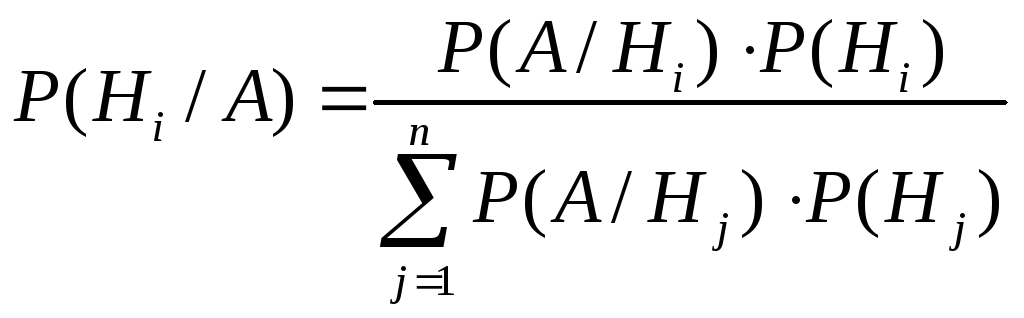, которая называетсяформулой Байеса.

P(H_i) - априорные вероятности гипотез;

Р(Н_i/А) - апостериорные вероятности гипотез;

Р(А/Н_i)-условная вероятность события А при условии наступления события Н_i.

Пример:Из урны содержащейnшаров, среди которых часть шаров белых, а часть черных (хотя черных может и не быть) наугад вынимается один шар, он оказался белым. Какова вероятность того, что всеnшаров в урне белые.

Решение: H_i– гипотеза состоящая в том, что в урнеiбелых шаров (); А – событие состоящее в том, что наугад вынут белый шар.

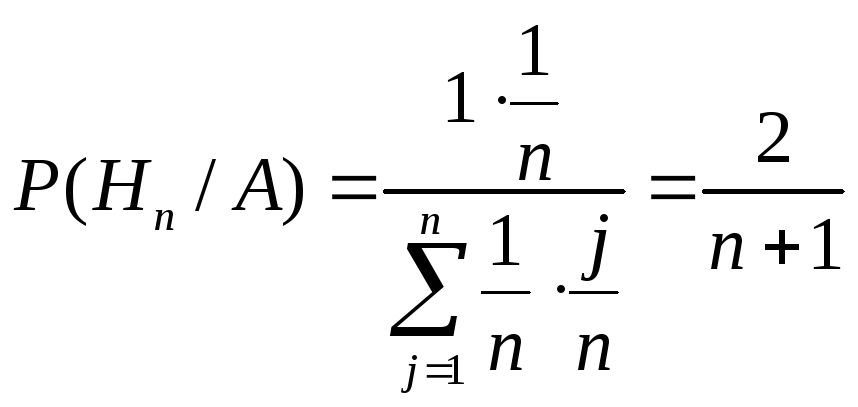
Пусть nвелико, тогда приnдостаточно большом, то есть субъективная вероятность увеличилась примерно в 2 раза.

Вернемся к оценке экспертом субъективной вероятности. Допустим, мы с помощью эксперта получили оценку, субъективную вероятность некоторого события Е, и в дальнейшем нам удалось получить какую-то информационную выборку, связанную с тем же экспериментом, в котором может появиться событие Е, тогда с учетом информации S, заключенной в информационной выборке мы можем по формуле Байеса пересчитать и уточнить Р(Е).