
Metodicheskie_rekomendatsii_k_vypolneniyu_KR_1
.pdf
7. Собственные значения и собственные векторы матрицы.
Рассмотрим квадратную матрицу Anxn и вектор-столбец
x |
|
|
0 |
|
1 |
|
|
|
|
X = x2 |
|
≠ |
0 |
. |
|
|
|
... |
|
... |
|
|||
|
|
|
0 |
|
xn |
|
|
|
|
Вектор X называется собственным вектором матрицы А, если существует такое действительное число λ ≠ 0 , что выполняется равенство
AX = λX . |
(4) |
Число λ называется собственным значением или собственным чис-
лом матрицы А.
Решим матричное уравнение
AX = λX;
AX − λX =O ;
(A − λE ) X = O.
Чтобы полученное уравнение имело ненулевое решение, необходимо,
чтобы матрица A − λE была вырожденной т.е. |
|
A − λE = 0 . |
(5) |
Уравнение (5) называется характеристическим уравнением.
Из уравнения (5) находят собственные значения. Подставляя их в уравнение (4), находят собственные векторы матрицы А.
Пример 11. Найти собственные числа и собственные векторы матри-
8 |
5 |
3 |
|
|
|
0 |
2 |
−6 |
|
цы A = |
. |
|||
|
0 |
−1 |
1 |
|
|
|
|||
Решение. Запишем матрицу A − λE . |
|
|
|
|
|
|
|
|
|
||||||||
|
8 |
5 3 |
|
|
1 0 0 |
8 |
5 3 |
λ 0 0 |
|
|
|||||||
|
0 |
2 −6 |
|
|
|
0 |
1 0 |
|
|
0 2 −6 |
|
|
0 λ 0 |
|
= |
||
A − λE = |
|
− λ |
|
= |
|
− |
|
||||||||||
|
0 |
−1 1 |
|
|
|
0 |
0 1 |
|
|
0 |
|
−1 1 |
|
|
0 0 λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
8 |
− |
λ |
5 |
|
|
3 |
|
|
|
|
|
|
|
|
|
= |
|
0 |
|
2 − λ |
|
−6 |
|
|
|
|
|
|
|||
|
|
|
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
−1 |
|
1− λ |
|
|
|
|
|
|||
Составим характеристическое уравнение: |
|
|
|
|
|
|
|||||||||||
|
|
|
8 − λ |
|
5 |
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
2 − λ |
|
−6 |
= 0; |
|
|
|
|
|
||
|
|
|
|
0 |
|
|
−1 |
|
1− λ |
|
|
|
|
|
|
|
|
31
|
8 − λ |
5 |
3 |
|
|
( |
|
) |
|
(( |
|
|
) |
( |
|
) |
|
) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
2 − λ −6 |
|
|
8 − λ |
|
2 − λ |
|
− 6 |
|
|||||||||
|
|
= |
|
|
|
|
|
1− λ |
|
|
= |
||||||||
|
0 |
−1 |
1− λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (8 − λ) (2 −3λ + λ2 − 6)= (8 − λ) (λ2 −3λ − 4)= 0. |
|||||||||||||||||||
Решим полученное уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
(8 − λ) (λ2 −3λ − 4)= 0; |
|
|
|
|
|
|
||||||||||
|
λ = 8 или λ2 −3λ − 4 = 0; λ |
= −1; λ |
= 4. |
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
λ1 = 8 , λ2 = −1, λ3 = 4 – собственные значения матрицы А.
Для каждого из полученных собственных значений найдем собствен-
ные векторы матрицы А. |
|
|
|
|
|
8 −8 |
5 |
|
3 |
0 |
5 3 |
|
2 − |
8 |
|
|
|
1) Если λ = 8 , то A − λE = 0 |
−6 |
= 0 |
−6 −6 |
||
0 |
−1 |
1−8 |
0 |
−1 −7 |
|
и матричное уравнение выглядит: |
|
|
|
|
|
|||
0 |
5 |
3 |
x |
|
|
0 |
|
|
|
0 |
−6 |
−6 |
1 |
|
|
0 |
|
|
x2 |
|
= |
. |
||||
|
0 |
−1 |
−7 |
|
|
|
0 |
|
|
x3 |
|
|
|
||||
Этому уравнению соответствует однородная система линейных урав-
5x2 + 3x3 = 0;
нений −6x2 − 6x3 = 0;
−x2 −7x3 = 0.
Из второго уравнения x2 = −x3 , тогда оставшиеся два уравнения будут
иметь вид: |
|
|
|
|
|
|
|
|
|
|
|
||
−5x |
3 |
+ 3x |
3 |
= 0; |
|
−2x |
3 |
= 0; |
x |
|
= 0, x |
|
= 0, x = m, m , m ≠ 0. |
|
|
|
|
|
3 |
2 |
|||||||
x3 −7x3 = 0; |
|
−6x3 = 0; |
|
|
1 |
||||||||
|
|
|
|
|
|
||||||||
m
Тогда вектор X1 = 0
0
, m , m ≠ 0 – собственный вектор матрицы А.
8 +1 |
5 |
3 |
|
9 5 3 |
|
|||
|
0 |
2 +1 |
−6 |
|
|
0 |
3 −6 |
|
2) Если λ = −1, то A − λE = |
|
= |
|
|||||
|
0 |
−1 |
1+ |
|
|
0 |
−1 2 |
|
|
1 |
|
|
|||||
32
и матричное уравнение выглядит: |
|
|
|
|
|
|||
9 |
5 |
3 |
x |
|
|
0 |
|
|
|
0 3 |
−6 |
1 |
|
|
0 |
|
|
|
x2 |
|
= |
. |
||||
|
0 |
−1 2 |
|
|
|
0 |
|
|
|
x3 |
|
|
|
||||
Этому уравнению соответствует однородная система линейных урав-
9x + 5x |
2 |
+ 3x |
3 |
= 0; |
||
|
1 |
|
|
|
||
нений |
|
3x2 |
− 6x3 |
= 0; |
||
|
|
− x2 |
+ 2x3 = 0. |
|||
|
|
|||||
Очевидно, что система содержит два одинаковых уравнения: второе и
9x + 5x |
|
+ 3x |
|
= 0; |
||
третье, поэтому ее можно переписать в виде: |
1 |
|
2 |
|
3 |
|
|
|
− x2 + 2x3 = 0. |
||||
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9x |
+ 5x |
|
+ 3x |
|
= 0; |
|
9x |
+10x |
|
+ 3x |
|
= 0; |
x |
= −13 x |
; |
|||
|
1 |
|
2 |
|
3 |
|
|
1 |
|
3 |
|
3 |
|
1 |
9 |
3 |
|
|
|
|
− x2 + 2x3 = 0; |
|
x2 |
= 2x3; |
|
|
|
|
x2 = 2x3; |
|
|
||||||
|
|
|
|
x3 = 9k, x2 =18k, x1 = −13k, k , k ≠ 0. |
|
|
|
|||||||||||
|
|
|
|
|
−13k |
|
|
|
|
|
|
|
|
|
|
|
||
Тогда вектор X2 = |
18k , k |
, k ≠ 0 – собственный вектор матрицы А. |
||||||||||||||||
|
|
|
|
|
|
9k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 − 4 |
|
5 |
|
|
3 |
4 |
5 3 |
|||||
|
|
0 |
|
2 − 4 |
|
−6 |
|
|
0 |
−2 −6 |
|
||
3) Если λ = 4 , то A − λE = |
|
|
|
= |
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
0 |
−1 −3 |
|
|
|
|
−1 1− 4 |
|
|||||||||
и матричное уравнение выглядит: |
|
|
|
|
|
|
|
|
|
|
|
||
4 |
5 |
3 |
x |
|
|
0 |
|
|
|
|
|
||
|
0 |
−2 |
−6 |
1 |
|
= |
|
0 |
|
|
|
|
|
|
x2 |
|
|
. |
|
|
|
|
|||||
|
0 |
−1 |
−3 |
|
|
|
|
0 |
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
||||
Этому уравнению соответствует однородная система линейных урав-
4x + 5x |
2 |
+ 3x |
3 |
= 0; |
||
|
1 |
|
|
|
||
нений |
|
− 2x2 |
− 6x3 |
= 0; |
||
|
|
− x2 |
−3x3 |
= 0. |
||
|
|
|||||
Очевидно, что система содержит два одинаковых уравнения: второе и
4x + 5x |
|
+ 3x |
|
= 0; |
||
третье, поэтому ее можно переписать в виде: |
1 |
|
2 |
|
3 |
|
|
|
− x2 |
−3x3 |
= 0. |
||
33

Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x + 5x |
|
+ 3x |
|
= 0; |
|
4x −15x |
|
+ 3x |
|
= 0; |
|
x = 3x |
; |
|||||||
|
1 |
|
2 |
|
3 |
|
|
|
1 |
|
|
3 |
|
3 |
|
1 |
3 |
|
||
|
|
− x2 −3x3 = 0; |
|
x2 |
= −3x3; |
|
|
|
|
x2 = −3x3; |
||||||||||
|
|
|
|
x3 = t, x2 = −3t, x1 = 3t, t , t ≠ 0. |
|
|
|
|||||||||||||
|
|
|
|
|
3t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда вектор X3 = |
−3t , t |
, t ≠ 0 – собственный вектор матрицы А. |
||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
−13k |
|
3t |
|
|
|
|
|
|
||||||||
Ответ: X1 |
= |
0 |
, X |
2 |
= |
|
18k |
, X3 |
= |
−3t , m,k,t |
, m ≠ 0,k ≠ 0, t ≠ 0. |
|||||||||
|
|
|
0 |
|
|
|
|
9k |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аналитическая геометрия
8. Векторы в 2 u 3. Скалярное произведение векторов.
Вектором называют направленный отрезок или упорядоченную пару (тройку) чисел. Векторы, параллельные одной прямой или лежащие на прямой, называются коллинеарными. Векторы, лежащие в одной плоскости или параллельные одной и той же плоскости, называются компла-
нарными.
Проекцией вектора AB на ось Ox называется длина отрезка CD этой оси, заключенного между основаниями перпендикуляров, прове-
денных из начальной и конечной точек вектора AB , взятая со знаком плюс, если направление отрезка CD совпадает с направлением оси проекции (рис. 2), и со знаком минус, если эти направления противоположны (рис. 3).
|
|
B |
|
|
B |
|
|
A |
|
α |
|
|
|
α |
|
|
x |
|
|
A |
x |
||
0 C |
|
|
|
|
|||
|
D |
0 |
D |
C |
|||
|
|
|
|||||
|
Рисунок 2 |
|
|
|
Рисунок 3 |
|
|
Проекция вектора на ось равна длине вектора, умноженной на косинус угла между вектором и осью:
прOx AB =| AB | cosα.
Проекции вектора на координатные оси называются координатами
вектора: a = (x;y;z); AB = (xB − xA;yB − yA;zB − zA ).
Линейными операциями над векторами называют сложение и вычи-
тание векторов, умножение вектора на постоянное число.
34

Если векторы a и b заданы своими координатами a = (x1;y1;z1),
b = (x2;y2;z2 ), то a ± b = (x1 ± x2;y1 ± y2;z1 ± z2 ).
При умножении вектора на число все его координаты умножаются на это число.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
a b =| a | | b | cosϕ; a b =| a | прab =| b | прba.
Отметим, что a b = 0 тогда и только тогда, когда векторы перпендикулярны или хотя бы один из них нуль-вектор.
Из формулы скалярного произведения векторов легко получить формулу для определения угла между векторами:
cosϕ = |
a b |
. |
|
||
|
| a | | b | |
|
Если векторы a и b заданы |
своими координатами a = (x1;y1;z1), |
|
b = (x2;y2;z2 ), то их скалярное произведение равно сумме произведений одноименных координат:
a b = x1x2 + y1y2 + z1z2.
Если вектор a задан своими координатами a = (x1;y1;z1), то его длину можно найти по формуле:
a = x12 + y12 + z12 .
Механический смысл скалярного произведения. Если материаль-
ная точка, на которую действует сила F , совершает перемещение вдоль вектора s , то работа А силы равна скалярному произведению вектора силы на вектор перемещения: A = F s.
9. Векторное произведение векторов.
Упорядоченная тройка некомпланарных векторов с общим началом называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого вектора ко второму виден в направлении, противоположном направлению движения часовой стрелки. В противном случае тройка векторов называется левой.
Векторным произведением вектора a на вектор b называется век-
тор a ×b , длина которого численно равна площади параллелограмма, построенного на этих векторах | a ×b |=| a | | b | sinα , который перпенди-
кулярен плоскости векторов a и b и направлен так, чтобы тройка векторов a, b, a ×b была правой.
Отметим, что a ×b = 0 тогда и только тогда, когда векторы коллинеарны или хотя бы один из них нуль-вектор.
35

Если векторы a и b заданы своими координатами a = (x1;y1;z1), b = (x2;y2;z2 ), то их векторное произведение равно
|
i |
j |
k |
|
a ×b = |
x1 |
y1 |
z1 |
. |
|
x2 |
y2 |
z2 |
|
Механический смысл векторного произведения. Пусть некоторое твердое тело неподвижно закреплено в точке А, а в точке В этого тела приложена сила F . В этом случае возникает вращающий момент, численно равный произведению | AB | | F | sinα. В механике его принято
называть моментом силы: M = AB ×F .
10. Смешанное произведение трех векторов.
Смешанным произведением трех векторов называется число, которое получится, если первые два вектора перемножить векторно и результат скалярно умножить на третий вектор: (a ×b) c = a b c .
Отметим, что смешанное произведение векторов a b c = 0 тогда и
только тогда, когда векторы компланарны или хотя бы один из них нульвектор.
Смешанное произведение некомпланарных векторов a, b, c по моду-
лю численно равно объему параллелепипеда, построенного на векто- рах-сомножителях. Оно положительно, если тройка векторов правая, и отрицательно, если она левая.
Если векторы a , b и c заданы своими координатами a = (x1;y1;z1), b = (x2;y2;z2 ), c = (x3;y3;z3 ), то смешанное произведение равно опреде-
лителю
x1 y1 z1 a b c = x2 y2 z2 .
x3 y3 z3
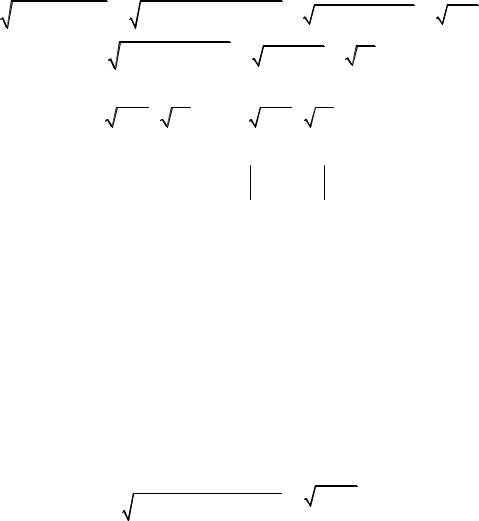
Пример 12. Даны четыре точки: A(4;7;8), B(–1;13;0), C(2;4;9), S(1;8;9).
Найти:
6)угол между ребрами AB и AS;
7)площадь грани АВС;
8)объем пирамиды SABC.
Решение.
1)Для нахождения угла между ребрами AB и AS воспользуемся форму-
лой: |
JJG |
JJJG |
|||||
JJJG JJJG |
|||||||
AB AS |
|||||||
cos ϕ = cos(AB,AS) = |
|
JJJG |
|
|
JJJG |
. |
|
|
|
AB |
|
AS |
|
||
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJG |
JJG |
||
Найдем координаты и длины векторов AB и AS : |
|||||||||||||||||||
JJJG |
|
− x |
|
; y |
|
− y |
|
; z − z |
|
) = (−1− 4; 13 −7; 0 −8) = (−5; 6; −8); |
|||||||||
AB = (x |
|
|
|
|
|
||||||||||||||
|
JJJG |
B |
|
|
|
A |
|
B |
|
|
A |
B |
A |
|
|
|
|
|
|
JJJG |
AS = (xS − xA; yS − yA; zS − zA ) = (1− 4; 8 −7; 9 − 8) = (−3; 1; 1); |
||||||||||||||||||
= x2 + y2 + z2 = |
(−5)2 + 82 +(−8)2 = |
25 |
+ 36 + 64 = 125 ≈11,180; |
||||||||||||||||
AB |
|||||||||||||||||||
|
|
|
|
JJJG |
= |
|
(−3)2 +12 +12 = |
9 +1 |
+1 = |
11 ≈ 3,317. |
|||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
AS |
|
||||||||||||||
Тогда cos ϕ = |
−5 (−3) + 6 1−8 1 |
= |
13 |
|
|
≈ 0,351. |
|||||||||||||
|
125 |
11 |
|||||||||||||||||
|
|
|
|
|
|
|
|
125 |
11 |
|
|
|
|||||||
2) Площадь грани АВС найдем по формуле:
SABC = 1 AB × AC .
JJG2
Найдем координаты вектора AC:
JJJG
AC = (xC − xA; yC − yA; zC − zA ) = (2 − 4; 4 −JJG7; 9 −JJG8) = (−2; − 3; 1) .
Найдем векторное произведение векторов AB и AC:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB × AC = |
−5 |
|
6 |
|
−8 |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
−3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= i (6 1−(−8) (−3)) − j ((−5) 1−(−8) (−2)) + k ((−5) (−3) − 6 (−2)) = |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= −18i + 21j + 27k. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда площадь грани АВС равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
SABC = |
1 |
|
AB × AC |
|
= |
|
1 |
(−18)2 + 212 |
+ 272 |
= |
|
1494 |
|
≈ 38,652 |
=19,326 (ед2 ). |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) Найдем объем пирамиды SABC: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
V = |
1 |
JJJG JJJG JJJG |
|
JJJG |
JJJG |
JJJG |
|
|
x1 |
y1 |
z1 |
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
AB AC AS |
, AB |
AC AS = |
x |
2 |
y |
2 |
z |
2 |
|
||||||||||||||||||||||
|
|
|
пир |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
JJG |
|
|
|
|
|
|
|
|
|
x3 |
y3 |
z3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= (x |
; y |
; z |
|
|
) = (−2;−3;1); |
|||||||||||||||||
|
|
|
AB = (x ; y ; z ) = (−5;6;−8) ; AC |
|
|
||||||||||||||||||||||||||||||
|
|
1 |
1 |
1 |
JJJG |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
AS = (x3; y3; z3 ) |
= (−3;1;1) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
JJJG |
|
JJJG |
JJJG |
= |
|
−5 |
|
6 |
−8 |
|
= 20 − 6 + 88 =102. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
AB AC AS |
|
−2 |
−3 |
1 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vпир = |
1 |
102 =17 (ед3 ). |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37

11. Прямая на плоскости.
Выпишем различные виды уравнения прямой L на плоскости:
1. L: Ax + By +C = 0 – общее уравнение прямой, вектор n =(A;B) перпендикулярен прямой и называется ее нормальным вектором.
2.L: A(x − x0 ) + B(y − y0 ) = 0 – уравнение прямой с нормальным вектором (A; B) , проходящей через точку M0(x0;y0 ).
3.L : ax + by =1 – уравнение прямой «в отрезках».
4. L : y = k x + b – уравнение прямой с угловым коэффициентом k = tgϕ , где ϕ – угол между прямой L и положительным направлением оси Ox.
5.L : y − y0 = k(x − x0 ) – уравнение прямой с угловым коэффициентом k = tgϕ , проходящей через точку M0(x0;y0 ).
6.L : x = x0 + mt, – параметрические уравнения прямой L, где вектор
y = y0 + nt,
s = (m;n) параллелен прямой L и называется направляющим вектором прямой, параметр t .
7. |
L : |
x − x0 |
|
= |
y − y0 |
|
|
– уравнение прямой с направляющим вектором |
|||||
|
|
|
|||||||||||
|
|
|
m |
|
|
|
n |
|
|
||||
s = (m;n) , проходящей через точку M0(x0;y0 ). |
|||||||||||||
8. |
L : |
x − x1 |
= |
y − y1 |
– уравнение прямой, проходящей через две за- |
||||||||
|
|
||||||||||||
|
|
x |
2 |
− x |
|
|
y |
2 |
− y |
1 |
|
||
|
|
|
1 |
|
|
|
|
|
|
||||
данные точки M1(x1;y1) и M2(x2;y2 ).
Углом между двумя прямыми называют угол между их нормальными векторами.
1) Пусть прямые L1 и L2 заданы общими уравнениями:
L1 : A1x + B1y +C1 = 0 , L2 : A2x + B2y +C2 = 0 , |
тогда угол между прямыми |
||||||||||||||
определяется по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosϕ = |
n1 n2 |
|
|
= |
|
|
A1A2 + B1B2 |
|
|
. |
|||||
| n1 | | n2 |
| |
|
|
|
|
|
|||||||||
|
|
|
|
A 2 |
+ B 2 |
A 2 |
+ B |
2 |
|
||||||
|
|
|
|
|
|
|
1 |
1 |
2 |
2 |
|
||||
Условие перпендикулярности этих прямых: A1A2 + B1B2 = 0 . |
|||||||||||||||
Условие параллельности: |
|
A1 |
|
= |
|
B1 |
. |
|
|
|
|
|
|||
|
A |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
B |
|
|
|
|
|
||||
|
|
2 |
|
|
|
2 |
|
|
|
|
L1 : y = k1x + b1 и |
||||
2) Пусть прямые L1 |
и |
L2 |
заданы |
уравнениями: |
|||||||||||
L2 : y = k2x + b2 , тогда угол между прямыми определяется по формуле:
tgϕ = k2 − k1 . 1+ k1k2
Условие перпендикулярности этих прямых: k1 k2 = −1.
38
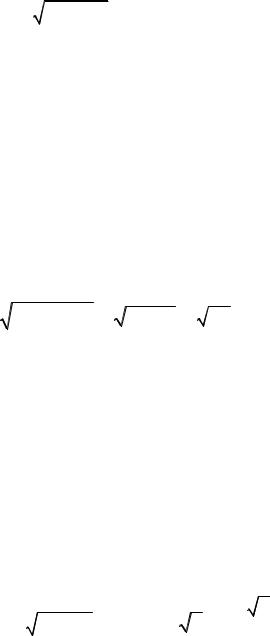
Условие параллельности: k1 = k2 .
Расстояние от точки M1(x1;y1) до прямой Ax + By +C = 0 определя- ется по формуле d = | Ax1 + By1 +C | .
Пример 13. Даны вершины треугольника АВС: А(4;3), В(–3;–3), С(2;7). Найти:
1)длину стороны АС;
2)длину высоты ВН, проведенной из вершины В;
3)уравнение высоты ВН;
4)уравнение медианы СМ, проведенной из вершины С;
5)сделать чертеж.
Решение. |
|
|
|
JJG |
||
1) Длину стороны АС найдем как длину вектора |
||||||
AC: |
||||||
JJJG |
= (xC − xA; yC |
− yA ) = (2 |
− 4; 7 −3) |
= (−2; 4); |
||
AC |
||||||
|
JJJG |
= (−2)2 + 42 = 4 +16 |
= 20 ≈ 4,472. |
|||
|
AC |
|||||
2) Для нахождения длины высоты ВН составим уравнение прямой (АС). Воспользуемся уравнением прямой, проходящей через две заданные точки A(x1;y1) и C(x2;y2 ):
(AC) : |
x − x1 |
|
= |
|
y − y1 |
|
(AC) : |
x − 4 |
= |
y −3 |
(AC) : |
x − 4 |
= |
y −3 |
. |
|||||||||||
|
|
|
|
|
|
2 − 4 |
7 −3 |
−2 |
|
|||||||||||||||||
|
x |
2 |
− x y |
2 |
− y |
1 |
|
|
|
|
4 |
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найденное уравнение прямой (АС) можно записать в виде: |
|
|
|
|||||||||||||||||||||||
(AC) : |
|
x − 4 |
= |
y −3 |
|
|
(AC) : |
x − 4 |
= |
y −3 |
(AC) : 2x + y −11 = 0. |
|||||||||||||||
|
|
−2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
−1 |
2 |
|
|
|
|
|
|
|||||||
Тогда, расстояние от точки В(–3; –3) до прямой (AC) : 2x + y −11 = 0 :
d = | 2 (−3) +1 (−3) −11| |
= |
| −20 | |
= 4 5 ≈ 8,944. |
22 +12 |
|
5 |
|
JJJG3) Высота ВН перпендикулярна прямой (АС). Следовательно, вектор AC BH и является нормальным вектором прямой (ВН). Составим урав-
нение высоты ВН, пользуясь уравнением прямой, заданной нормальным
JJJG
вектором AC = (−2; 4) , проходящей через заданную точку B(−3;−3):
(BH): − 2(x −(−3)) + 4(y −(−3)) = 0 −(x + 3) + 2(y + 3) = 0 − x + 2y + 3 = 0. 4) Найдем координаты середины отрезка АВ по формуле:
|
x |
A |
+ x |
|
y |
A |
+ y |
C |
|
|
4 |
−3 |
|
3 |
−3 |
1 |
|
|
|||
xM = |
|
C |
; |
yM = |
|
|
|
M |
|
|
; |
|
|
|
M |
|
; 0 |
. |
|||
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
39
|
y |
|
|
|
Для составления уравнения меди- |
||||||||||||
|
7 |
|
|
C |
|
||||||||||||
|
|
|
|
аны СМ воспользуемся формулой |
|||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
уравнения прямой, проходящей че- |
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
рез две точки С(2;7) и M |
2 |
; 0 |
: |
||||||||
|
3 |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
(CM): |
x − 2 |
= |
y −7 |
|
x − 2 |
= |
y −7 |
; |
|||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
H |
|
1 2 − 2 0 −7 |
−3 2 |
|
−7 |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
(CM): 14x −3y −7 = 0. |
|
|
|
|||||||
–3 |
|
0 |
|
M 1 2 |
4 |
x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
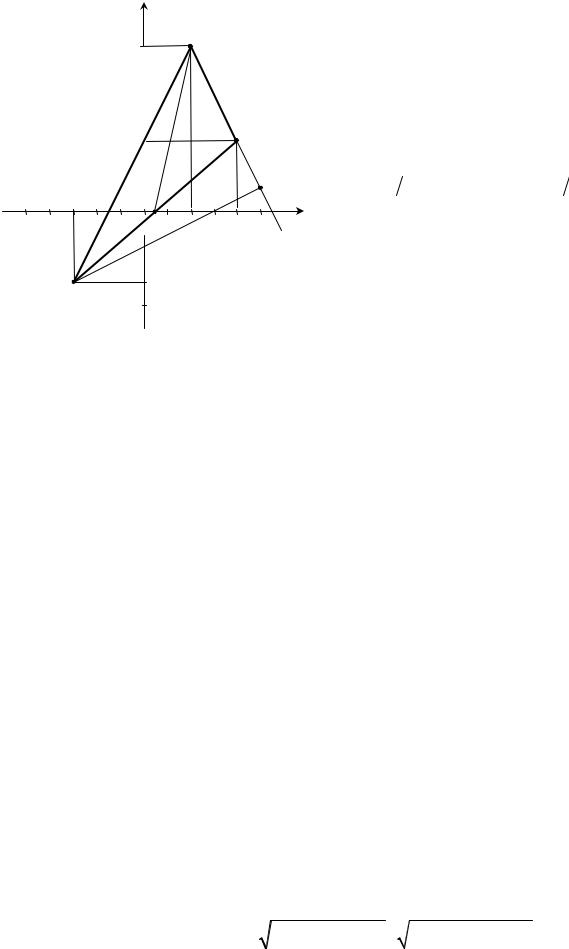
5) Решение задачи проиллюстри- |
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
руем на рис. 4. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
B |
–3 |
|
Рисунок4 |
||
|
12. Плоскость.
Общее уравнение плоскости имеет вид Ax + By +Cz + D = 0, где n = (A;B;C) называют нормальным вектором плоскости, причем выпол-
няется условие A2 + B2 +C2 ≠ 0 .
Существуют различные способы задания плоскости, выпишем соот-
ветствующие им уравнения: |
|
|
|
|
|
|
||||||||||||||||||
1. A(x − x0 ) + B(y − y0 ) +C(z − z0 ) = 0 – |
уравнение плоскости с извест- |
|||||||||||||||||||||||
ными нормальным вектором n = (A;B;C) |
и точкой M0(x0;y0;z0 ), |
принад- |
||||||||||||||||||||||
лежащей плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. |
|
|
x |
+ |
y |
+ z =1 |
– |
|
уравнение |
плоскости |
в «отрезках», |
причем |
||||||||||||
|
|
a |
|
|||||||||||||||||||||
|
|
|
|
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a ≠ 0, b ≠ 0, c ≠ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. |
|
x − x1 |
y − y1 |
|
|
|
z − z1 |
|
= 0 – уравнение плоскости, проходящей че- |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
|||||||||||||||||||||
|
|
|
x3 − x1 y3 − y1 z3 − z1 |
|
|
|
|
|
|
|
|
|||||||||||||
рез три заданные точки Mi (xi ;yi ;zi ), |
(i =1,2,3) . |
|
|
|
||||||||||||||||||||
Рассмотрим две плоскости: α: A1x + B1y +C1z + D1 = 0 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и β: A2x + B2y +C2z + D2 = 0 . |
|
|||||
Углом между двумя плоскостями α |
и β |
называется угол между их |
||||||||||||||||||||||
нормальными векторами: |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
cosϕ = |
|
|
n1 n2 |
|
= |
|
A1A2 + B1B2 +C1C2 |
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
n1 |
|
n2 |
|
|
|
A12 + B12 +C12 A22 + B22 |
+C22 |
|
||||||
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
