Metodicheskie_rekomendatsii_k_vypolneniyu_KR_1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

г) y2 cos x = sin(3x2 ) + y;

y = arcsin

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

661 Кб

Скачать

☆

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

5.19.а)

в)

5.20.а)

в)

5.21.а)

в)

5.22.а)

в)

5.23.а)

в)

5.24.а)

в)

5.25.а)

в)

5.26.а)

в)

lim

x3 +12x

12x2 + x +

x→∞

lim

19x

x→0 arctg x

lim

x2 − 4x +1

5 −3x + 4x2

x→∞

lim

4 tg5x

x→0

sin x

lim

x2 −7x +10

5x + x2

x→∞

lim

7arcsin3x ,

x→0

lim

x3 + 4x2 + 4x

12x3

+ 6x2

x→∞

lim 11sin2x ,

x→0

lim

x4 + 2x −1

x→∞ x3 −7x2 +

lim

5 tg2 x

x→0 1−cos x

lim

x2 + 3x + 5

5x2 − 4x +

x→∞

lim

8arctg3x ,

x→0

lim

x2 − 4x − 21

7x −

3x2

x→∞

lim

5sin5x ,

x→0

tg x

lim

2x3 + x +1

x3 + x2

x→∞

lim

sin2 3x

x→0

3x2

б)

lim

x2 − 21x + 38

x −18 −1

x→19

г)

lim

9x − 22 3x+3

9x +

;

x→∞

б)

lim

x2 −18x − 40

5 + x −5

x→20

г)

lim

10x − 21 4−5x

;

x→∞

10x +19

б)

lim

25 − x − 2

24x − x2 − 63

x→21

x −11 x−1

г)

lim

;

x→∞

x −10

б)

lim

x2 − 24x + 44

3 −

x −

x→22

г)

lim

2x −8 6−4x

2x +

;

x→∞

б)

lim

24 − x −1

22x − x2 + 23

x→23

г)

lim

3x + 24 5−3x

;

x→∞

3x +1

б)

lim

x +1 − 5

x→24 x2 − 23x − 24

4x +1 6x−4

г)

lim

;

x→∞

4x −5

б)

lim

625 − x2

2x −1 −

x→25

г)

lim

5x −12 2−5x

;

x→∞

5x −7

б)

lim

2x2 + x −3

2 − x −1

x→1

г)

lim

2x −1 x−1

;

2x +

x→∞

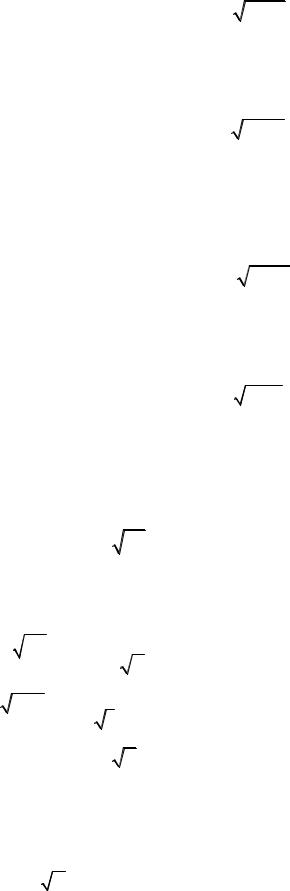
5.27.

а)

lim

x2 − x +1

, б)

lim

x − 2 −1

2x3 + 5x2 − 2

x→∞

x→2 x2 −3x +

в)

lim

arcsin6x

x −1 4−x

г)

lim

;

x→0

x→∞

x + 3

5.28.

а)

lim

2x4 + x2 +1

б)

lim

6 + x −3

x4 + x

x→∞

x→3 x2 − 2x −

в)

lim

arctg3x

x + 2 5−x

г)

lim

;

x→0

x→∞

x +1

5.29.

а)

lim

3x2 + 6x −1

б)

lim −x2 + 6x −8

x→∞

2x +1

x→4

x + 5 −3

в)

lim

tg8x

3x −1

x+3

г)

lim

;

3x −5

x→0

x→∞

5.30.

а)

lim

x3 + x −1

б)

lim

5 + 4x − x2

3x3 + x2 +1

x −1 − 2

x→∞

x→5

в)

lim

sin x

г)

lim

3x +12 6−x

;

x→0 tg5x

x→∞

3x + 7

Задание 6. В задачах 6.1.-6.30. найти производные y′x

функций:

6.1.

а) y = 2x6

−

+ x2

x3 ,

б) y = ctg5 2x arccos x2,

в) x =

y = ln(t − 2),

г)

x − y + eyarctgx = 0;

− 2

6.2.

а) y = x

−

б)

y =

arctg3 2−x

x2 + x

в) x = t −1, y =

г) y2x = ex ;

6.3.

а) y = 4x2 −

+ x5

б) y = (sin x2 +1) arctg2 2x

в) x =

cost

y =

sint

г) x4 + y4 = x2y2;

+ 2cost

+ 2sint

6.4.

а) y = x

7 −

б) y = cos3(3x) arctg(x3 ),

3 x

в) x = tgt,

y =

г) x − y2 + tg(x2y) = 0;

sin2t

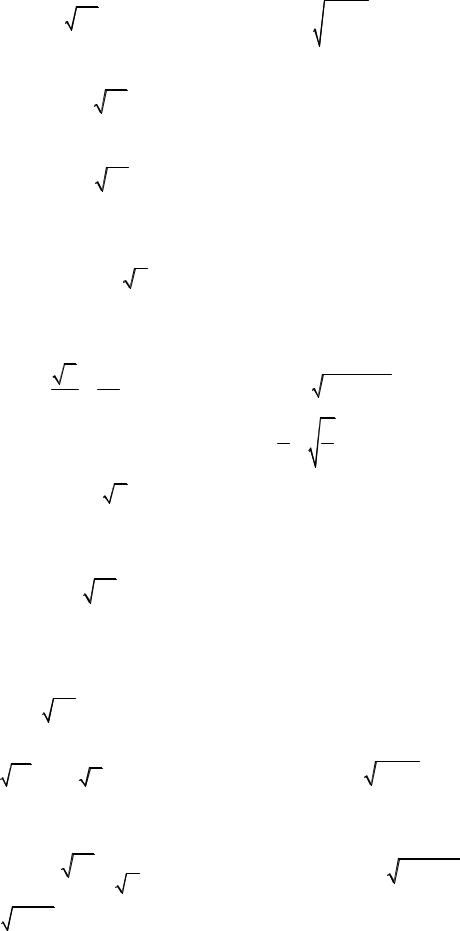
6.5.	а) y =		1	− 2x		x3 + 4x3,

			x2
	в)	x = 2(t − sint), y = 4(2 + cost),
6.6.	а)	y = x6 −			1	+ 2 6 x5 ,
					x6

	в) x = t + sint,					y = 2 + cost,

6.7.а) y = 4x3 − 2x + x3 x2 ,

в) x = cost, y = lnsint,

6.8.	а) y = 2x3 −		1	+ 2x3 x,
6.8.	а) y = 2x3 −	x3		+ 2x3 x,
		x3
	в) x = 4 − sin		πt	, y = −4cos	2	πt	,
	в) x = 4 − sin		6	, y = −4cos		6	,
			6			6

6.9.а) y = 4x3 − 7xx + x35 −5x,

в) x = 8sin

πt

y = −6cos πt

6.10.

а) y = x4 −

+ x5

πt

y = sin πt

в) x = 6 −cos

− 2,

6.11.

а) y = 7 −

+ x3 x4 + x9,

πt

y = 4 − 6cos πt

в) x = 2 −cos

6.12.

а) y = x2 −

+ 5x ,

3 x4

в) x = cost + t sint,

y = sint −t cost,

6.13.

а) y = 3 x2 +12x6 x − 4x3,

в) x = cos2t,

y =

cos2 t

6.14.

а) y = x5 + x3

x2 −

5 x

в) x = 1−t2 , y =

б)	y = 3				x −3		,

					x + 3
б) exy + x2 + y3 = 2;
б)	y = sin2(3x) −cos x3,
г) ex + ey − 2exy =1;
б)				ln(1+x2 )				x	2	,
	y = 2
г)	xe	−	1 y		+ ye	−		1 x	= 2;
			2					2
б)	y =				tg x2						,
				ln(x2 − 2x					+ 4)

г) x4 - x2y2 + y4 - 5x2 + 5y2 - 1= 0;

б) y = x4 −3x2 sin5x ,

г) yx − 3 xy = x;

б) y = lnsin2x tg(x + 2) ,

г) sin2(2x − y2 ) = 3x + 2; б) y = 2x2 sinln(x + 4),

г) x2 −3xy + y2 + x −5y = 0;

г) x3 + 3xy2 + 2y2 −5x =1;

б)	y = sin(ln x) 2x − x2 ,
г)	x	= tg(x2 − y);
	y

6.15.

а)

y =

−

+ x

x6 ,

πt

в)

x = −2cos

πt

, y =

4 − 4sin

6.16.

а)

y = x8 +

− x4

x3 ,

в)

x = sht,

y = th2t,

6.17.

а)

y = x3

x −

+ 3 ,

x x

в) x = t2 + t, y = 3 t −1,

6.18.

а)

y =

−3x3 + 2x

x7 ,

в) x = t3 −1, y = lnt,

6.19.

а) y =

x5 +

− x3 ,

3 x

в) x = t −1, y =

t −1

6.20.а) y = x2 − x52x +147 x ,

в) x = et , y = arcsint,

6.21.а) y = 2 1x3 −3x5 + 6x3 x ,

в)	x = sint,	y =			1	,
				cost

6.22. а) y = x2 −		1	+		x2		− 4 ,
		2x3
					x3
в)	x = cost + sint,				y = sin2t,

6.23.а) y = 4 − x3 x2 + x2 − x14 ,

в) x = cost, y = sin2 2t ,

6.24.а) y = 33 x2 − 2x + x−3 ,

в) x = cos2 t, y = tg2t,

б) y = ln(cos x) cos tg x ,

г) (x − y)2 + cos y2 = 4;

б)

etgx

2x +

г) x

y + y3 cos x = 3;

б) y = ex2 −3x (x2 − x),

г)

y2 = x2 − xln y + 3;

б)

y =

ctg(3x2 + 2x)

ln x

г) x2 ln y − y2 ln x =1;

б)

earcsin x

x2 +

г)

y2 =

y − x

;

x + y

б)

8arctg(x +1)

x2 − 4x + 4

г)

y2 sin x = cos(x − y);

б)

e−cos x

ctg(2 x)

г)

ln y = arctg

;

б)

= ln

−3x +1

+ 3x +1

г)

x2 + y2 = arctg

;

б)

y = sin x2 (sin2 2x −1),

г) y2 + x2 −cos(x2 y2 ) = 2;

б)	y = (sin6x − 3x) x3 − x ,
	y	= 5x +1;
г)	tg

	x

6.25.

а) y = x5 −

− x

x5 ,

б) y =

ln(x2 +1)

6x3 − 2x

= −3sin2 πt

в) x = −4 −cos πt ,

г) x2 + ey − x ln y = 0;

6.26.

а) y = x2 −

+ x3 3 x2 ,

б) y = 2ln(1+x2 ) sin x ,

в) x =

y =

г) xy = arctg

;

1−t

6.27.

а) y =

−

+ 7 x ,

б) y = arcctg(x2 +1) ex ,

3 x4

πt

в) x = 4cos πt ,

y = 9sin

− 4,

г) x4 − xy2 + y3 − 4y + 5 = 0;

6.28.

а) y =

−

+ x

б) y =

сtg(x3 + x)

2x +1

в) x = 2 −3cos

πt ,

= 9cos πt ,

г)

= arctg

;

6.29.

а) y =

− x

x −

б) y =

ln(2x −5)

2x2 −3x −

в) x = arcgt,

y = t2 ,

г) ex sin y − ey cos x =1;

6.30.

а) y = 8x12 − x5 x2 −

+ x6 ,

б) y = arctg x2 ,

x2 + 4x

в) x = cht,

−y

y = sh t,

г) ln x + e x =1.

Задание 7. В задачах 7.1.-7.30. найти уравнения касательной и нор-

мальной плоскости.
7.1.	rG = (t − sint)		i +(1− cost) Gj + 2sint kG,		t0 =	π .
	rG = 6t Gi + 3t2 Gj + t3 kG,					2
7.2.	rG = 6t Gi + 3t2 Gj + t3 kG,				t0 = 1.
7.3.	rG = 2sint Gi + 3tgt Gj + 2cos t kG,				t0 =	π .
	rG	= 3cht Gi + 3sht Gj + 3at kG,				4
7.4.	rG	= 3cht Gi + 3sht Gj + 3at kG,			t0 = 0 .
7.5.	rG	= et Gi + e−t	Gj + 2 t kG,		t0 = 0 .
7.6.	rG = 2sin2 t Gi + 2cos2 t Gj + sin2t kG,				t0 =	π .
	rG = ln(t −3) i − t Gj +(t2 −16) kG					4
7.7.	rG = ln(t −3) i − t Gj +(t2 −16) kG			,	t0 = 4 .
7.8.	rG = (2 − t) Gi +		25 − t2 Gj + t2 kG	,	t0 = 4 .

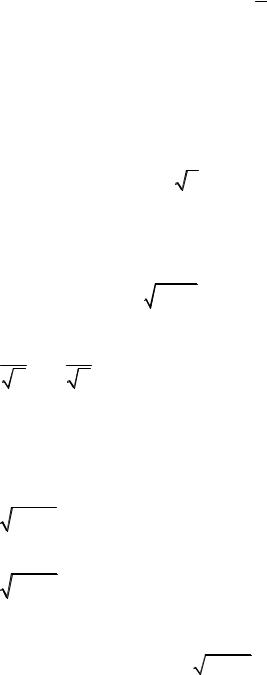
7.9.rG = et Gi +(1+ t2 ) Gj + arctgt kG,

7.10.rG = et cos t Gi + et sint Gj + et kG,

7.11.rG = (t − sint) Gi +(1− cos t) Gj + 4sin 2t kG,

7.12.rG = (t3 −3) Gi +(t2 + 2) Gj +lnt kG,

7.13.rG = (t3 + 8t) i + t2 Gj +(5t5 + 3t) kG,

7.14.rG = 2t Gi −3t Gj +lntgt kG,

7.15.rG = 4t Gi +lnt Gj + t2 kG,

7.16. rG = lncos t Gi +lnsint Gj + 2 t kG,

7.17.rG = (cos t + t sint) Gi +(sint − t cos) Gj + t kG,

7.18.rG = (t2 +1) Gi + cos t Gj + et kG,

7.19.rG = (t +1)2 Gi + t3 Gj + t2 G,

7.20.G = (3t − t3 ) i + 3t2 Gj +(3t + t2 ) kG,+1 kr

7.21.rG = t Gi + t Gj +lnsint kG,

7.22.rG = ch22t Gi + sht2 cht Gj + sh2t kG,

7.23.rG = et sint Gi + Gj + et cos t kG,

7.24.rGG = (1+ 3tG+ 2t2 ) Gi G+(2 − 2tG+ 5t2 ) Gj +(1− t2 ) kG,

7.25.r = cos t i + sint j + cht k ,

7.26.rG = 5 − t2 Gi − (2t − t2 ) Gj + (5 − 2t2 ) kG,

7.27.rG = t2 Gi +(t3 − 2) Gj + t6 kG,

7.28.rG = t3 + 3 Gi −ln(2t −1) Gj + t3 kG,

7.29.rG = 2tgt Gi + 3cos t Gj + 3sint kG,

7.30. rG = et+1 Gi −(t2 −3t +1) Gj + 2t + 6 kG,

t0 = 1. t0 = 0 .

t0 = π.

t0 = 1.

t0 = 0 . t0 = π4 .

t0 = 1. t0 = π4 . t0 = π2 .

t0 = 0 . t0 = 0 .

t0 = 1. t0 = π2 .

t0 = 0 . t0 = 0 . t0 = 1. t0 = 0 .

t0 = 1. t0 = 1.

t0 = 1. t0 = π4 . t0 = −1.

Задание 8. В задачах 8.1.-8.30. провести полное исследование указанных функций и построить их графики.

8.1.

y =

;

8.2. y =

−x2

−1

;

8.3.

y =

;

x −1

8.4.

y =

;

8.5. y =

;

8.6. y =

;

x +

− x

−x −

8.7. y =

+ 2

;

8.8. y =

−x2

− 2

;

8.9. y =

;

x − 2

8.10. y =

;

8.11. y =

;

8.12.

;

− x

+ 2

−x −

8.13.

y =

2 + 3

;

8.14. y =

−x

2 −3

;

8.15.

y =

;

+ 3

8.16. y =

;

8.17. y =

;

8.18.

y =

;

−

− x

−x −

8.19.

y =

2 + 4

;

8.20. y =

−x

2 − 4

;

8.21.

y =

;

+ 4

8.22. y =

;

8.23. y =

;

8.24.

;

−

− x

−x −

8.25.

y =

2 +1

;

8.26. y =

−2x2 −1

;

8.27.

y =

;

2x +

8.28. y

;

8.29. y =

;

8.30.

y =

−2x −

−

2x −

Рекомендации к выполнению заданий контрольной работы

Основы линейной алгебры

1. Матрицы и операции над ними.

Прямоугольная таблица, состоящая из m ×n элементов произвольной природы, называется матрицей.

Матрицы обычно обозначают прописными буквами латинского алфавита: A, B, C, … и записывают в виде

a11	a12	...	a1n		a11	a12	...	a1n
a	a	...	a	, или	a	a	...	a	, или сокращенно
A = 21	22		2n	, или	A = 21	22		2n	, или сокращенно
		...	...				...	...
... ...		...	...		... ...		...	...
am1	am2	...	amn		am1	am2	...	amn

A = (aij ), i =1,m, j =1,n .

aij называют элементами матрицы. Если элементы матрицы числа,

то матрицу называют числовой, если векторы – векторной, функции – функциональной и т.д. В дальнейшем будем рассматривать только числовые матрицы.

Элементы матрицы нумеруются двумя индексами: номер строки и номер столбца, в которых стоит элемент.

Количество строк и столбцов матрицы определяют ее размерность, т.е. если у матрицы m строк и n столбцов, то говорят, что матрица размерности m на n и записывают: Am×n .

Говорят, что две матрицы равны, если равны их размерности и соответствующие элементы этих матриц.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается О.

Матрица, состоящая из одной строки, называется матрицей строкой

или вектор-строкой, из одного столбца – матрицей столбцом или вектор-столбцом.

Матрица, у которой число строк и столбцов одинаковое, называется квадратной матрицей. Квадратную матрицу, у которой n строк называют матрицей порядка n. У квадратных матриц выделяют главную и побочную диагонали. Элементы a11, a22, a33, ...,ann образуют главную диаго-

наль, элементы a1n, a2n−1, ...,an1 – побочную диагональ.

Квадратная матрица, у которой все элементы, кроме элементов глав-

ной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной матрицей и обозначается Е.

Квадратная матрица называется треугольной, если все элементы по одну сторону от главной диагонали равны нулю. Различают верхнюю и нижнюю треугольные матрицы.

Действия над матрицами:

Транспонирование.

Замена строк матрицы соответствующими столбцами называется транспонированием. Транспонированную матрицу обозначают AT .

	1	0		1		4	−1
	4	−2	T	1		4	−1
Например, если A =	4	−2	, то A	=	0	−2	3
	−1	3			0	−2	3
	−1	3

Сложение матриц.

Суммой матриц А и В называется матрица С, каждый элемент которой


равен сумме		соответствующих								элементов матриц А и В, т.е.
cij = aij + bij , i =		1,m	, j =		1,n	.
	1 2			0 −3					1	−1
Например:				+			=	2		.
	3 4			−1 3				2		7

Заметим, что сложение может быть выполнено только для матриц с одинаковой размерностью.

Умножение матрицы на число.

Произведением матрицы А и действительного числа λ называется матрица В, каждый элемент которой равен произведению соответст-

вующего элемента матрицы А на число λ , т.е. bij = aij λ, i =1,m, j =1,n.

	1 2 0 1	3	3		6	0 3
Например:	−1 2 6 0		=	−3	6	18 0	.

Произведение матриц.

Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. Например, матрица Am×n согласована с матрицей Bn×k .

Умножение матрицы А на матрицу В может быть выполнено только тогда, когда матрица А согласована с матрицей В.

Произведением матрицы Am×n на матрицу Bn×k называется матрица Cm×k , каждый элемент которой cij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матри-

n
цы В, т.е. cij = ∑ais bsj , i =		, j =		.
цы В, т.е. cij = ∑ais bsj , i =	1,m	, j =	1,k	.
s=1
				1		−1	1		2
					0	−3	1		2
Пример 1. Найти произведение матриц A =					0	−3	и B =	3	4	.
					3	−2		3	4
					3	−2

Решение.

1 1+ (−1) 3 1 2

+ (−1) 4

−1

−2

−3

0 1+ (−3) 3 0 2

+ (−3) 4

−9

−12

−2

3 1+ (−2) 3 3 2

+ (−2) 4

−3

−2

−9

−12

Ответ:

−3

−2

Из существования произведения A B ,вообще говоря, не следует существование произведения B A . В случае, если AB = BA , матрицы А и

Вназывают перестановочными.

Возведение в степень.

Операция возведения в степень может быть выполнена только для

квадратных матриц An = A A ... A .

				n раз
1		2 2		1 2	1 2	1 1+ 2 3 1 2 + 2 4						7 10
Например:	2	4	=		3 4	=	3	1+ 4 3 3	2	+ 4 4	=	15 22
	2	4		3 4	3 4		3	1+ 4 3 3	2	+ 4 4		15 22

2. Определители.

Основной числовой характеристикой квадратной матрицы является определитель (детерминант). Определитель квадратной матрицы Anxn

обозначают: , det A , A .

Для матрицы А первого порядка определитель det A равен ее элементу a11.

Для матрицы А второго порядка определитель det A записывают в ви-

де det A = a11 a12 и вычисляют по правилу:

a21 a22

			det A =	a11	a12	= a a		−a	a .
				a21	a22	11	22	12	21
Например:	1	2	=1 4 − 2 3 = 4 − 6 = −2.
Например:	1	2	=1 4 − 2 3 = 4 − 6 = −2.
	3	4

Для матрицы А третьего порядка определитель det A записывают в

виде det A =	a11	a12 a13		и вычисляют по правилу:
виде det A =	a21	a22 a23		и вычисляют по правилу:
	a31	a32	a33
det A =		a11	a12	a13	= a11a22a33 + a12a23a31 + a21a32a13 −
		a11	a12	a13
		a21	a22	a23
		a31	a32	a33
					−a13a22a31 −a12a21a33 −a32a23a11.

Правило вычисления определителя третьего порядка называют пра-

вилом треугольника или правилом Саррюса. Это правило можно запи-

сать с помощью схемы (рис.1): со знаком «плюс» берут произведения элементов, стоящих на главной диагонали и в вершинах треугольников, основания которых параллельны главной диагонали; со знаком «минус» – произведения элементов, стоящих на побочной диагонали и в вершинах треугольников, основания которых параллельны побочной диагонали.

				Рисунок 1
Пример 2. Вычислить определитель					1	2	4	.
					1	2	4
					0	−1	2
					−3	1	4
Решение. Воспользуемся правилом Саррюса.
	1	2	4	=1 (−1) 4 + 2 2 (−3)+ 0 1 4 − 4(−1)(−3)−0 2 4 −1 2 1 =
	1	2	4
	0 −1		2
	−3	1	4
				= −4 −12 + 0 −12 −0 − 2 = −30.				Ответ: –30.

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.02.201624.06 Кб15means of communication.doc
#
18.02.20161.98 Mб10mechkovskaia.pdf
#
18.02.2016147.97 Кб4melkie_shpory.doc
#
18.02.2016136.7 Кб3Metadychka_GViT_d_.doc
#
18.02.2016371.71 Кб8metod-dipl 1.doc
#
18.02.2016661 Кб9Metodicheskie_rekomendatsii_k_vypolneniyu_KR_1.pdf
#
23.11.2019743.42 Кб6metodicheskie_ukazaniaOOP_1_chast.doc
#
17.11.2019156.16 Кб12Metodicheskie_ukazania_po_kursovomu_proektirova...doc
#
18.02.2016567.3 Кб6Metodicheskie_ukazanija.pdf
#
23.11.201973.73 Кб4metodichesk_posobie_dlya_kursovogo_proekta_po_P...doc
#
18.02.2016198.66 Кб7metodichka.doc